1 В странах со стабильной экономикой безрисковой обычно считается цен­ная бумага, выпущенная государственным казначейством.

176

Для этого заменим в портфеле бумагу К с параметрами d_y9 o_y на бумагу с такой же доходностью, но с нулевой дисперсией. До­ходность портфеля от такой замены, разумеется, не изменится. Что же касается дисперсии, то она теперь составит:

0=0*0*.

X X

Дисперсия дохода портфеля теперь зависит от удельного ве­са безрисковой составляющей, так как

Таким образом, "разбавление" портфеля безрисковой бума­гой снижает риск портфеля в целом, а квадратическое отклоне­ние дохода портфеля определяется убывающей линейной функ­цией доли безрисковой бумаги. Если d_x > d_y (в противном слу­чае проблема выбора портфеля отпадает — он должен состоять только из безрисковых бумаг), то доход от портфеля по мере увеличения доли безрисковой бумаги уменьшается от d_x до d, a величина квадратического отклонения сокращается от о_х до О (см. рис. 8.7). И наоборот, рост доли рисковой бумаги увеличи­вает как риск, так и доход.

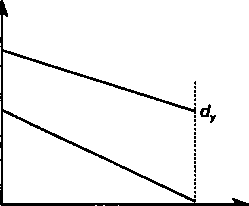
А, а d_x

О 1 а_у

Рис. 8.7

Последнее утверждение для портфеля, состоящего из двух видов бумаг, иллюстрируется уравнением (8.10), которое полу­чено преобразованием (8.7):

Л ⁼ ^⁺К~4Х- (8Л0)

В свою очередь на основе (8.9) находим

177

В итоге получим интересное соотношение

d - d А = d+— ^Lo. (8.11)

^У °х

Дробь в приведенном выражении иногда называют рыночной ценой риска. Если эта величина равна, скажем, 0,5, то при ро­сте квадратического отклонения на 1% доход увеличится на 0,5%.

§8.3. Минимизация дисперсии дохода

Приведенные выше выражения для дисперсии суммарного дохода позволяют рассмотреть проблему диверсификации инве­стиций и риска еще в одном аспекте, а именно, — определить структуру портфеля, которая минимизирует дисперсию и, сле­довательно, риск. Для нахождения минимума дисперсии вер­немся к определяющим ее формулам. Если предположить, что нет статистической зависимости между доходами от отдельных видов инвестиций, то найти оптимальную в указанном смысле структуру портфеля не так уж и сложно. Положим, что порт­фель, как и выше, состоит из двух видов бумаг Хи К Их доли в портфеле составляют а_х и 1— а# а дисперсии D_x и D_y. Общая дисперсия определяется по формуле (8.5). Поскольку эта функ­ция является непрерывной, то применим стандартный метод определения экстремума. Находим, что минимальное значение дисперсии суммы имеет место тогда, когда

Формулу (8.12) обычно приводят в аналитической финансо­вой литературе. Однако, для того, чтобы ею можно было вос­пользоваться, необходимо иметь значения дисперсий. По-види­мому, при расчетах на перспективу удобнее оценить или задать экспертным путем отношение дисперсий:

D_x/y=D_x/D_y. (8.13)

178

Разделим теперь числитель и знаменатель (8.12) на D_y, полу­чим

_ъ-тттт- ⁽⁸¹⁴⁾

х/у

При наличии корреляции между показателями доходов обра­тимся к (8.6). Минимум этой функции имеет место в случае, когда

D — г о о

°^х D +D -2г оо^{9 ( }}

х у *'ху х у

или, использовав отношение дисперсий (8.13), получим

^l-^rxyjDx/y ,_й -,.

а_х " т—. (8.16)

&х/у ⁺ * " 2^гхуу&х/у

Как видно из приведенных формул, расчетная величина до­ли одной из бумаг может при некоторых условиях оказаться от­рицательной. Отсюда следует, что этот вид бумаги просто не должен включаться в портфель.

ПРИМЕР 8.2. Вернемся к данным примера 8.1 и определим стру­ктуру портфеля с минимальной дисперсией. Напомним, что о_х = 0,8; о_у= 1,1.

При полной положительной корреляции расчетные значения доли первой бумаги составят по формуле (8.15)

1,1²-1 х 0,8x1,1 *^х 0,8²+ 1,1²-2х 1 х0,8х 1,1

Соответственно, а_у < 0. Следовательно, минимальная диспер­сия имеет место в случае, когда портфель состоит из одной бу­маги вида X. Средний доход от портфеля равен 2.

При полной отрицательной корреляции находим

1,1» - (-1)0,8 ж 1,1 _лс„

д — , ₌ Л k7Q

^х 0,8² - 1,1² - 2(-1)0,8 х 1,1 * * а_у= 1 -0,579 = 0,421.

Дисперсия в этом случае равна нулю (см. рис. 8.4), а средний доход составит 2,421.

179

Наконец, при отсутствии корреляции получим по формуле (8.12) а_х = 0,654; а_у = 1 - 0,654 = 0,346. Дисперсия дохода при такой структуре портфеля равна 0,418, а средний доход равен 2,346.

Пусть теперь портфель состоит из трех видов бумаг X, Y, Z. Их доли а_х, а_у и a_z = 1 - (а_х + а). Дисперсия дохода от порт­феля при условии независимости доходов от отдельных видов бумаг составит

D = a² DL + a² D + [1 - (а_х + a_v)]²D₇.

х х у У ^{1 х} У Z

Минимум дисперсии достигается, если структура портфеля определяется следующим образом:

А

У/1

^a* ⁼ -D~D.

'x/z "y/z ^{+ D}x/z ^{+ D}y/z

X/Z

^аУ D , D , + D , + D ,

x/z y/z x/z "y/z

He будем останавливаться на ситуации, когда доходы трех видов бумаг статистически зависимы. Перейдем к общей поста­новке задачи и определим структуру портфеля с л составляю­щими. Допустим, что доходы статистически независимы. Опус­тим доказательства¹ и приведем результат в матричном виде:

А = £Г'е,

(8.17)

где е — единичный вектор, характеризующий структуру порт­феля,

1

+ 1

D₂

+ 1

I 1

*»-!

4.-1

D„

180

Доказательства приведены в Математическом приложении к главе.

А -— вектор, характеризующий п — 1 элементов структуры порт­феля.

Матрица D имеет размерность (л — 1) х (л — 1).

ПРИМЕР 8.3. Эксперты оценили следующие отношения диспер­сий для портфеля, состоящего из четырех видов бумаг: D_1/4 = 1,5; D_2/4 = 2; D_3/4 =1. По формуле (8.17) получим

[2,5 1 11	-1	[0,210]
1 3 1	хв-	0,158
| 1 12		0,316

3 ^а4-¹-Ё^а/"¹-⁰'⁶⁸⁴"⁰'³¹⁶-

Заметим, что структуру портфеля, минимизирующую дис­персию дохода, с п составляющими при наличии корреляции определить так же просто, как это было сделано выше, нель­зя. Однако решение существует, хотя его получение достаточ­но хлопотное дело, да и вряд ли оно необходимо для практики.

Анализ диверсификации представляет собой первый этап в исследовании портфеля инвестиций. Следующим является ма­ксимизация дохода. Эта проблема также связана с измерением риска и требует обстоятельного специального обсуждения, вы­ходящего за рамки настоящего учебника. Поэтому ограничим­ся лишь замечанием о том, что метод Г. Марковица, который заключается в разработке и решении специальной модели не­линейного программирования с использованием показателей доходов и дисперсий, в теоретическом плане не вызывает воз­ражений. Что касается его практического применения, то здесь, на наш взгляд, скрыты серьезные подводные камни. За­тронем лишь одну проблему — какой срок для расчета диспер­сий следует принять во внимание? Если ограничиться неболь­шим сроком, то получим наиболее приближенные к современ­ности данные. Однако они могут оказаться неустойчивыми, со­держать много "шума", с другой стороны, стремление охватить максимальный срок неизбежно приведет к устареванию дан­ных.

181

Математическое приложение к главе

Минимум дисперсии дохода при отсутствии корреляции. Дисперсия в этом случае определяется выражением (8.2), ко-

торое для п долей запишем как

я-1

О)

Я- 2*,²4* 1-2*/ i \ \ I

В свою очередь

где

(■-'|*i) -l-22*;+(2*/)²,

/я-1 \² я-1 л-1 я-1

Окончательно имеем

2

/ /1-1 \ Я-1 Я-1 Я-1

Я-1

+ 2в_я-2^-1 ⁺ 2 */

(2)

Преобразуем (1) с использованием (2) и определим л - 1 ча­стных производных:

/'(*i)-*iA +

/я-1 \

/'(«₂)-^₂4|«/-ij^

(3)

182

/'(*«_,)-*„_,/>„_, + 1*/-1

D„.

Разделим каждое уравнение системы (3) на D_n и приравняем его нулю. После некоторых преобразований получим

«|ГБ- ⁺ Ч ⁺ «1 ^{+ в}э ⁺ " ⁺ «.-1-1.

«I +o₂\-^+\\ + a_i + ... + a^_l^l,

(4)

^а\ ^{+ а}2 ^{+ а}Ъ ⁺ —^{+ Д}л

+ i=i.

Представим систему уравнений (4) в матричном виде:

AD=e. После чего получим искомое уравнение (8.17):

А = Dr^xe.

ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА

1. Первозеанский А.А., Первозванская Т.Н. Финансовый рынок: Расчет и Риск. М.: Инфра-М, 1994. § 6.4.

2. Венецкий И.Г., Венецкая В.И. Основные математико-статистические понятия и формулы в экономическом анализе. М.: Финансы и статистика, 1979. С. 56-57.

3. Касимов Ю.Ф. Основы теории оптимального портфеля ценных бумаг. М.: Филинъ, 1998. Гл. 6, 7.