§3.4. Дисконтирование по сложной ставке

При изучении простых процентов мы рассматривали мате­матическое дисконтирование и банковский (коммерческий) учет. Первое заключалось в определении Р по значению S при заданной ставке процента, второе — при заданной учетной ставке. Применим первый метод и дисконтируем теперь сумму *Упо сложной ставке процентов. На основе (3.1) получим

P = -^T^T=Sv", (3.10)

_v- = (1 + ,уп = -L (з.ц)

Ч

Величину v называют дисконтным, учетным, или дисконти­рующим, множителем (compound discount factor). Значения этого множителя легко табулировать. В Приложении приведен фраг­мент такой таблицы (см. табл. 3).

Для случаев, когда проценты начисляются т раз в году, по­лучим

Р Sv^m\

_Л™ (3.12)

1 + ^-т

\*тп

-И+-£| • (3.13)

Напомним, что величину Р, полученную дисконтированием S, называют современной, текущей, стоимостью, или современ­ной величиной S. Современная стоимость может быть рассчита­на на любой момент до выплаты суммы S.

53

Разность S - Р, в случае, когда Р определено дисконтирова­нием, называют дисконтом. Обозначим последний через D:

Z) = 5- P= S(\ - V).

ПРИМЕР 3.10. Сумма в 5 млн руб. выплачивается через 5 лет. Необходимо определить ее современную величину при условии, что применяется ставка сложных процентов, равная 12% годовых. Дисконтный множитель для данных условий составит

у5₌1,12-5 = 0,56574,

т.е. первоначальная сумма сократилась почти на 44%. Совре­менная величина равна

Р = 5000 х 1,12-⁵ = 2837,1 тыс. руб.

Как уже отмечалось в гл. 2, современная величина платежа — одна из важнейших характеристик, применяемых в финансо­вом анализе. Кратко остановимся на некоторых ее формальных свойствах. Прежде всего отметим очевидное свойство — чем выше ставка процента, тем сильнее дисконтирование при всех прочих равных условиях (см. рис. 3.4). Например, если в при­мере 3.10 увеличить ставку вдвое, то дисконтный множитель снизится с 0,56574 до 0,34111.

Значение дисконтного множителя уменьшается и с ростом величины т.

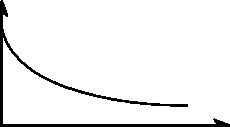
1

о ~ '

Рис. 3.4

Влияние срока платежа также очевидно — с увеличением срока величина современной стоимости убывает. Отсюда следу­ет, что при очень больших сроках она крайне незначительна. Например, если взять ставку / = 12% , то для п = 10, 50 и 100 находим следующие значения дисконтных множителей: 0,32197; 0,00346 и 0,000012.

54

Высокие, и особенно инфляционные, ставки, примененные для дисконтирования, приводят к бессмысленным результатам даже при сравнительно небольших сроках: например, для став­ки 200% и сроке 5 лет дисконтный множитель равен 0,004116, т.е. близок к нулю.

§3.5. Операции со сложной учетной ставкой

Учет по сложной учетной ставке. В практике учетных опера­ций иногда применяют сложную учетную ставку {compound dis-cound rate). В этих случаях процесс дисконтирования происхо­дит с замедлением, так как каждый раз учетная ставка приме­няется не к первоначальной сумме (как при простой учетной ставке), а к сумме, дисконтированной на предыдущем шаге во времени. Дисконтирование по сложной учетной ставке осуще­ствляется по формуле

Р =5(1 - d)\ (3.14)

где d — сложная годовая учетная ставка.

ПРИМЕР 3.11. Долговое обязательство на сумму 5 млн руб., срок оплаты которого наступает через 5 лет, продано с дискон­том по сложной учетной ставке 15% годовых. Каков размер полу­ченной за долг суммы и величина дисконта (в тыс. руб.)? Имеем

Р = 5000(1 - 0,15)⁵ = 2218,5; D = 5000 - 2218,5 = 2781,5.

Если применить простую учетную ставку того же размера, то

Р = 5000(1 - 5 х 0,15) = 1250; D = 5000 - 1250 = 3750.

Как следует из приведенного примера, дисконтирование по сложной учетной ставке выгоднее для должника, чем по про­стой учетной ставке. Сказанное становится понятным при срав­нении формул для дисконтных множителей:

w_s = (1 - nd_s) Hw=(l-rf)«,

где d_s, d — простая и сложная учетные ставки соответственно.

Согласно первой из приведенных формул значение дисконт­ного множителя равномерно уменьшается по мере роста п и до-

55

стигает нуля при п = \/d. Согласно второй — множитель экс­поненциально уменьшается и достигает нуля лишь в пределе, при п = оо. Величины дисконтных множителей при применении простой и сложной учетных ставок показаны на рис. 3.S

Рис. 3.5

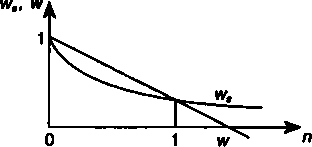
Номинальная и эффективная учетные ставки. Дисконтирова­ние может производиться не один, а т раз в году, т.е. каждый раз учет производится по ставке f/m . В этом случае

/>=£ 1

f\mn

т

(3.15)

где/— номинальная годовая учетная ставка.

Эффективная учетная ставка (d) характеризует степень дис­контирования за год. Определим ее на основе равенства дис­контных множителей:

откуда

f \mn (1-^ = |1-^|

d = 1

т

В свою очередь

/-m(l-*VT^f).

Эффективная учетная ставка во всех случаях, когда т > 1, меньше номинальной.

ПРИМЕР 3.12. По данным примера 3.11 определим сумму, полу­ченную при поквартальном учете по номинальной учетной ставке 15%, и эффективную учетную ставку. Имеемf = 0,15;т = 4;тп = 20;

56

^,(,-*5f-

P = 5000 1 - -^— = 2328,0 тыс. руб.

Эффективная учетная ставка составит

-^)'._w

( 0,15^4 d=1- 1--T— = 0.14177, или 14,177%.

Наращение по сложной учетной ставке. Иногда наращенную сумму получают и с помощью сложной учетной ставки. Из фор­мул (3.14) и (3.15) следует:

*-7П^г <^3|6>

т

Множитель наращения при использовании сложной ставки d равен (1 - d)~ⁿ.