
- •Оглавление
- •§1.2. Время как фактор в финансовых расчетах
- •§1.3. Проценты, виды процентных ставок
- •Глава 2
- •1. Точные проценты с точным числом дней ссуды (365/365):
- •2. Обыкновенные проценты с точным числом дней ссуды (360/365):
- •3. Обыкновенные проценты с приближенным числом дней ссу ды (360/360):
- •§ 2.2. Погашение задолженности частями
- •§2.3. Наращение процентов в потребительском кредите
- •§2.4. Дисконтирование по простым процентным ставкам. Наращение по учетной ставке
- •§2.5. Прямые и обратные задачи при начислении процентов и дисконтировании по простым ставкам
- •Дисконтные множители, I - d » 20%
- •§2.6. Определение срока ссуды и величины процентной ставки
- •§ 2.7. Конверсия валюты и наращение процентов
- •Глава 3 сложные проценты
- •§3.1. Начисление сложных годовых процентов
- •1 См.: Томас д. Воротилы финансового мира. М.: Прогресс, 1976.
- •§3.2. Сравнение роста по сложным и простым процентам
- •§3.3. Наращение процентов т раз в году. Номинальная и эффективная ставки
- •§3.4. Дисконтирование по сложной ставке
- •§3.5. Операции со сложной учетной ставкой
- •§3.6. Сравнение интенсивности процессов наращения
- •§3.7. Определение срока ссуды и размера процентной ставки
- •§3.8. Непрерывное наращение и дисконтирование. Непрерывные проценты
- •1 См. Математическое приложение к главе. 64
- •Глава 4
- •(IWf-lw/.NiwJt'...
- •§4.2. Эквивалентность процентных ставок
- •360 Х 0,4 лолло|г ллЛо«,п,
- •§4.3. Финансовая эквивалентность обязательств и конверсия платежей
- •§4.4. Общая постановка задачи изменения условий контракта
- •§4.5. Налоги и инфляция
- •1 Доказательство (4.38) см. В Математическом приложении к главе. 82
- •1 См. Математическое приложение к главе.
- •§4.6. Кривые доходности
- •1 В гл. 7 приводится пример выбора поведения инвестора в зависимости от ожиданий размера процентной ставки.
- •1. Приведем доказательство формулы (4.38). По определению
- •2. Докажем формулу (4.41):
- •Глава 5
- •§5.1. Виды потоков платежей и их основные параметры
- •1 В переводной литературе обычно не различают термины: поток платежей и член потока.
- •1 Июля 1 января 2000 г. 2001 г.
- •1 Января 1 января 2003 г. 2004 г.
- •§5.2. Наращенная сумма постоянной ренты постнумерандо
- •§5.3. Современная стоимость постоянной ренты постнумерандо
- •§5.4. Определение параметров постоянных рент постнумерандо
- •§5.5. Наращенные суммы и современные стоимости других видов постоянных рент
- •1 |П 1,2 ' oiUMct.
- •Глава 6
- •1 Доказательство приведено в Математическом приложении к главе. 126
- •§6.2. Ренты с постоянным относительным приростом платежей
- •§6.3. Постоянная непрерывная рента
- •§6.4. Непрерывные переменные потоки платежей
- •1 Доказательство см. В Математическом приложении к главе.
- •§6.5. Конверсии рент
- •§6.6. Изменение параметров рент
- •Глава 7
- •§7.2. Нелинейные модели
- •§7.3. Барьерные показатели в финансовом анализе
- •§7.4. Влияние неопределенности в исходных данных на положение барьерной точки
- •§7.5. Барьерные точки выпуска — финансовый подход к их определению
- •Глава 8 риск и диверсификация
- •§8.1 Риск
- •§8.2. Диверсификация инвестиций и дисперсия дохода
- •1 Напомним следующие свойства коэффициента корреляции:
- •1 В странах со стабильной экономикой безрисковой обычно считается ценная бумага, выпущенная государственным казначейством.
- •§8.3. Минимизация дисперсии дохода
- •Глава 9
- •§9.1. Расходы по обслуживанию долга
- •§9.2. Создание погасительного фонда
- •22%. Необходимо найти размеры срочных уплат. Пусть фонд формируется 5 лет, взносы производятся в конце каждого года равными суммами.
- •§9.3. Погашение долга в рассрочку
- •§9.4. Льготные займы и кредиты
- •§9.5. Реструктурирование займа
- •§9.6. Ипотечные ссуды
- •§9.7. Расчеты по ипотечным ссудам
- •Глава 10 измерение доходности
- •§10.1. Полная доходность
- •§10.2. Уравнение эквивалентности
- •§10.3. Доходность ссудных и учетных операций с удержанием комиссионных
- •§10.4. Доходность купли-продажи финансовых инструментов
- •§10.5. Долгосрочные ссуды
- •§10.6. Упрощенные методы измерения доходности (долгосрочные ссуды)
- •Дополнительная литература
- •Глава 11 облигации
- •§11.1. Виды облигаций и их рейтинг
- •§11.2. Измерение доходности облигаций
- •§11.3. Дополнительные сведения по измерению доходности облигаций
- •§11.4. Характеристики сроков поступлений средств и измерение риска
- •§11.5. Оценивание займов и облигаций
- •Глава 12
- •§12.2. Чистый приведенный доход
- •§12.3. Свойства чистого приведенного дохода
- •§12.4. Внутренняя норма доходности
- •1 В сопровождающем программу тексте этот показатель ошибочно назван "скоростью оборота".
- •2 Для определения внутренней нормы доходности применяется итерацион ный процесс, поэтому желательно указать некоторое ориентировочное началь ное значение ставки.
- •§12.5. Срок окупаемости
- •§12.6. Индекс доходности
- •§12.7. Соотношения относительных измерителей эффективности
- •§12.8. Сравнение результатов оценки эффективности
- •§12.9. Моделирование инвестиционного процесса
- •§12.10. Анализ отзывчивости
- •Математическое приложение к главе
- •Глава 13 лизинг
- •§13Л. Финансовый и оперативный лизинг
- •§13.2. Схемы погашения задолженности по лизинговому контракту
- •Периодические платежи по лизингу
- •§13.3. Методы расчета лизинговых платежей
- •1. Платежи постнумерандо
- •2. Платежи пренумерандо
- •Глава 14 форфейтная операция
- •§14.1. Сущность операции а форфэ
- •§14.2. Анализ позиции продавца
- •§14.3. Анализ позиций покупателя и банка
- •Глава 15 коротко об опционах
- •§15.1. Сущность опциона, основные понятия
- •§15.2. Цена опциона
- •§15.3. Модель Блека—Шоулза
- •Глава 16 страховые аннуитеты
- •§16.1. Финансовая эквивалентность в страховании
- •§16.2. Таблицы смертности и страховые вероятности
- •1 Во всех примерах данного параграфа используется таблица смертности населения ссср 1984—1985 гг.
- •§16.3. Коммутационные функции
- •Фрагмент таблицы коммутационных чисел1
- •§16.4. Стоимость страхового аннуитета
- •20|Лзо:51 Озо уЗю.З V.Oowo.
- •Глава 17 личное страхование
- •§17.1. Нетто-премии в личном страховании
- •1 Значения коммутационных чисел, приведенные в примерах, взяты из табл. 12 Приложения.
- •§17.2. Страхование жизни
- •§17.3. Пенсионное страхование. Виды пенсионных схем
- •§17.4. Расчет премий и пенсий. Сберегательные схемы
- •40 60 75 " Возраст
- •§17.5. Страховые пенсионные схемы
- •Расчет размера пенсии
- •§17.6. Страховые резервы в личном страховании
- •82 461 1 Ю iPso '
- •Коммерческий отдел — тел. 433-2510, 433-2502
- •Internet: http://www.Deio.Ane.Ru
- •Isbn 5-77494)193-9
§7.2. Нелинейные модели
Линейная модель во многих случаях дает практически приемлемое описание ситуации. Однако могут иметь место ситуации, когда процесс формирования затрат и/или стоимости продукции более адекватно описывается нелинейными функциями и имеются достаточно надежные данные для получения соответствующих кривых. Вид и параметры таких кривых могут быть установлены, например, в ходе статистического анализа или их можно задать экспертно.
Барьерный выпуск продукции. Вернемся к задаче по определению критического объема продукции, но в условиях, когда одна или обе "конкурирующих" функции являются нелинейными. Ограничимся двумя из возможных постановок задачи. Пусть для начала стоимость продукции — линейная функция выпуска, а затраты на производство описываются нелинейной, монотонно растущей функцией. Иначе говоря, предполагается, что удельные затраты сокращаются по мере роста масштабов производства, а цена единицы продукции не изменяется. Такое сочетание затрат и стоимости продукции представлено на рис. 7.3.
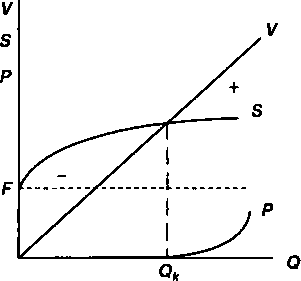
Рис, 7,3
Задача, как и выше, заключается в определении барьерного уровня выпуска продукции. Стоимость продукции находится по формуле (7.1), а сумма переменных затрат описывается, допустим, степенной функцией cQh, причем 0 < А < 1. В этом случае общая сумма затрат составит
153
5= F+ cQh
Разность "конкурирующих" функций в барьерной точке равна нулю:
pQk~cQ\- F=0.
Решение, как видим, сводится к нахождению корня этого уравнения.
|
ПРИМЕР 7.2. Исходные данные: F Соответственно имеем |
= 100, p = |
50, с = 40, h |
= 0,5. | ||
|
|
50Qk - 40Q°'5 - |
- 100 |
= 0. |
|
|
|
Найдем корни этого уравнения. квадратное, положив О = z2. После |
Для чего |
этого преобразуем получим |
его в | ||
|
*«-■ |
50z2 - 40z - |
100 = |
= 0, |
|
|
|
-(-40)±^40)2 27 |
-4х! 50 |
50 х(- |
-юо) | ||
|
Положительный = 1,862 = 3,46. |
корень равен |
1,86. |
Таким образом, |
°*= | |
Перейдем к сочетанию двух нелинейных зависимостей. Например, пусть обе функции являются параболами второй степени (см. рис. 7.4). Тогда
V= aQ2 + bQ, S=cQ2 + dQ +F,
где a, b, c, d — параметры парабол.
Прибыль в зависимости от уровня выпуска составит
Р = {а - c)Q2 + {b-d)Q- F (7.5)
Барьерный объем выпуска находится как корень квадратного уравнения
(a-c)Q2k + (b-d)Qk-F=0. 154
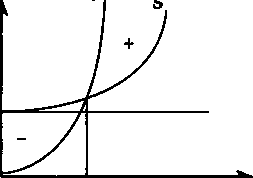
F
 Ok 0
Ok 0
Рис. 7.4
Добавим, что при некоторых условиях можно рассчитать объем выпуска, максимизирующего размер прибыли (обозначим его как Qm). Для этого, как известно, достаточно найти производную функции прибыли и приравнять ее нулю. В случае, когда прибыль описывается выражением (7.S), находим
g»-t^t- <7-6>
Как видим, положение точки максимума полностью определяется параметрами соответствующих парабол. Причем необходимым условием существования максимума являются следующие соотношения: d>b, a>c . Если же b>d и а>с, то прибыль монотонно растет вместе с увеличением выпуска.
Нелинейную модель можно представить и в неформализованном виде — как таблицу данных, характеризующих затраты и стоимость продукции в зависимости от размера выпуска (см. пример 7.3).
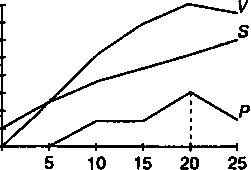
ПРИМЕР 7.3. В приведенной ниже таблице и на диаграмме содержатся данные о затратах, стоимости продукции и ожидаемой прибыли.
|
о |
F |
с |
Р |
S |
V |
Р |
|
0 |
100 |
— |
— |
100 |
— |
— |
|
5 |
100 |
30 |
50 |
250 |
250 |
0 |
|
10 |
100 |
27 |
50 |
370 |
500 |
130 |
|
15 |
100 |
22 |
45 |
430 |
675 |
145 |
|
20 |
100 |
20 |
40 |
500 |
800 |
300 |
|
25 |
100 |
20 |
30 |
600 |
750 |
150 |
155
 V,
S, P
V,
S, P
800
700-
600-
500-
400
300-
200
100-
0
Рис, 7,5
Наибольшая прибыль, как видим, приходится на выпуск, равный 20.
