§5.3. Современная стоимость постоянной ренты постнумерандо

Годовая рента. Напомним, что под современной стоимостью потока платежей понимают сумму дисконтированных членов этого потока на некоторый предшествующий момент времени. Вместо термина "современная стоимость" (современная вели­чина) потока платежей в зависимости от контекста употребля­ют термины капитализированная стоимость или приведенная ее-личина. Как было показано выше, современная стоимость пото­ка платежей эквивалентна в финансовом смысле всем плате­жам, которые охватывает поток. В связи с этим данный показа­тель находит широкое применение в разнообразных финансо­вых расчетах (планирование погашения долгосрочных займов, реструктурирование долга, оценка и сравнение эффективности производственных инвестиций и т.д.). В общем виде метод оп­ределения современной величины потока платежей (метод пря­мого счета) рассмотрен в § 5.1. Здесь же объектом анализа яв­ляется постоянная финансовая рента постнумерандо.

Методы расчета современных стоимостей финансовых рент обсудим в том же порядке, что и методы наращения рент и поч­ти столь же детально. Начнем с самого простого случая — го­довой ренты постнумерандо, член которой равен R, срок ренты — п, ежегодное дисконтирование. Рента немедленная. В этих условиях дисконтированная величина первого платежа равна Rv, второго — Rv², последнего — Rv". Как видим, эти величи­ны образуют ряд, соответствующий геометрической профессии с первым членом Rv и знаменателем v. Обозначим сумму чле­нов этой профессии через А:

A-Ryv' = Rv- --R—^V--

h v-i

/ х- (5-14)

1- (l + i)

I

Назовем множитель, на который умножается R, коэффициен­том приведения ренты, он обозначен как а_пЧ (в литературе встречается обозначение a_n,j). Этот коэффициент характеризует современную стоимость ренты с членом, равным 1. Значения a_n;i табулированы (см. табл. 7 Приложения).

107

Поскольку рассматриваемый параметр часто применяется в финансовых расчетах, полезно, обратить внимание на некоторые его свойства. Очевидно, что чем выше значение /', тем меньше величина коэффициента. Нетрудно показать, что при / = О

%=о ^{= Л}-

При увеличении срока ренты величина а_пЛ стремится к не­которому пределу. При п = » предельное значение коэффици­ента составит

lim

!-(!♦«)-

(5.15)

Полученное выражение применяется при расчете современ­ной стоимости вечной ренты, о чем пойдет речь в § 5.5.

График зависимости а_пЧ от п показан на рис. 5.2.

Воспользуемся формулой (5.14) для определения взаимосвя­зи коэффициентов приведения ограниченной и вечной рент:

"„;/ =

1

(1 + /Г" 1 1

_{. =7 " °} ⁺ _°~"^х _у ⁼ _{° "} ^уМ)а_~*^т

В последней записи искомый коэффициент приведения оп­ределен как доля коэффициента приведения вечной ренты, за­висящая от срока ренты.

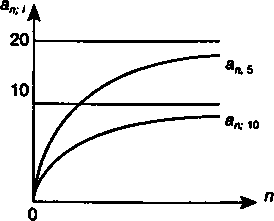
Рис. 5.2

ПРИМЕР 5.9. Годовая рента постнумерандо характеризуется па­раметрами: Я = 4 млн руб, п = 5. При дисконтировании по слож­ной ставке процента, равной 18,5 % годовых, получим

108

1 - 1.185"^{5 А} =4a*iRs =^4хГТ^ =^4х3,092 = 12,368 млн руб.

5,18,5 о,185

Таким образом, все будущие платежи оцениваются в настоя­щий момент в сумме 12,368 млн руб. Иначе говоря, 12,368 млн руб., размещенных под 18,5% годовых, обеспечивают ежегодную выплату по 4 млн руб. в течение 5 лет.

Заметим, что формула (5.14) может быть применена и для определения современной стоимости /ьсрочной ренты. В этом случае переменная п означает число периодов ренты, а / — став­ку за один период (но не годовую).

Коэффициент приведения ренты за срок п = л, + п₂ опреде­ляется следующим образом:

^ан;1 - Я*,;/

+ в|.₂У¹- (5.16)

Годовая рента, начисление процентов т раз в году. Не будем выводить формулу для этого случая, а просто заменим в форму­ле (5.14) дисконтный множитель (1 + /)~^/| на эквивалентную ве­личину (1 + j/m)~^mn, соответственно, / заменим на (1 + j/m)^m -— 1, после чего имеем:

1 -(1 +7/тГ'™

Л = R _/л , .. _чт — = Ra_mn._i/m. (5.17)

(1 +у//и)^т - 1 ^mnj/m

Рента /^-срочная (т = 1). Если платежи производятся не один, а р раз в году, то коэффициенты приведения находятся так же, как это было сделано для годовой ренты. Только теперь размер платежа равен R/p, а число членов составит пр. Сумма дисконтированных платежей в этом случае равна

А - - ? v^t/p - R _r¹"'^1+l' - Ra^{p). (5.18)

ПРИМЕР 5.10. В первой главе упоминалась авария на химиче­ском заводе в Бхопале (Индия). Корпорация "Юнион Карбайд" предложила в качестве компенсации пострадавшим 200 млн долл., выплачиваемых в течение 35 лет. Предложение было от­клонено ("За рубежом". 1985. № 11). Предложенная компенсация

109

эквивалентна 57,5 млн долл., выплаченных единовременно. Пока­жем, как была рассчитана эта сумма.

Если выплаты производятся помесячно на протяжении 35 лет равными суммами, то данный ряд платежей представляет собой постоянную ренту (р = 12) с годовой суммой выплат 200/35 = = 5,714 млн долл. в год. Допустим, это рента постнумерандо. То­гда согласно (5.18), положив / = 10% , получим

1 - 1,1-35 А = 5,714 _{1 11/12} _ = 57,59 млн долл.

Иначе говоря, капитал в сумме всего 57,59 млн долл. при на­числении 10% годовых достаточен для выполнения обязательства.

Рента ^-срочная (р = /и). Число членов ренты здесь равно числу начислений процентов; величина члена ренты составляет R/m . В итоге

R 1 -(1 +7/w)-"^w 1 -(1 +у/тГ™

А = х = R : . (5.19)

т j/m j

Этот же результат можно получить и по формуле (5.14) и при этом воспользоваться таблицей коэффициентов приведения по­стоянных рент. В этом случае вместо числа лет берется количе­ство периодов ренты, процентная ставка и величина члена рен­ты определяются соответствующим образом.

Для расчета современной стоимости платежей ренты с усло­вием р = т можно воспользоваться программой ПЗ (PV) паке­та Excel, которая определяет величину А с учетом единовремен­ного взноса в конце срока. Расчет производится по формуле

А = R х a_n;i + БС х (1 + /Г^Л,

где R — член ренты, БС — единовременный взнос, a_n;i — коэф­фициент приведения постоянной ренты, п — число'периодов выплаты ренты и начисления процентов, / — процентная став­ка за период.

Последовательность действий при использовании программы ПЗ

1. Последовательно вызвать: £, "финансовые функции", ПЗ.

2. Показать в строках окошка условия выплаты ренты, размер единовременного платежа и порядок начисления процентов:

по

Норма — ставка начисляемых процентов за период, Клер — число периодов,

Выплата — член ренты; показывается с отрицательным знаком,

БС — единовременный взнос в конце срока, показывает­ся с отрицательным знаком. Если эта величина не указы­вается, то результат — современная стоимость постоянной ренты,

Тип — вид ренты, указать 0 для ренты постнумерандо и 1 — для ренты пренумерандо. Если вид ренты не указывает­ся, то расчет ведется для ренты постнумерандо.

После выполнения действий 1—2 в итоговой строке Значе­ние автоматически показывается расчетная величина. После на­жатия кнопки ОК эта величина показывается в выделенной ячейке таблицы Excel.

ПРИМЕР 5.11. Параметры ренты пренумерандо: R = 100 (годо­вая выплата), п = 5, р = т = 2. Общее число платежей — 10, ставка за полугодие 6%. Введем параметры в окошко програм­мы ПЗ:

Норма: 6%, Кпер: 10, Выплата: -50, Тип: 1, Ответ: 390,085.

Рента /ьсрочная (р * т). Сумма членов соответствующей прогрессии составит

Л ⁼ а _г/, , .. _Чт/я — - &^а .и • (5.20)

Ренты с непрерывным начислением процентов. Пусть, как и выше, ряд состоит из ежегодных платежей, равных Л, однако проценты начисляются непрерывно, сила роста равна 6. При дисконтировании по этой ставке всех членов ряда получим геометрическую прогрессию с первым членом R и знаменате­лем ё~^ь. Сумма членов прогрессии находится следующим об­разом:

1 - е"^6я A-R-j—^-Ra^. (5.21)

ill

Если имеет место р-срочная рента с непрерывным начисле­нием процентов, то

1 — е~^Ьп А = R—TJTn—77 = Л!^ (5.22)

ПРИМЕР 5.12. Для условий примера 5.9 при 6 = 0,185 находим

1 _ _е-0,185х5 ^{А = 4} о,185 - ^{= 11} »^{878 МЛН Р}У^б>

Сравнение современных стоимостей рент постнумерандо с раз­ными условиями. Как следует из приведенных примеров, вели­чина современной стоимости заметно зависит от условий нара­щения процентов (точнее, дисконтирования) и частоты выплат в пределах года. Ниже приводятся соотношения современных стоимостей соответствующих рент. Современные стоимости обозначены как А(р;т), причем запись А(\;1) означает годовую ренту с ежегодным начислением процентов, А(р; ») относится к /ьсрочной ренте с непрерывным начислением процентов.

Для одних и тех же годовых сумм выплат и процентных ста­вок (/ =у =6) получим следующие неравенства:

А( 1;») < А( 1 ;/и) < Л( 1; 1) < А(р;*>) < А{р\т) < А{р\т) < А(р\т) < А(р; 1).

т>р>\ р=т>1 р>т>\

Из приведенных неравенств, в частности, следует, что рента с условиями р = 4 и т = 2 имеет меньшую современную стои­мость, чем рента с/; = 2и/и = 4.

Зависимость между наращенной и современной стоимостью ренты. В § 5.2 была показана зависимость между А и S произ­вольного потока платежей (см (5.3)). Для годовых и р-срочных постоянных рент постнумерандо с ежегодным начислением процентов находим

1 - (1 + /Г" (1 + 0^я - 1 А(\ + /)^л = R ———0 + 0^я = Я¹ : = S. (5.23)

Аналогичным образом получим

Svⁿ = A.

112

Для рент с начислением процентов т раз в году имеем

А{\ +j/m)^mn = 5, (5.24)

S(l +j/my^mn = A. (5.25)

Нетрудно догадаться, что в аналогичной зависимости нахо­дятся и коэффициенты наращения и приведения. В частности,

a_n;i(\ + 0- = 5_Л;/, s_n;iv» = а_п._г

ПРИМЕР 5.13. Найдем современную стоимость для варианта ренты р = т = 4, взяв за основу S = 31,785 (см. пример 5.6). По формуле (5.24) получим

/ 0,185 V²⁰ А = 31,785 1 +—_А— = 12,868 млн руб.