2.8.3 Нелінійні перетворення випадкових сигналів

Якщо при розгляданнi проходження випадкового сигналу повз лiнiйну ланку застосувалися методи усереднення за часом (кореляцiйнi функцiї та спектральнi щільності), то для нелiнiйних ланок основою дослiдження є метод усереднення за множиною (закони розподiлу).

Розглянемо безiнерцiйну нелiнiйну ланку з монотонно зростаючою характеристикою (Рис.2.184) , на вхiд якої поступає випадковий сигнал , де - математичне очікування, - центрована випадкова складова, у виглядi ансамблю реалiзацiй, який характеризується у момент , щільністю розподiлу .

Рис. 2.2134 Проходження випадкового сигналу через нелінійну ланку

Коли рiвень завад малий та не виходить за межи лiнiйних дiлянок нелiнiйностi з сталими значеннями похiдних, вихiдний сигнал можна визначити як

Але з пiдвищенням рiвня завад, коли вхiдний сигнал виходить за межи лiнiйних дiлянок, середнє значення вихiдного сигналу буде зменшуватися та одночасно змiнюється спектральний склад вихiдного випадкового процесу. При цьому щільність розподiлу сигналу може бути знайдено з умови рiвностi iмовiрностей сигналу на входi до деякої областi та сигналу на виходi до областi , де . Тодi , та .

Цей вираз дає можливiсть по вiдомим характеристикам та знайти залежнiсть . Але коли нелiнiйна характеристика неоднозначна, то визначення щільності розподiлу сигналу на виходi нелiнiйностi значно ускладнюється, тому що щільність розподiлу буде вже залежить не тiльки вiд щільності розподiлу сигналу на входi, але i вiд імовірнісних характеристик його похiдної за часом.

Отже, для випадкового сигналу треба знати щільність розподiлу самого сигналу, його похiдної та двомірну щільність розподiлу . Якщо вiдомо математичне очікування (момент першого порядку) на входi нелiнiйної ланки та на виходi то таким чином можна визначити перетворення моментiв першого порядку нелiнiйною ланкою.

Так для сигналу з нормальним розподiлом закон перетворення моменту першого порядку буде залежати не тільки вiд виду та 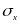, але i вiд

Рис. 2.215 Перетворення статистичних характеристик нелінійною ланкою

Момент другого порядку на виходi та входi нелiнiйної ланки визначається таким чином

Дисперсія сигналiв на виходi та входi визначається через моменти першого та другого порядкiв

За нормальним розподiлом вхiдного сигналу закон перетворення моменту другого порядку залежить вiд та

2.8.4 Статистична лінеаризація нелiнiйної ланки

Метод статистичної лінеаризації засновано на замiнi нелiнiйних перетворень випадкових процесiв статистично еквiвалентними їм лiнiйними перетвореннями. При цьому нелiнiйна ланка, на вхід якої дiє процес , замiнюється лiнiйним еквiвалентом.

Цей метод засновано на двох критерiях статистичної еквiвалентностi.

Перший з них потребує рiвностi математичних очікувань та дисперсiй сигналiв на виходi нелiнiйної та лiнiйної ланок (Рис.2.216).

Рис. 2.216 До задачі статистичної лінеаризації

Другий критерiй потребує мiнiмiзацiї середнього квадрату рiзницi процесiв на виходах цих ланок.

Хай процеси на входi та виходi нелiнiйної ланки мають вигляд

Виконаємо статистичну лінеаризацію нелiнiйної ланки з урахуванням вiдповiдних критерiїв

де - коефiцiєнт передачі по математичному очікуванню;

- коефiцiєнт передачі по центрованої складової.

З умови першого критерiю повинні виконуватися спiввiдношення

(2.298)

Значенню та , при яких задовольняється перший критерiй еквiвалентностi для однозначних нелiнiйностей визначаються за формулами

Із другого критерію еквiвалентностi маємо

(2.299)

або

За умови та

Знаходимо

Якщо закон розподiлу сигналу на входi нормальний

то та залежать тiльки вiд двох параметрiв - математичного очікування та дисперсiї , тобто

Рис. 2.217 Статистична лінеаризація нелінійності

Розглянемо нелiнiйну систему (Рис.2.218) на вхiд якої поступає детермiнований корисний сигнал та центрована стацiонарна завада , статичнi характеристики якої вiдомi ( ).

Рис. 2.218 Структурна схема нелінійної системи

Пiсля виконання статистичної лінеаризації нелiнiйностi структурна схема приймає вигляд (Рис.2.219)

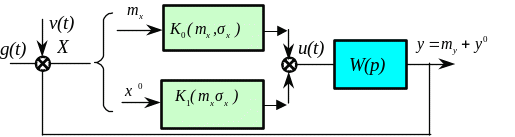
Рис. 2.219 Еквівалентна схема системи з статистичною лінеаризацією

По першому каналу проходить повiльна складова , а по другому - швидка випадкова складова . Будемо вважати, що до лiнiйної частини виконується гiпотеза фiльтру: на виходi лiнiйної частини сигнал має нормальний закон розподiлу незалежно вiд закону розподiлу сигналу на входi. Тодi сигнал представляє собою рiзницю сигналiв, якi задовольняють нормальному закону, і, отже, також має нормальний закон розподiлу.

Визначимо стале значення сигналу похибки при по першому каналу

Для другого каналу дисперсiя сигналу х визначається по спектральнiй щільності

Таким чином, здобуваємо два рівняння ,

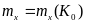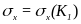
Тому що в цих рівняннях є чотири невiдомих величини то необхiднi два рiвняння здобуваються iз умови проходження сигналу х повз нелiнiйну ланку

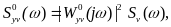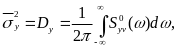Отже, розв`язуючи цю систему рiвнянь, здобуваємо значення та , якi вiдображають імовірнісні характеристики разузгодження у слiдкуючої системi. Тому що завада не перекручує сталої складової, то знайдена величина вiдображає сталу похибку системи при дiї завади . Випадкова складова похибки визначається по спектральної щільності складової сигналу на виходi, яка обумовлена завадою де . Тодi що дозволяє знайти загальну середньоквадратичну похибку системи .

Так для випадку ,

маємо

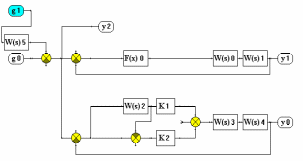
Рис.2.220 Моделювання нелінійної системи із статистичною лінеаризацією

Рис. 2.221 Процеси в задачі моделювання статистичної лінеаризації