Дійсно, хай дискретне рівняння має вигляд

Якщо використати підстановку ,то

,

і після групування коефіцієнтів при однакових степенях одержимо

, (2.137)

де

Так, при

Використовуючи заміну ,здобудемо

Використовуючи рівняння відносно оператору зсуву можна здобути рішення через рекурентне співвідношення

(2.138)

яке дозволяє визначити послідовність ,..., якщо визначені початкові умови та значенням дискретної функції Алгоритм рішення легко реалізується на ЕОМ.

Хай задано дискретне рівняння та визначені i .

Отже,

Рис .2.80

У загальному випадку рішення дискретного рівняння складається з вільного та вимушеного руху

, (2.139)

де визначає вільний рух, як рішення однорідного рівняння

(2.140)

а визначає вимушений рух, як окреме рішення, яке залежить від виду вхідного сигналу.

Вільне рішення здобувається у вигляді (2.141)

де - корені характеристичного рівняння

Аналіз вільного руху показує, що для стійкого руху необхідно і достатньо, щоб використовувались умови , (2.141), тобто, властиві значення характеристичного поліному стійкого руху повинні належати колу одиничного радіусу (Рис.2.81).

Рис .2.81

Очевидно, що коли дійсні, то представляє собою монотонний процес, коли - комплексні, то процес буде коливальним, якщо , то процес буде встановлюватись за один крок.

2.5.2 Складання дискретних рівнянь лінійних систем

Методику складання дискретних рівнянь розглянемо відносно умови функціонування дискретних систем автоматичного управління. Замкнення системи виконується тільки у моменти роботи ідеального імпульсного моменту, тобто у моменти квантування , а у проміжках між моментами квантування система працює як розімкнена при сталому впливі - сигналі, який зберігається на виході формуючої частини імпульсного елементу.

Хай у дискретній системі імпульсний елемент генерує послідовності імпульсів прямокутної форми з періодом та тривалістю , а лінійна частина описується оператором (Рис.2.82).

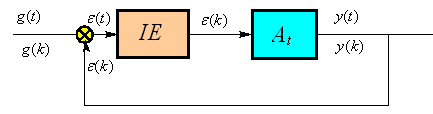
Рис.2.82

Вихідний процес , який протікає усередині будь-якого інтервалу дискретності

має вигляд

(2.142)

де _.

Кінцеве значення на -тому інтервалі, а отже і початкове значення на інтервалі приймає вигляд

Якщо неперервна частина дискретної системи має -тий порядок, то для визначення рішення необхідно розглядати процес у n попередніх інтервалах дискретності, що зведе рішення до вигляду

(2.143)

Хай лінійна частина дискретної системи має передаточну функцію ,

а імпульсний елемент генерує послідовність імпульсів прямокутної форми з періодом та скважністю . Визначимо рішення диференційного рівняння системи у межах одного циклу квантування , який складається із двох рішень на інтервалах та , тобто як рішення рівнянь та .

Рішення на першому інтервалі буде

Постійна інтегрування отримується з урахуванням початкових умов для моменту _.

,

Отже, _.

На другому інтервалі

Тому що значення на початку інтервалу, тобто при дорівнює значенню на кінці першого інтервалу, то

Отже,

При одержуємо

З умови замкнення системи маємо а якщо система замикається одиничним зворотнім зв'язком, то

Отже,

що після перетворень дає

Якщо , то

Тому що , то при , , a _.Із характеристичне рівняння приймає вигляд .Отже,

При , тобто . Таким чином

Хай , тоді .

Якщо , то процес встановлюється за один крок, система стійка і має найменший час перехідного процесу .

1) При, , що дає коливальний перехідний процес.

2) При процес буде монотонним.

3) При система на межі стійкості.

4) При система стає нестійкою.

Рис. 2.83 Вплив кореня на вигляд перехідних процесів