2.4.4 Поняття змінних стану та фазового простору.

При складанні рівнянь динаміки нелінійної системи всі ланки, які підлягають лінеаризації у межах малих відхилень координат у робочих точках, описуються лінійними рівняннями. Для нелінійних ланок складаються нелінійні рівняння.

Отже, у загальному випадку система буде описуватися нелінійними диференційними рівняннями динаміки, які можуть бути представлені у нормальному вигляді

(2.109)

де - координати стану системи,

- відповідно задаючі та збуджуючі впливи,

- нелінійні функції, які задовольняють при визначених початкових значеннях умовам існування рішення .

При відсутності зовнішніх впливів для розглядання перехідних процесів, які викликаються деякими відхиленнями початковими координат, ці рівняння для систем з постійними параметрами приймають вигляд

У просторі стану значення функцій будуть представляти координати деякої точки, яка називається зображуючою точкою.

При зміні часу (розглядається як параметр) ця точка описує у фазовому просторі деяку криву , яка називається фазовою траєкторією.

Положенню рівноваги системи відповідають особливі точки, а замкненим траєкторіям - особливі лінії, які називають граничними циклами.

2.4.5 Опис систем керування на фазової площині.

Для багатомірних систем фазовий простір є погано обозримим, що ускладнює геометричну інтерпретацію цього методу дослідження.

Якщо ж система описується диференційними рівняннями другого порядку, то фазовий простір перетворюється у фазову площину.

Фазовою площиною називається площина, у якої по осям координат відкладаються які-небудь дві змінні, які характеризують перехідний процес у системі.

Найбільш часто в якості таких змінних приймають відхилення регульованої величини та швидкість її зміни.

При зображенні процесів на фазовій площині рівняння динаміки системи другого порядку приводяться до системи рівнянь першого порядку, тобто представляються у вигляді

(2.110)

Щоб зобразити перехідний процес у фазовій площині із рівнянь треба виключити незалежну змінну .

Тоді диференційне рівняння фазової траєкторії приймають вигляд

(2.111)

і, отже, , рішення якого дає на фазовій площині фазову траєкторію. Параметр визначає постійну інтегрування, яка залежить від початкових умов .

Отже, кожній сукупності початкових умов буде відповідати своя фазова траєкторія.

Якщо ж функції є однозначними, то кожній точці фазової площини відповідає тільки одне значення похідної

(2.112)

А це означає, що через кожну точку на фазовій площині проходить тільки одна фазова траєкторія, відкіля слідує висновок про те, що фазові траєкторії однієї системи не перехрещуються.

Якщо на фазовій площині визначити геометричне місце точки, у якої похідна то на площині зобразяться деякі лінії, які називаються ізоклінами.

Тому що чисельне значення похідної дорівнює кутовому коефіцієнту дотичних, то за умовами постійності похідної можна визначити кутовий коефіцієнт траєкторії .

Отже, якщо задаватися деякими сталими значеннями кутового коефіцієнта , то можна знайти сім'ю ізоклін на фазовій площині.

У свою чергу, якщо задати значення кутового коефіцієнту , то можна визначити: кутовий коефіцієнт самої ізокліни

(2.113)

Внаслідок того, що при своєму руху зображуюча точка повинна перетинати ізокліну під цілком визначеним кутом, то вона буде послідовно перетинати ізокліни і описувати на фазовій площині фазову траєкторію.

Очевидно, що точки, які відповідають врівноваженим станам системи

є особливими точками.

Якщо у процесі руху зображаюча точка буде наближатися до особливих точок врівноваженого стану, то рух у системі буде стійким.

Якщо ж зображаюча точка буде віддалятися від таких особливих точок, то це буде свідчити про нестійкість системи.

Рис.2.52 Фазовий портрет нелінійної системи

У випадку, якщо фазові траєкторії у деяких областях фазового простору стають замкненими, то це буде свідчити про появу у системі граничних циклів, що відповідає появі у системі періодичних коливань із сталими параметрами, амплітудою та частотою.

Якщо разові траєкторії підходять до ліній граничного циклу із зовнішнього та внутрішнього боків, то у системі існує особливий вид руху, стійкий граничний цикл, тобто режим автоколивань, які характеризуються своїми значеннями амплітуди та частоти.

Розглянемо динаміку процесів у нелінійній системі (Рис.2.53), рівняння якої мають вигляд

Рис.2.53 Замкнута нелінійна система 2-го порядку

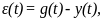
де ; .

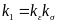На основі системи рівнянь знайдемо рівняння відносно входу нелінійного елементу

Хай нелінійний елемент - релейний підсилювач із зоною нечутливості (Рис.2.54).

Визначимо властивий рух у системі, коли , а початкові умови визначаються початковим відхиленням .

Рис.2.54 Характеристика не лінійності із зоною нечутливості

Отже, при на основі (Рис.2.53) буде виконуватися , що при обумовлює вихід нелінійного елементу .

При , якщо будуть виконуватись умови , ,

А при .

Таким чином, у залежності від значення похибки , а, отже, від значення сигналу на вході нелінійного елементу, динаміка системи буде визначатися такими співвідношеннями

(2.114)

Дослідження будемо виконувати відносно похибки системи, яку можна спостерігати у системі.

Отже, з урахуванням, що рівняння приймають вигляд

Якщо за фазові змінні прийняти похибку та її швидкість то рівняння фазових змінних визначається у вигляді системи диференційних рівнянь першого порядку (при )

Виключивши незалежну змінну із системи рівнянь, здобудемо

або , розв’язок якого має вигляд

та визначає траєкторію руху зображаючої точки на першому етапі.

Якщо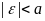 , то рух на другому етапі визначається рівняннями

або

Відповідно на третьому етапі рівняння приймають вигляд

Хай система стартує з початкової точки, яка визначається координатами

Рис.2.55 Рух відображаючої точки на фазової площині

Побудова фазових траєкторій ведеться доти, доки відображаюча точка не потрапить у зону нечутливості нелінійного елементу . Тому що цей відрізок характеризується нульовою швидкістю, тобто , а управління відсутнє , то відображаюча точка не може далі рухатися, і рух у системі закінчується.

Отже, відрізок осі абсцис, який належить до зони нечутливості, уявляє собою особливий відрізок врівноваженого стану системи, а кінцева точка руху буде залежати від початкових умов: .

В цілому фазові траєкторії приймають спіралевидну форму, що відповідає згасаючим коливальним процесам. Цей коливальний процес згасає не до нуля, а до деякого значення у інтервалі відрізка врівноваженого стану, тобто у середині зони нечутливості нелінійного елементу.

Приблизний фазовий портрет може бути знайдено за допомогою ізоклін та кутових коефіцієнтів .

Рівняння ізоклін приймають вигляд (2.115)

У середні зони нечутливості похил фазових траєкторій не залежить від значення зображаючої точки, а визначається лише значенням постійної часу , тобто має від'ємний похил 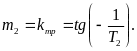(2.116).

Тому що фазові траєкторії не перетинаються, то зображаюча точка, вийшовши із початкової точки , буде послідовно перетинати ізокліни під відповідними кутами (Рис.3.14),створюючи відповідну фазову траєкторію.

Якщо при побудові фазової траєкторії зображаюча точка буде збільшувати свої координати та ,то процес буде розходитися, тобто система буде нестійкою.

Повний вигляд фазових траєкторій дає можливість визначити всі можливі властивості системи, тобто визначити фазовий портрет системи.

П 2. 18

Скласти математичну модель нелінійної системи

1. Визначається математична модель при

2. Визначаються змінні стану

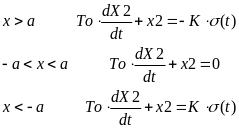
П 2.19

Для умов П 2.14 визначити фазовий портрет. Початкови умови при

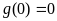
1. Рівняння на першому відрізку:

Кінцеві значення першої ділянці на лінії переключення

Рух від ображаючої точки на першої ділянці

2. Початвови умови на другої ділянці визначаються як кінцеві значення на першої ділянці. Рівняння другої ділянці мають вигляд

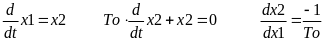
Кінцеві значення другої ділянці на лінії переключення

Рух від ображаючої точки по ділянкам

3. Початвови умови на третьої ділянці визначаються як кінцеві значення на другої ділянці. Рівняння третьої ділянці мають вигляд

Кінцеві значення першої ділянки на лінії переключення

Рух від ображаючої точки на третьої ділянці

4. Рівняння на четвертому відрізку визначається рівнянням на другої ділянці з початковими умовами, які визначаються кінцевими значеннями на третьому відрізку

Кінцеві значення четвертого відрізку визначаються умовами

Рух від ображаючої точки по ділянкам

2.4.6 Вплив нелiнiйностей на фазовий портрет нелiнiйної системи

Хай лiнiйна частина нелiнiйної системи визначається рівнянням (2.97), а нелiнiйнiсть має вигляд, який зображено на (Рис.2.48) вiдповiдно а, б, в, г.

Рис .2.56 До впливу нелінійностей на рух від ображаючої точки

Тому що при 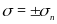рух у системi визначається рiвнянням (2.97) та відповідними початковими умовами , то фазовi траєкторії за цих умов будуть однаковi.

Але фазовий портрeт буде залежати вiд розташування на системi фазових координат лiнiй переключення. Отже, фазовi портрети будуть приймати вiдповiдний вигляд у залежностi вiд вигляду нелінійності

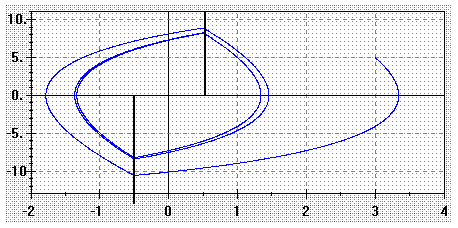
Рис.2.57 Вплив не лінійності на вигляд фазових траєкторій

Із розгляду фазових портретiв можна прийти до висновку, що вигляд нелiнiйностi суттєво змiнює динаміку протiкання перехiдних процесiв у нелiнiйних системах. Так нелiнiйнiсть типу двохпозицiйного iдеального реле приводить до зростання коливальності процесу. При цьому процес буде збiгатися до початку координат, але навiть у цьому випадку реле буде переключатися з великою швидкiстю, що є недоцiльним при використаннi таких систем. Реальнi трьох позиційні нелiнiйностi з петлею гістерезису (Рис.2.57 а) приводять до зменшення коливальності, але у деяких випадках залежно вiд зони гiстерезiсу може приводити до появи у системi незгасаючих коливань, тобто автоколивань при яких фазовi траєкторiї збiгаються до деякої замкненої траєкторiї, яка характеризується сталими параметрами i амплiтудою коливань, швидкiстю у точках переключення i отже, частотою. Такi замкненi траєкторiї визначають стiйкi граничні цикли. Поява петель гiстерезису (Рис.2.57в) приводить також до появи граничних цикл. При цьому при малих вiдхиленнях фазовi траєкторії будуть пiдходити до лiнiї граничного циклу з середини, що вiдповiдає нестiйкостi системи у малому, а при великих вiдхиленнях - iз зовнiшнього боку. Отже, у системi з такими нелiнiйностями теж виникають граничні цикли.