Лабораторна робота №7
Дослідження автоколивальних режимів у нелінійної системи
Призначення: Лабораторні дослідження націлені на закріплення знань основ аналізу нелінійних систем методом гармонічної лінеаризації, надання навичок застосування різноманітних методів розрахунків параметрів автоколивальних режимів, навичок експериментального аналізу, впливу місцевих зворотних зв’язків по швидкості.
Ціль роботи: Виявлення залежностей показників якості нелінійних систем у залежності від параметрів системи та особливостей ковзних режимів, і ефективності застосування місцевих зворотних зв’язків по швидкості.
Вибір структури САК виконується відповідно поставленої задачі експериментальних досліджень та аналізу функціональної схеми блока моделі узагальненої системи керування віртуального лабораторного стенду .Значення параметрів системи обираються з таблиці варіантів.
У лабораторній роботі необхідно:
- Побудувати математичну модель нелінійної системи та оцінити умови стійкості
- Розрахувати параметри автоколивань в залежності від заданого методу і оцінити умови стійкості автоколивальних режимів;
- Визначити умови абсолютної стійкості .
- Виконати експериментальні дослідження та побудувавши залежності параметрів автоколивань від Кр, То. Кс та зони нечутливості а.
- Оцінити можливість зриву автоколивань за рахунок місцевого зворотного зв’язку по швидкості.
- Оцінити можливість зриву автоколивань за рахунок вібраційної лінеаризації нелінійності.
- Визначити залежність еквівалентного коефіцієнта передачі нелінійного елемента від амплітуди вібраційного сигналу.
- Побудувати діаграми якості нелінійної системи у залежності від Кр, То, Кс
Висновок. Відповідно теоретичним розрахункам та обробки експериментальних досліджень зробити висновки згідно обраних цілей досліджень.
Тема 2.7 Математичні моделі систем керування у просторі стану
2.7.1 Векторно-матричні моделі систем керування
Процес функціонування
будь-якої системи будемо розглядати як
послідовність зміни її стану у деякому
інтервалі часу
.
Стан системи у кожний момент часу цього
інтервалу може характеризуватися
набором величин
.
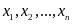При переході від одного миттєвого стану
до другого значення цих величин у
загальному випадку змінюється. Якщо
розглянемо процес функціонування
системи як послідовність зміни стану,
то
стають функціями часу
.
Величини
таким чином характеризують поведінку
системи у часі та називаються змінними
стану. Стан системи за допомогою цих
змінних можна інтерпретувати як
координати точки у n-мірному фазовому
просторі, кожному миттєвому стану
системи відповідає відповідна точка,
а процесу функціонування системи -
фазова траєкторія.
Фазова
траєкторія може бути описана вектор
функцією
.
Тому що моменту часу
відповідає деякий початковий стан
системи з характеристиками (початковими
умовами)
,
то під впливом зовнішніх збуджень
,
стан системи можна визначити як
.
Хай система автоматичного керування описується диференційним рівнянням n-го порядку вигляду
(2.241)
З теорії диференційних рівнянь відомо, що рішення рівняння (2.241) можна виразити у вигляді адитивної суми
(2.242)
де
- константи деяких n-лінійних незалежних
функцій
,
які є рішеннями диференційних рівнянь
першого порядку
, (2.243)
що витікають із (2.241).
Відомо, що
рішення однорідного диференційного
рівняння
є
,
де
– корені характеристичного рівняння
;
– функції, які виражають динаміку
процесів у системі, тобто змінні стану
системи для будь якого моменту часу
.
Отже, рівняння
(2.243) визначає рівняння змінних часу, а
(2.242) – рівняння виходу системи. Ці
змінні стану можуть бути використані
для визначення вихідного сигналу
системи керування:
(2.244)
Якщо система рівнянь є лінійною, то рівняння приймають вигляд:
,
.
Ці рівняння можуть бути записані у векторно-матрічній формі, тобто
,
(2.245)
де матриці
– матриці коефіцієнтів
,
,
,
,
які мають відповідну розмірність
.
Для стаціонарних систем матриці є сталими, а рівняння (2.242) приймають вигляд
,
, (2.246)
а векторно-матричну модель можна зобразити у вигляді:
Рис. 2.187 Узагальнена векторна матрична модель системи керування
При цьому матриця зветься матрицею коефіцієнтів,
– матрицею керування,
– матрицею виходу,
– матрицею обходу.
Якщо відомі
та початкові умови
,
то вихідний процес визначається
однозначно по
.Отже,
основною задачею при рішенні слідує
вважати задачу визначення змінних стану
.