
- •Тема 1.1. Загальні поняття та визначення …………………………………………………………… 19
- •Тема 1.2. Класифікація систем автоматичного керування ………………………………………35
- •Тема 1.3 Системний підхід до складання математичної моделі систем керування……. 66
- •Тема 1.4 Детерміновані сигнали та їх характеристики …………………………………… 89
- •Тема 2.1 Математичні моделі систем керування у вигляді диференційних рівнянь…….121
- •Тема 2.2 Передаточної функції неперервних систем керування…………………………..144
- •Тема 2.3 Стійкість процесів в неперервних системах керування………………………….. 164
- •Тема 2.4 Математичні моделі систем керування у фазовому просторі………………… 181
- •Тема 2.5 Математичні моделі систем керування за допомогою дискретних систем…… 220
- •Тема 2.6 Частотні характеристики систем автоматичного керування………………… 261
- •Тема 2.8 Задача визначення мінімуму середньо-квадратичної похибки…………………384
- •Тема 3.1 Методи підвищення якості систем керування……………………………………418
- •Тема 3.2 Типові лінійні закони керування………………………………………………….440
- •Тема 3.3 Синтез неперервних систем керування……………………………………………469
- •Тема 3.4 Методи синтезу дискретних систем керування ………………………………… 489
- •Тема 3.5 Синтез систем керування при дії випадкових збуреннях…………………………..511
- •Тема 3.6 Керованість та спостережливість систем керування…………………………….522
- •Тема 3.7 Поняття про оптимальне та адаптивне керування…………………………………554
- •Тема 1.1 Загальні поняття та визначення.
- •Основні поняття теорії автоматичного керування.
- •1.1.2 Основні задачі теорії автоматичного керування.
- •Основні поняття теорії автоматичного керування.
- •1.1.5 Підсистема керування (пристрій завдання, регулюючий пристрій, виконавчий пристрій, вимірювальні пристрої). Поняття типової ланки системи керування.
- •1.1.6 Система автоматичного керування та її основна задача
- •Тема 1.2 Класифікація систем автоматичного керування.
- •1.2.1 Класифікація систем керування за принципом організації (за принципом дії).
- •1.2.2 Принцип розімкненого керування.
- •1.2.3 Лабораторна робота №1
- •1.2.4 Принцип замкненого керування.
- •1.2.5 Лабораторна робота №2
- •1.2.6 Класифікація систем автоматичного керування за ціллю керування.
- •1.2.7 Класифікація систем автоматичного керування за математичним описом оператора системи.
- •1.2.8 Лінійні системи автоматичного керування.
- •1.2.9 Нелінійні системи автоматичного керування.
- •1.2.10 Класифікація нелінійностей
- •Наприклад: інерційна нелінійна ланка
- •1.2.11 Класифікація систем автоматичного керування за характером похибки у сталому режиму.
- •1.2.12 Класифікація за характером зміни оператора системи у часі.
- •1.2.13 Класифікація систем керування за кількістю каналів керування.
- •1.2.14 Класифікація систем керування за характером перетворення сигналів у часі.
- •1.2.15 Неперервні системи автоматичного керування.
- •1.2.16 Дискретні системи автоматичного керування.
- •1.2.17 Функції цифрового керування
- •1.2.18 Безпосереднє цифрове керування
- •1.2.19. Коректування впливу похибки перетворення аналогового сигналу у дискретний.
- •Тема 1.3 Системний підхід до складання математичних моделі систем керування.
- •1.3.1 Перетворення Лапласа
- •1.3.2 Властивості перетворення Лапласа.
- •1.3.4 Перетворення Фур’є .
- •1.3.5 Властивості перетворення Фур’є
- •1.3.6 Дискретне перетворення Лапласа.
- •Для вiдносного часу використовується символьна форма зображення
- •1.3.7 Основнi властивостi дискретного перетворення Лапласу
- •1.3.9 Основнi властивостi -перетворення
- •Вiдповiдно теорiї зсуву
- •Хай дискретне рiвняння має вигляд
- •Розглянемо основну смугу та видiлимо у неї контур 1-2-3-4-5-1.
- •Тема 1.4 Детерміновані сигнали та їх характеристики.
- •1.4.1 Неперервні сигнали.
- •1.4.2 Дискретні сигнали.
- •1.4.3 Випадкові сигнали та їх характеристики.
- •Типова кореляційна функція
- •1.4.4 Лабораторна робота №3
- •Іiнтегральна крива – рішення загального диференційного рівняння у вигляді деякої кривої у евклiдовому просторi
- •Кореляційна функція вихідного сигналу - визначається як
- •Кореляційна функція вихідного сигналу - визначається як
- •Тема 2.1 Аналіз неперервних систем керування за допомогою диференційних рівнянь.
- •2.1.1 Диференційні рівняння та методи їх розв’язання.
- •2.1.2 Застосування перетворення Лапласа до розв’язання диференційних рівнянь
- •2.1.3 Принцип лінеаризації рівнянь.
- •1.Виконується декомпозиція системи керування
- •2. Складаються рівняння елементів сак
- •2.1.4 Вагова (імпульсна) перехідна функція неперервних систем керування
- •2.1.5 Перехідна функція неперервних систем керування.
- •Оцінка якості перехідних процесів та задача аналітичного конструювання
- •2.1.7 Інтегральні показники якості перехідних процесів
- •Тема 2.2 Передаточні функції неперервних систем керування.
- •2.2.1 Передаточні функції типових ланок
- •2.2.2 Структурні перетворення передаточних функції.
- •2.2.3 Передаточні функції неперервних систем автоматичного керування.
- •2.2.4 Передаточні функції нестаціонарних систем
- •2.2.5 Зв'язок передаточної функції з часовими характеристиками
- •2.2.5 Зв'язок з часовими характеристиками
- •2.2.6 Точність систем керування у сталих режимах.
- •2.2.7 Статичні похибки систем керування.
- •2.2.8 Швидкісна ( кінематична ) похибка.
- •2.2.9 Похибка системи керування у сталих режимах.
- •2.2.10 Похибка системи керування при дії гармонічних впливів.
- •2.2.11 Компенсація збуджуючих впливів
- •2.2.12 Комбінована система керування по задаючому впливу
- •2.2.13 Комбіноване керування по збуджуючому впливу.
- •Тема 2.3 Поняття стійкості систем керування.
- •2.3.3 Достатні та необхідні умови стійкості неперервних систем керування
- •2.3.4 Теореми Ляпунова про стійкість лінійних систем керування
- •2.3.5 Алгебраїчні критерії стійкості.
- •2.3.6 Критерій Рауса.
- •2.3.7 Критерій Гурвіця.
- •2.3.8 Вплив параметрів системи керування на стійкість
- •2.3.9 Корневі методи оцінки якості перехідних процесів.
- •2.3.10 Визначення ступеня стійкості системи
- •2.3.11 Аналіз якості методом траєкторії коренів.
- •2.3.12 Вплив розташування нулів та полюсів передаточної функції на якість перехідних процесів.
- •2.4.1 Складання математично моделі нелінійної сау за функціональною схемою
- •2.4.2 Структурні перетворення нелінійних сау
- •2.4.4 Поняття змінних стану та фазового простору.
- •2.4.5 Опис систем керування на фазової площині.
- •Тоді диференційне рівняння фазової траєкторії приймають вигляд
- •2.4.8 Перехідні процеси у нелінійних системах.
- •2.4.9 Метод точкових перетворень.
- •2.4.11 Метод Лур’є – Поснікова
- •Тема 2.5 Математичні моделі систем керування за допомогою дискретних рівнянь
- •2.5.1 Дискретні рівняння систем керування та методи їх розв’язання.
- •Дійсно, хай дискретне рівняння має вигляд
- •Вільне рішення здобувається у вигляді (2.141)
- •2.5.2 Складання дискретних рівнянь лінійних систем
- •2.5.3 Вагова (імпульсна) перехідна функція дискретної системи.
- •Тому що у цифрових елементах управління виконується запам'ятання значення імпульсу на весь період квантування, то , бо . Отже, передаточна функція в цьому випадку буде
- •2.5.6 Властивостi w(z)
- •2.5.7 Передаточка функція умовно розімкнутої дискретної системи
- •Очевидно, що
- •2.5.8 Передаточнi функцiї замкнених дискретних систем
- •2.5.9 Умови стійкості дискретних систем керування.
- •Тому що рiшення дискретного рiвняння вiдшукується у виглядi , де вiльна складова, яка є рiшенням однорiдного рівняння
- •2.5.12 Критерій Джурі.
- •2.5.13 Оцінка точностi роботи дискретних систем у сталих режимах
- •2.5.14 Дослiдження швидкодiї та коливальностi дискретних систем управлiння
- •Тема 2.6 Частотні характеристики систем автоматичного керування
- •2.6.1 Комплексна функція передачі
- •2.6.2 Частотні характеристики систем керування з елементом чистої затримки
- •Систему, яка вiдповiдає цьому рiвнянню можна зобразити у виглядi
- •2.6.3 Зв’язок часових характеристик систем керування з їх частотними характеристиками. Визначимо зв'язок часових та частотних характеристик системи. Відомо, що
- •2.6.5 Частотнi характеристики дискретних систем
- •2.6.6 Логарифмічні характеристики неперервних систем керування.
- •2.6.7 Логарифмічні характеристики дискретних систем керування.
- •2.6.9 Принцип аргументу.
- •2.6.10 Критерій Михайлова.
- •2.6.13 Визначення стійкості по логарифмічним характеристикам.
- •2.6.15 Визначення стійкості систем керування з елементом чистої затримки.
- •2.6.17 Визначення областi стiйкостi у площинi одного параметру.
- •2.6.20 Визначення стійкості параметрів автоколивань у нелінійних системах
- •Запишемо характеристичне рiвняння замкненої системи у виглядi
- •2.6.26 Частотні методи дослідження якості
- •2.6.27 Показник коливальності систем керування
- •2.6.28 Зв’язок показників якості з частотними характеристиками
- •2.6.29 Оцінка якості перехідних процесів по логарифмічним характеристикам.
- •Лабораторна робота №6
- •Лабораторна робота №7
- •Тема 2.7 Математичні моделі систем керування у просторі стану
- •2.7.1 Векторно-матричні моделі систем керування
- •2.7.2 Методи вибору змiнних стану
- •2.7.3 Метод простих дробів.
- •2.7.4 Метод простих спiвмножникiв.
- •2.7.5 Метод нормальних змiнних стану.
- •2.7.6 Метод аналогового моделювання.
- •2.7.7 Метод структурного моделювання.
- •2.7.8 Нормальна форма рівняння.
- •2.7.9 Визначення перехідних процесів по векторно-матричним моделям.
- •2.7.9 Обчислення часових характеристик по векторно-матричним моделям.
- •При цьому
- •2.7.10 Визначення передаточної функції по вмм.
- •2.7.11 Визначення частотних характеристик з використанням векторно-матричної моделі системи
- •А розв’язок має вигляд (2.271)
- •2.7.12 Векторно-матричні моделі дискретних систем керування.
- •Якщо покласти , , то
- •2.7.13 Методи вибору змiнних стану для дискретних систем керування.
- •2.7.14 Метод розкладу на елементарнi дробi.
- •2.7.15 Метод нормальних змiнних стану. Нехай система описується дискретним рiвнянням
- •2.7.16 Складання вмм дискретної системи
- •2.7.17 Обчислення матричної експоненти exp(at) Тому що то суттєву роль у визначенні змiнних стану грає вираз який називають матрицею переходу або матричною експонентою.
- •Тодi рiшення рiвнянь стану записується у виглядi
- •Так, якщо задано цифрову систему керування , а матриця визначена як
- •Тому що
- •2.7.18 Визначення передаточної функції дискретної системи
- •2.7.19 Застосування вмм до аналізу нелінійних систем
- •2.7.20 Цифрове моделювання неперервних систем керування.
- •При цьому
- •2.7.21 Визначення стійкості по векторно-матричним моделям.
- •Тому що рiшення цього рiвняння добувається у виглядi
- •Лабораторна робота №8
- •Тема 2.8 Задача визначення мінімуму середньоквадратичної похибки
- •2.8.1 Лінійні перетворення випадкових сигналів.
- •2.8.3 Нелінійні перетворення випадкових сигналів
- •2.8.4 Статистична лінеаризація нелiнiйної ланки
- •2.8.5 Похибка системи керування при випадкових впливах.
- •2.8.6 Мінімізація похибки при заданої структури системи керування
- •2.8.7 Визначення дисперсії відхилення при випадкових впливах.
- •2.8.8 Критерії мінімуму середньоквадратичної похибки.
- •2.8.9 Визначення впливу змiни параметрiв системи на скв
- •2.8.10 Лабораторна робота №8 Дослідження впливу параметрів системи керування на мінімум середньо- квадратичні похибки.
- •Демпфірування з подавленням середніх частот -- процес зміщення вниз середньо частотної частини логарифмічної амплітудної частотної характеристики
- •Тема 3.1 Методи підвищення якості систем керування
- •3.1.1 Чутливість системи керування до зміни параметрів
- •3.1.2 Зміна параметрів систем керування за допомогою зворотних зв’язків.
- •3.1.3 Використання жорстких зворотних зв’язків
- •3.1.4 Використання гнучких зворотних зв’язків.
- •3.1.5 Використання неодиничних головних зворотних зв’язків.
- •3.1.6 Ковзні процеси у нелінійних системах керування.
- •3.1.7 Дослідження коливальних перехідних процесів у нелінійних системах керування.
- •3.1.8 Проходження повільно змінюючихся сигналів у автоколивальних нелінійних системах.
- •3.1.9 Вібраційна лінеаризація нелінійностей.
- •Тема 3 2 Типові лінійні закони керування.
- •3.2.1 Типові лінійні закони керування
- •3.2.2 Класифікація автоматичних регуляторів
- •3.2.3 Пропорційне керування
- •3.2.4 Інтегральні регулятори
- •3.2.5 Пропорційно-інтегральне керування.
- •3.2.6 Диференційні керуючі пристрої
- •3.2.7 Пропорційно інтегрально диференційні регулятори
- •3.2.8 Стандартні настройки контурів керування
- •3.2.9 Цифровий під-регулятор.
- •3.2.10 Лабораторна робота №7 Дослідження цифрового під регулятора.
- •3.2.11 Цифрові системи керування з кінцевим часом перехідного процесу
- •Тема 3.3 Синтез неперервних систем автоматичного керування.
- •3.3.1 Методи синтезу неперервних систем керування .
- •3.3.2 Побудова бажаної логарифмічної характеристики.
- •3.3.3 Синтез послідовного корегуючого пристрою.
- •3.3.3 Синтез корегуючого пристрою зворотнього зв’язку.
- •3.3.5 Корегуючі ланки та їх характеристики
- •3.3.6 Корекція нелінійних систем керування. Лінійна корекція нелінійних систем
- •3.3.7 Нелінійні корегуючі пристрої
- •Тема 3.4 Методи синтезу дискретних систем керування.
- •3.4.1 Послідовна корекція за допомогою аналогових пристроїв
- •Отже, .
- •3.4.2 Прямий синтез цифрових систем у області w-перетворень .
- •3.4.3 Корекція дискретних систем за допомогою регуляторів у колі зворотнього зв’язку.
- •Для умови z-перетворення записується у вигляді
- •3.4.4 Синтез цифрових регуляторів.
- •Отже, якщо
- •3.4.5 Реалізація цифрових регуляторів на цом.
- •3.4.6 Безпосереднє ( пряме ) програмування цр.
- •3.4.7 Послідовне програмування цр.
- •3.4.8 Паралельне програмування цр.
- •3.4.9 Синтез дискретних систем керування методом логарифмічних характеристик.
- •Тема 3.5 Синтез лінійних стаціонарних операторів при випадкових збудженнях.
- •3.5.1 Синтез лінійних стаціонарних операторів
- •3.5.2 Синтез при довільної структурі системи
- •3.5.3 Лабораторна робота №11
- •Тема 3.6 Керованість та спостережливість динамічних
- •3.6.1 Поняття керованості та спостережливості
- •3.6.2 Визначення умов досягаємості
- •3.6.3 Визначення умов керованості.
- •3.6.4 Визначення умов спостережливості
- •3.6.5 Визначення умов відновлюваності
- •3.6.6 Канонічні перетворення
- •3.6.7 Канонічна форма керованості
- •3.6.8 Канонічна форма відновлюваності
- •3.6.9 Канонічна форма спостережливості
- •3.6.8 Керованість замкнутох системи із зворотним зв’язком по стану
- •3.6.9 Дуальний зв’язок між канонічними формами
- •3.6.10 Оцінка вектору стану ( Спостерігаючи пристрої )
- •3.6.11 Спостерігач повного порядку
- •3.6.12 Синтез систем керування по заданому розташуванню полюсів за допомогою зворотного зв’язку по стану .
- •3.6.13 Синтез модальних регуляторів
- •3.6.14 Синтез цифрових систем керування із зворотнім зв`язком по стану
- •3.6.15 Застосування цифрового регулятора
- •3.6.16 Лабораторна робота №12
- •Тема 3.7 Поняття про оптимальне та адаптивне керування
- •Поняття про оптимальне та адаптивне керування
- •3.7.2 Критерії оптимальності
- •3.7.3 Класифікація задач оптимального керування
- •3.7.6 Метод класичного варіаційного числення.
- •Принцип максимуму Понтрягіна
- •3.7.8 Принцип максимуму для задачі із вільним кінцем траєкторії та із заданим часом керування.
- •3.7.9 Принцип максимуму для задач з незаданим часом керування.
- •3.7.10 Принцип максимуму в задачах оптимальної швидкодії з закріпленим кінцем траєкторії.
- •3.7.11 Теорема про інтервалах.
- •3.7.12 Застосування метода фазової площини для розв’язання задач оптимального за швидкодією керування.
- •3.7.13 Метод динамічного програмування. Принцип оптимальності Беллмана.
- •3.7.14 Дискретний варіант динамічного програмування.
- •3.7.15 Неперервний варіант динамічного програмування.
- •3.7.16 Системи екстремального керування
- •3.7.17 Методи визначення градієнта функції декількох змінних
- •3.7.18 Типи систем екстремального керування
- •3.7.19 Поняття про ідентифікацію
- •3.7.20 Адаптивні системи керування
- •3.7.21 Лабораторна робота №13
- •Література
- •Пункт Редагування
- •Пункт Вікно
- •Папки елементів
- •Елементи керування
2.4.9 Метод точкових перетворень.
Розглянемо рiвняння динамiки нелiнiйної системи, якi задано у виглядi
 (2.118)
(2.118)
Користуючись методом дослiдження нелiнiйної системи на фазової площинi представимо фазову траєкторію руху зображаючої точки.

Рис. 2.63 До постановки задачі точкових перетворень
На фазової площинi
![]() вiзьмемо
який-небудь вiдрiзок лiнiї
вiзьмемо
який-небудь вiдрiзок лiнiї
![]() ,
який перетинають фазовi траєкторії у
одному напрямку. Позначимо деяку точку
,
який перетинають фазовi траєкторії у
одному напрямку. Позначимо деяку точку
![]() фазової траєкторії, яка належить також
i лiнiї
фазової траєкторії, яка належить також
i лiнiї
![]() .
Очевидно, що зображаюча точка, рухаючись
по фазової траєкторії, через деякий час
знову прийде до лiнiї
,
але у точки
.
Очевидно, що зображаюча точка, рухаючись
по фазової траєкторії, через деякий час
знову прийде до лiнiї
,
але у точки
![]() .
Тому що точки
та
одночасно належать лiнiї
та фазової траєкторії, то мiж ними повинен
бути функцiональний взаємозв'язок
.
Тому що точки
та
одночасно належать лiнiї
та фазової траєкторії, то мiж ними повинен
бути функцiональний взаємозв'язок
![]() ,
,
який дозволяє по
попередньому значенню
знайти наступне
.
Далi, поклавши
новому початковому значенню знайти
наступну точку
![]() i так далi.
i так далi.
Отже, функцiональний взаємозв'язок
![]() ,
(2.119)
,
(2.119)
називається функцiєю послідовності, яка визначає закон точкових перетворень для даної нелiнiйної системи.
Очевидно, що якщо
![]() ,
то процес є згасаючим, а нелiнiйна система
є стiйкою.
,
то процес є згасаючим, а нелiнiйна система
є стiйкою.
Функцiя послідовності
може бути представлена у площинi
![]() деякою кривою
деякою кривою
![]() ,
а бiсектриса
,
а бiсектриса
![]() прямого кута буде лiнiєю точкового
перетворення точки
прямого кута буде лiнiєю точкового
перетворення точки
![]() самої у себе (Рис.2.64).
самої у себе (Рис.2.64).

Рис. 2.64 Функція точкових перетворень при визначенні режиму автоколивань
Очевидно, що точок
перетину бiсектриси
з функцiєю послiдовностi
визначає умови
![]() .
.
Умова
передбачає, що фазова траєкторія,
виходячи iз точки
![]() через деякий час знову пiдiйде до цiєї ж
точки, тобто фазовi траєкторії замкнуться
i у нелiнiйної системi утворюється
граничний цикл (точка
через деякий час знову пiдiйде до цiєї ж
точки, тобто фазовi траєкторії замкнуться
i у нелiнiйної системi утворюється
граничний цикл (точка
![]() ).
).
Треба визначити умови стiйкостi граничного циклу.
Тому що кутовий коефiцiєнт бiсектриси дорiвнює 1, тобто
![]()
то умови
 (2.120)
(2.120)
визначають умови
стiйкостi граничного циклу. Дiйсно,
послiдовне перетворення зображаючої
точки
у
![]() показує що процес буде сходитися у точку
як справа, так i злiва.
показує що процес буде сходитися у точку
як справа, так i злiва.
Якщо
(2.121)
то це свiдчить про умови нестiйкостi граничного циклу.
Якщо сумiсного рiшення немає, а функцiя послідовності знаходиться нижче бiсектриси , то це вказує на стiйкiсть нелiнiйної системи.
Якщо функцiя Т розташована вище бiсектриси, то у нелiнiйної системи спостерiгаються розбіжні процеси, тобто система буде нестiйкою (Рис.2.65).

а) б)
Рис.2.65 Приклади нестійких а) автоколивань та б) стійких і нестійкиї процесів
Функцiя послідовності знаходиться на пiдставi рiшення рiвнянь динаміки
та на визначеннi лiнiї точкових перетворень.
Так, у випадку
релейних характеристик нелiнiйностi у
якостi лiнiї
на фазовій площинi може бути подана сама
лiнiя переключень, на якій одна iз координат
( тобто
![]() )
визначена через математичну модель
нелiнiйностi.
)
визначена через математичну модель
нелiнiйностi.
Очевидно, що при
цьому, якщо модуль швидкостi
![]() у точцi
буде меншою нiж у точцi
,
то процес є згасаючим.
у точцi
буде меншою нiж у точцi
,
то процес є згасаючим.
Функцiю послідовності
можна визначити, якщо виразити координати
зображаючої точки
![]() через
початковi координати
через
початковi координати
![]() .
.
Знаходячи
вiдповiднi рiшення на iнтервалах по
початковим умовам та постiйним iнтегрування
![]() ,
,
![]() ,
,![]() ,
можна визначити функцiональний зв'язок
,
можна визначити функцiональний зв'язок
![]() ,
який i буде функцiєю послідовності.
,
який i буде функцiєю послідовності.
Якщо у явної формi
визначити функцiю послідовності
неможливо, то її визначають у параметричному
виглядi. При цьому параметрична форма
точкового перетворення буде мати
параметр часу
![]() , за який зображаюча точка проходить по
фазової траєкторії вiд точки
до
.
, за який зображаюча точка проходить по
фазової траєкторії вiд точки
до
.
Через цей параметр на основi рiвнянь динаміки виражаються координати точок та
![]()
![]() (
2.122)
(
2.122)
та будуються графiки цих функцiй (Рис.2.66).

Рис. 2.66 До задачі визначення функції послідовності
Точка їх перетинання
дає умови
![]() ,
i, отже, координату
,
i, отже, координату
![]() замкненої
траєкторії, а також визначає перiод
вiдповiдних автоколивань.
замкненої
траєкторії, а також визначає перiод
вiдповiдних автоколивань.

Рис. 2.67 Параметричне визначення режиму автоколивань
Хай динаміка нелінійної системи описується рiвнянням
![]()
для даного випадку при
![]()
рiвняння фазової траєкторії визначаються як

Вiдкiля
![]()
Тому що у точцi
![]() значення
значення
![]() ,
то
,
то
![]()

Для iнтервалу, де
виконуються умови
![]() рiвняння динаміки приймає вигляд
рiвняння динаміки приймає вигляд
![]() а початкові умови визначаються як
а початкові умови визначаються як
![]() ,
,![]() .
.
Отже,

Тому що у точцi![]() ,
то
,
то


Рис. 2.68 До визначення функції точкових перетворень в нелінійної системі з непарно-симетричною нелінійностю
При пiдстановці
(3.65) у ( 3.64 ) здобудемо
![]()


Отже,

Використовуючи
t як параметр можна побудувати
залежнiсть
![]() .
.

Рис. 2.69 Параметричне розв’язання задачі
Із графiка (Рис.2.69) видно, що динаміка системи має згасаючий характер, тобто у системi не спостерiгаються автоколивання, а сама система є стiйкою.
Розглянемо нелiнiйну систему, яка має рiвняння руху у виглядi
![]()
а
![]() задано
у виглядi реле з петлею гістерезису
Рис.2.70
задано
у виглядi реле з петлею гістерезису
Рис.2.70

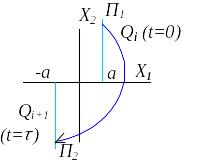
Рис. 2.70 Нелінійність з гістерезисом Рис. 2.71 До задачі визначення функції Т
Вiдомо, що
рiшення на фазової площинi
![]() буде мати вигляд (Рис.2.71) з лiнiями
переключення
буде мати вигляд (Рис.2.71) з лiнiями
переключення
![]() .
Будемо розглядати точкове перетворення
півпрямої
.
Будемо розглядати точкове перетворення
півпрямої
![]() у півпряму
у півпряму
![]() з початкової точки
у наступну
.
Тому що
при
з початкової точки
у наступну
.
Тому що
при
![]() визначається координатами
визначається координатами![]() ,
то закон перетворення будемо шукати у
параметричному виглядi
,
то закон перетворення будемо шукати у
параметричному виглядi
![]() та
та![]() .
.
Отже, на першому iнтервалi рух зображаючої точки буде здiйснюватися вiдповiдно рiвнянь
 ,
,
а значення координат на кiнцi iнтервалу, тобто у точцi , буде мати вигляд
 .
.

Рис. 2.72 Параметричний метод визначення параметрів автоколивань
Вiдкiля рiвняння параметричного закону точкових перетворень (Рис. 2.72) будуть
 ,
,

2.4.10 Другий (прямий) метод Ляпунова
Із теорії дослідження стійкості лінійних систем відомі теореми першого методу Ляпунова, які дозволяють визначити умови збіжності по лінеаризованим рівнянням, коли поведінка системи розглядається поблизу робочої точки при малих відхиленнях.
Згадаємо стисло постановку задачі дослідження стійкості по першому методу Ляпунова.
Хай задано зведені до нормальної форми Коші диференційні рівняння системи
 (2.123)
(2.123)
Будемо
вважати, що при визначеної сукупності
початкових умов
 є єдине рішення системи рівнянь
є єдине рішення системи рівнянь
 .
.
Хай
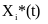 позначає
деякий сталий процес, який приймемо за
незбуджений рух. Всякий другий рух
визначається збудженим, а відхилення
збудженого руху від незбудженого дає
можливість визначити нульове рішення
позначає
деякий сталий процес, який приймемо за
незбуджений рух. Всякий другий рух
визначається збудженим, а відхилення
збудженого руху від незбудженого дає
можливість визначити нульове рішення

при
якому незбуджений рух
 визначає асимптотичну стійкість.
визначає асимптотичну стійкість.
Геометричний
образ незбудженого руху
 системи
n-ого порядку можна представити
умовно у вигляді деякої інтегральної
кривої у n-мірному простору з додатковою
віссю часу
(
Рис. 2.73).
системи
n-ого порядку можна представити
умовно у вигляді деякої інтегральної
кривої у n-мірному простору з додатковою
віссю часу
(
Рис. 2.73).


Рис. 2.73 Рис.2.74
Збуджений
рух
буде
визначатися другою кривою, а різниця
між ними дає відхилення
 .
У відхиленнях
.
У відхиленнях
 ,
тобто у просторі координат стану системи
ця картина збудженого руху буде виглядати.
Рівняння
,
тобто у просторі координат стану системи
ця картина збудженого руху буде виглядати.
Рівняння
 називається станом рівноваги. Якщо для
лінійних систем мається один стан
рівноваги, а стійкість розглядається
як асимптотична, то для нелінійних
систем можуть з'являтися деякі області
стійких та нестійких станів рівноваги.
називається станом рівноваги. Якщо для
лінійних систем мається один стан
рівноваги, а стійкість розглядається
як асимптотична, то для нелінійних
систем можуть з'являтися деякі області
стійких та нестійких станів рівноваги.
При цьому .
В цьому випадку відхилення будуть прагнути не до нульових значень, а до деякої постійної величини
 (
2.124 )
(
2.124 )
Отже,
незбуджений рух системи називається
сталим, якщо задав "трубку" скільки
завгодно малого n-мірного перетину
,
можна добрати у початковий момент часу
 таку
область початкових умов , яка залежить
від
,
що із збільшенням часу
збуджений
рух
таку
область початкових умов , яка залежить
від
,
що із збільшенням часу
збуджений
рух
 через
деякий час не буде виходити із заданої
трубки
(Рис.2.75).
через
деякий час не буде виходити із заданої
трубки
(Рис.2.75).

Рис .2.75
Таким
чином, незбуджений рух системи називається
стійким, якщо при заданому
скільки б воно мале не було, існує таке
,
що при початкових умовах
 у подальшому руху
у подальшому руху
 виконуються умови
.
виконуються умови
.
Якщо
умови стійкості виконуються при
будь-якому характері нелінійної
залежностi
 всередині
визначеного класу нелiнiйностей, то
стiйкiсть вважається абсолютною.
всередині
визначеного класу нелiнiйностей, то
стiйкiсть вважається абсолютною.
Розглянемо тепер суть другого ( прямого ) метода Ляпунова.
Для
визначення стiйкостi нелiнiйних систем,
треба розглядати рух зображаючої точки
у n-мiрному просторi
 .
.
Хай
мається функцiя декiлькох змiнних

у
n-мiрному просторi. Отже, у кожної точки
даного простору функцiя
 визначена
та має одне значення.
визначена
та має одне значення.
Якщо функцiя у всiх точках деякої областi навколо координат зберiгає один i той же знак та нiде не перетворюється у нуль, крiм тiльки самого початку координат, то така функцiя називається знаковизначеною.
Функцiя називається знакопостійною, якщо вона зберiгає один i той же знак, але може перетворитися у нуль не тiльки у початку координат, але i у других точках розглянутої областi.
Якщо ж функцiя може мати рiзнi знаки у даної областi навколо початку координат, то вона називається знакозмінною.
Так
для тривимірного простору
 функцiя
функцiя
 при умовах
при умовах
 буде знакозмінною,
буде знакозмінною,
 при умовах
при умовах
 ,
буде знакопостійною. Тодi як при
,
буде знакопостійною. Тодi як при
 є знаковизначеною, тому що вона володіє
умовами
є знаковизначеною, тому що вона володіє
умовами
 тiльки
при
тiльки
при
 .
.
Другий метод Ляпунова, який вiдомий пiд назвою прямого метода, засновано на розгляданнi поведiнки спецiальної функцiї ( функцiї Ляпунова ) навколо початку координат у областi параметрiв стану.
Будь-яку
функцiю ,
яка тотожно перетворюється у нуль
,
при
,
яка тотожно перетворюється у нуль
,
при
 будемо
називати функцiєю Ляпунова, якщо у неї
у якостi величин
взяти
вiдхилення змiнних стану системи
управлiння у перехiдному процесi
будемо
називати функцiєю Ляпунова, якщо у неї
у якостi величин
взяти
вiдхилення змiнних стану системи
управлiння у перехiдному процесi

у
яких записуються рiвняння для цiєї
системи
 .
.
Щоб розглянути динаміку протiкання процесу у часi, треба визначити похiдну функцiї Ляпунова у часi

тобто

Отже, похiдна також є даною функцiєю координат стану системи
 (
2.125 )
(
2.125 )
Розглянемо
 ,
як вектор швидкостi зображаючої точки
у
фазовому просторi.
,
як вектор швидкостi зображаючої точки
у
фазовому просторi.
Тому
що
 а
а
 є проекцiєю на осi координат, та визначає
градiєнт функцiї
то
є проекцiєю на осi координат, та визначає
градiєнт функцiї
то
 (
3.126 )
(
3.126 )
Отож, похiдна функцiї Ляпунова у часi, яку складено у силу рiвнянь системи, представляє собою скалярний добуток градiєнту цiєї функцiї на вектор фазової швидкості.
Якщо функцiя
визначена
як деяка поверхня навколо почата
координат, то вектор
 перпендикулярний
до даної поверхнi
перпендикулярний
до даної поверхнi
 та спрямовує у бiк збiльшення значень
.
Очевидно, що якщо похiдна
та спрямовує у бiк збiльшення значень
.
Очевидно, що якщо похiдна
 ,
то фазовi траєкторії перетинають
поверхню
,
то фазовi траєкторії перетинають
поверхню
 у сторону збiльшення значень
.
у сторону збiльшення значень
.
Якщо ж
 (3.127)
(3.127)
то
фазові траєкторії йдуть у бік зменшення
.
Таким чином, якщо для системи
 iснує знаковизначена функцiя
,
похiдна вiд якої є знакопостійною
протилежного знаку, рiшення системи
iснує знаковизначена функцiя
,
похiдна вiд якої є знакопостійною
протилежного знаку, рiшення системи
 стiйке.
стiйке.
Розглянемо геометричну інтерпретацію даного формулювання.
У
фазовому просторi координат хi мається
функцiя
 ,
яка зображає замкнену поверхню та
охоплює точку рівноваги
,
яка зображає замкнену поверхню та
охоплює точку рівноваги
 .
Поверхня
.
Поверхня
 буде
знаходитися всерединi поверхнi
буде
знаходитися всерединi поверхнi
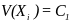 ,
якщо
,
якщо
 .
При наближеннi всiх хi до
нулю,
.
При наближеннi всiх хi до
нулю,
 також наближаються до нулю, тобто
поверхня стягується у точку
також наближаються до нулю, тобто
поверхня стягується у точку
 .
Якщо похiдна вiд функцiї Ляпунова буде
знаковизначеною та вiд'ємною, тобто якщо
.
Якщо похiдна вiд функцiї Ляпунова буде
знаковизначеною та вiд'ємною, тобто якщо
 у всiх точках досліджуваного фазового
простору крiм одного тiльки початку
координат, де
у всiх точках досліджуваного фазового
простору крiм одного тiльки початку
координат, де
 , то при будь яких початкових умовах
зображаюча точка
, то при будь яких початкових умовах
зображаюча точка
 буде
асимптотично рухатися у бiк зменшення
.
Тому що
зменшується, то це позначає, що з протягом
часу фазовi траєкторії пронизують
замкненi поверхнi
,
переходячи iз зовнiшнiй поверхнi на
внутрiшнi, та, у кiнцевому пiдсумку,
стягуються до точки рiвноваги.
буде
асимптотично рухатися у бiк зменшення
.
Тому що
зменшується, то це позначає, що з протягом
часу фазовi траєкторії пронизують
замкненi поверхнi
,
переходячи iз зовнiшнiй поверхнi на
внутрiшнi, та, у кiнцевому пiдсумку,
стягуються до точки рiвноваги.

Рис. 2.76
Якщо ж функцiя
 буде
знакопостійною, то траєкторія зображаючої
точки
,
буде застрявати на деякої поверхнi
буде
знакопостійною, то траєкторія зображаючої
точки
,
буде застрявати на деякої поверхнi
 ,
тому що
,
тому що
 у цих областях перетворюється у нуль.
В цьому випадку рух вважається тiльки
стiйким. Таким чином, задачу по дослiдженню
стiйкостi нелiнiйної системи можна звести
до задачі визначення функції Ляпунова
та оцінки знаку її похiдної.
у цих областях перетворюється у нуль.
В цьому випадку рух вважається тiльки
стiйким. Таким чином, задачу по дослiдженню
стiйкостi нелiнiйної системи можна звести
до задачі визначення функції Ляпунова
та оцінки знаку її похiдної.
Задача про знаходження функцiї Ляпунова складна та зв'язана з великими математичними труднощами. Слiдує вiдмiтити, що якщо функцiю Ляпунова не можна знайти, то це ще не позначає, що система нестiйка.
Якщо
система описується рiвнянням вигляду
 ,
то для того щоб оцiнити стiйкiсть системи
треба щоб виконувалася умова
знакопостійності, а для цього функцiя
Ляпунова повинна виражатися у квадратичних
формах
,
то для того щоб оцiнити стiйкiсть системи
треба щоб виконувалася умова
знакопостійності, а для цього функцiя
Ляпунова повинна виражатися у квадратичних
формах
( 2.128 )
або у матричних формах
( 2.129 )
де

Тодi
 (2.130 )
(2.130 )
Якщо матриця Q додатно визначена, то
 (
2.131)
(
2.131)
коли
 ,
тобто виконується зменшення функцiї
,
а отже, траєкторії системи збiгаються
до початку координат. Отож,
якщо одночасно виконуються нерiвностi
та
,
тобто виконується зменшення функцiї
,
а отже, траєкторії системи збiгаються
до початку координат. Отож,
якщо одночасно виконуються нерiвностi
та
 у деякої областi простору змiнних
у деякої областi простору змiнних
 включаючи початок координат, то положення
рiвноваги у початку координат асимптотично
стiйке.
включаючи початок координат, то положення
рiвноваги у початку координат асимптотично
стiйке.
Хай лінійна система керування описується системою рівнянь


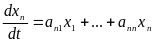
або

Хай дана система


Для
того, щоб визначити умови, якi накладаються
на функцiї
 при яких нульове рiшення системи буде
стiйке, функцiя Ляпунова повинна бути
знакопостійною.
при яких нульове рiшення системи буде
стiйке, функцiя Ляпунова повинна бути
знакопостійною.
Отже,
 .
.
Таким чином на розглядуваній кривій функцiя V(х1х2) перетворюється у функцiю аргументу часу t, що дозволяє визначити похiдну.

Функцiя V представляє собою квадрат вiдстанi вiд iнтегральної кривої до початку координат. Тому нульове рiшення цiєї системи буде явно стiйким, якщо ця вiддаль монотонно зменшується при . Для цього потрiбно, щоб виконувались умови
 при
при
 .
.
Отже,
якщо
 ,
то перетворивши вираз
,
то перетворивши вираз

де
 .
.
Одержимо
умови стiйкостi системи
 .
.
Хай система автоматичного управлiння описується рiвнянням

Функцiю
Ляпунова виберемо у вигляд

Тодi

Для
стiйкостi системи, тобто для виконання
умов
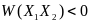 треба, щоб виконувалась
треба, щоб виконувалась
 .
.
Квадратична форма або матриця є додатно визначеною, вiд'ємно визначеною, знакододатною, знаковiд'ємною, невизначеною або тотожно рiвною нулю тiльки i тiльки у тому випадку, якщо властивi значення матрицi , якi для симетричної матрицi дiйснi, вiдповiдно всi додатнi, всi вiд'ємнi, всi невiд'ємнi, всi не додатнi, мають рiвнi знаки або всi дорiвнюють нулю.
Очевидно, що на пiдставi виразу
 ( 2.122 )
( 2.122 )
можна визначити через криволiнiйний iнтеграл
 (
2.123 )
(
2.123 )
функцiю
Ляпунова
 Вiдомо,
що скалярна функцiя
визначається iз криволiнiйного інтегралу
вiд вектора
Вiдомо,
що скалярна функцiя
визначається iз криволiнiйного інтегралу
вiд вектора
 у тому випадку, якщо
не залежить вiд шляху iнтегрування. Для
цього ж необхiдно i достатньо, щоб
виконувалися умови
у тому випадку, якщо
не залежить вiд шляху iнтегрування. Для
цього ж необхiдно i достатньо, щоб
виконувалися умови
 (
2.124 )
(
2.124 )
де
 – i-та складова градiєнту
– i-та складова градiєнту

В цьому випадку
 ( 2.125 )
( 2.125 )
Хай
система описується диференцiйним
рiвнянням
 або рiвнянням у змiнних стану
або рiвнянням у змiнних стану

Визначимо градiєнт функцiї Ляпунова у виглядi

та будемо шукати похiдну вiд функцiї Ляпунова у виглядi

Якщо
прийняти
 ,
здобудемо
,
здобудемо

Якщо
 ,
то
,
то
 i
для виконання умови
i
для виконання умови
 повинно виконуватись
повинно виконуватись
 .
.
При цьому

Функцiя Ляпунова може бути визначена по криволiнiйному інтегралу

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
P.S.

для незалежностi вiд шляху iнтегрування повинна виконуватись умова

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Відомо,
що канонічною формою рівняння


 зветься такий їх вигляд, коли матриця
зветься такий їх вигляд, коли матриця
 приведена до жорданового вигляду.
Зробимо заміну
приведена до жорданового вигляду.
Зробимо заміну

 .
Тоді
.
Тоді
 ,
,
 ,
де
,
де
 .
.
Зробимо
заміну
 .
При цьому
.
При цьому

 буде визначати канонічну форму
рівняння руху.
буде визначати канонічну форму
рівняння руху.
Для
того, щоб стану рівноваги
 системи відповідав єдиний стан
рівноваги
системи відповідав єдиний стан
рівноваги
 необхідно, щоб визначник системи не
дорівнював нулю, тобто щоб виконувалася
умова
необхідно, щоб визначник системи не
дорівнював нулю, тобто щоб виконувалася
умова
 або
або
 . Якщо врахувати, що
. Якщо врахувати, що
 ,
,
 ,
,
 ,
будемо мати
,
будемо мати
 .
.
