1.3.9 Основнi властивостi -перетворення

1. Властивiсть лiнiйностi – зображення лiнiйної комбiнацiї дискретних функцiй дорiвнює тій самій лiнiйній комбiнацiї їх зображень.

Хай

Тодi

2. Теорема зсуву.

Розглянемо функцiю запізнення , тобто яка має зсув на цiле число тактiв .

Якщо покласти то

Якщо вихідна функцiя при вiд'ємних значеннях аргументу дорiвнює нулю, то

(1.70)

Якщо зсув виконується праворуч (упередження), то

3. Зображення рiзниць.

Вiдповiдно теорiї зсуву

.

При нульових початкових умовах

Аналогiчно,

Зазначимо, що при (неперервнi системи)

,

що iлюструє схожiсть зображень похiдних та рiзницi.

4. Кiнцеве значення дискретної функцiї.

Визначимо зображення першої прямої рiзницi функцiї

Знайдемо суму ординат

(1.71)

Тому що ,

а при , , то

Таким чином (1.72)

Порiвнюючи вирази (2.14) та (2.15) для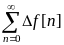 здобудемо 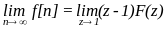(1.73) (1.73)

5. Зв'язок дискретних рівнянь з їх -зображеннями.

Хай дискретне рiвняння має вигляд

Згiдно теореми зсуву запишемо

Тодi

(1.74)

Вивчення вiдносин мiж та - площинами при перетвореннi є важливим у зв'язку з можливостями аналiзу розташування нулiв та полюсiв передаточної функцiї системи на вiдповiдних площинах.

Розглянемо основну смугу та видiлимо у неї контур 1-2-3-4-5-1.

Рис. 1.81 Співвідношення основної смугг до одиничного кола

Тому що

, (1.75)

то всi додатковi смуги півплощині -площини вiдображаються у теж саме одиничне коло на -площинi, а всi точки, якi належать вiдповiдному контуру, якi вiдображуються усередину одиничного кола.

Лiнiї на - площинi, якi паралельнi уявної осi, тобто лiнiї сталого загасання для неперервних систем, вiдображаються на -площинi колом радiусу ( Рис1.82)

Рис. 1.82 Співвідношення лінії сталого згасання

Для будь-якої лiнiї на -площинi на -площинi буде вiдповiдати лiнiя, яка виходить iз початку координат пiд кутом рад.

П 1.13

Визначити інтервал дискретності , при якому ступінчатий опис функції по дискретним точкам не приведе до похибки не більше ніж 5% початкового значення.

• Найбільша крутизна заданої функції спостерігається у точці

Початкове значення 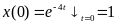. На першому інтервалі .

Відкіля

П. 1.14

Для експоненціальної функції визначити інтервал дискретності , при якому лінійна інтерполяція значень функції у середині проміжків між дискретними точками не перевищує 1% початкового значення.

• На першому інтервалі для середини відрізку дає , тоді як фактичне значення для буде . Отже,

П 1.15

Для експоненціальної функції визначити - перетворення

Тому що , а перетворення Лапласа

, то з урахуванням . Отже,

.

Для 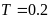та .

П 1.16

Для при знайти зворотне - перетворення

Для цього треба розкласти по від’ємним степеням

.

П 1.17

Приклад переходу від перетворення Лапласа до перетворення

Задано оператор з фіксатором нульового порядку на вході

1. Визначається зворотне перетворення

2. Визначається перетворення

3. Додається співмножник та спрощується вираз для

3. Спрощується результат

або

3. Визначається перехідний процес

3. Порівняння перехідних процесів дискретного та неперервного

П 1.18

Приклад переходу від перетворення до дискретного перетворення Лапласа та побудови амплітудо-частотної характеристики

Процеси мiж моментами квантування (Метод модифікованого - перетворення). Метод - перетворення ефективний для систем, у яких сигнали можуть бути адекватно представленi їх вибiрками у моменти квантування. Якщо ж ця умова не виконується, то необхiдно визначити реакцiю системи мiж моментами квантування.

Припустимо, що треба визначити перехiдний процес мiж моментами квантування для системи, яка показана на Рис. 1.83

Рис. 1.83 Вибiрка між моментами квантування

З'єднаємо вихід з блоком фiктивної затримки на час , тобто , на виходi якого сигнал буде , дискретне значення якого здобудемо за допомогою дискретного квантування. Час затримки може лежати у межах перiоду квантування (Рис. 2.8).

Рис. 1.84 Період квантування та час затримки

Тоді ,

а

Для обчислення модифiкованого - перетворення можна користуватися формулами

, (1.76)

де вичети знаходяться за всiма полюсами зображення сигналу .

Так для

при

Для

Таблиця

Таблиця співвідношення оригіналів та їх зображень.

Оригінал	дискретний
		1	1

1.3.10 W-перетворення

Вiдомо, що у зв'язку iз застосуванням - перетворення основна смуга - площини у межах частот

вiдображається у коло одиничного радiусу на комплексної площинi .

Із теорiї перетворень вiдомо, що коло одиничного радiусу може бути розгорнуто у площину на основi бiлiнiйного перетворення, яке використовує замiну комплексної змiнної на

(1.77)

Якщо подальше використати підстановку , то при цьому здобудемо

(1.78)

де

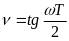
визначає вiдносну псевдочастоту.

При цьому коло одиничного радiусу у - площинi перетворюється у уявну вiсь - площини.

Рис. 1.85 До білінійного перетворення

Замiсть вiдносної псевдочастоти можна ввести пропорцiйну величину :

(1.79)

яка називається абсолютною псевдочастотою. При такій замiнi лiвій напiвплощині у межах

(1.80)

вiдповiдає уся лiва півплощина комплексної змiнної , а перехід вiд -зображення виконується шляхом замiни

(1.81)

Тому що при умовах, коли аргумент функції тангенсу менше одиниці

то у цьому дiапазонi виконуються умови .

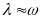Отже, якщо виконуються умови то можна псевдочастоту замiнювати дiйсною частиною, що приводить до значного спрощення обчислень. При цьому у межах

псевдочастота змiнюється у дiапазонi

(1.82)

а комплексна величина перемiщується по уявнiй осi вiд до .