
- •В.И. Родионов
- •Теория автоматического управления Конспект лекций
- •Часть 1
- •Введение ……………………………………………………….……………….…5 в.1. Значение автоматического управления и задачи курса………….………5
- •Лекция 2
- •Основные понятия и определения тау
- •Функциональные элементы сау
- •Классификация систем автоматического
- •1.3. Примеры систем автоматического управления
- •2. Математическое описание сау
- •Вынужденное движение и собственные колебания системы. Переходный и установившийся режимы
- •2.3. Передаточные функции
- •2. Типовые звенья сау.
- •2.4. Переходная характеристика и весовая функция
- •Типовые звенья систем автоматического
- •2.6. Неустойчивые и неминимально–фазовые звенья
- •1. Структурные схемы сау.
- •3. Передаточные функции замкнутой и разомкнутой системы.
- •2.7. Структурные схемы сау
- •2.8. Составление и преобразование структурных схем сау
- •2.9. Передаточные функции замкнутой и разомкнутой
- •Установившиеся режимы
- •Точность сау в установившемся режиме.
- •Установившиеся ошибки следящих систем.
- •3.1. Точность сау в установившемся режиме
- •3.2. Установившиеся ошибки следящих систем
- •Частотные характеристики сау.
- •Частотные характеристики сау
- •Логарифмические амплитуднные и фазовые
- •3.5. Частотные характеристики типовых звеньев
- •3.6. Особенности частотных характеристик устойчивых
- •4. Устойчивость систем автоматического управления
- •Определение устойчивости по Ляпунову.
- •Критерий устойчивости Гурвица.
- •4.1. Общие понятия об устойчивости заданного режима
- •4.2. Определение устойчивости по а.М. Ляпунову
- •3. Критерий устойчивости гурвица
- •Таким образом, кроме положительности коэффициентов а30; а20; а10; а00
- •4.4. Критерий михайлова
- •4.5. Критерий найквиста
- •4.6. Суждение об устойчивости по лафчх
- •4.7. Выделение областей устойчивости
- •Суждение об устойчивости системы по ее линейной модели.
- •Суждение об устойчивости системы
- •5. Качество сау
- •5.1. Основные показатели качества
- •5.2. Методы построения переходных процессов
- •Преобразования Фурье имеют вид:
- •5.2.1 . Частотный метод анализа качества сау,
- •Приближенный метод построения кривой переходного процесса с помощью трапециидальных частотных
- •Лекция 14
- •5.3. Построение вещественной частотной характеристики замкнутой системы по частотным характеристикам
- •План лекции:
- •5.5. Косвенные оценки качества, связанные с распределением нулей и полюсов передаточной функции
- •5.7. Интегральные оценки качества
- •5.8. Косвенные оценки качества, связанные с видом
- •5.8.1. Анализ качества по ачх замкнутой системы
- •5.8.2. Оценка качества сау по логарифмическим частотным
- •Приближенная оценка вида переходного процесса
- •6. Динамический синтез сау
- •Методы коррекции динамических свойств сау.
- •6.1. Общие понятия синтеза сау
- •6.2. Этапы синтеза сау
- •6.3. Требования, предъявляемые к динамическим
- •Методы коррекции динамических свойств сау.
- •6.5. Методы коррекции динамических свойств системы,
- •6.5. Динамический синтез сау, основанный
- •Синтез последовательного корректирующего устройства.
- •Синтез параллельного корректирующего устройства.
- •6.6. Синтез последовательного корректирующего устройства
- •6.7. Синтез параллельного корректирующего устройства
- •7. Методы синтеза, основанные на теории
- •7.1. Уравнения системы в пространстве состояний
- •7.2. Коррекция системы в пространстве состояний
- •7.3. Прямой корневой метод синтеза
- •7.4. Прямой корневой метод синтеза сау
- •7.5. Прямой метод синтеза корректирующей обратной
- •Лекция 22
- •8.2. Основные вероятностные характеристики
- •8.2.1. Функция распределения и плотность вероятности
- •8.2.2. Математическое ожидание, дисперсия
- •8.3. Стационарные случайные процессы.
- •8.3.1. Стационарные случайные процессы
- •8.3.2. Эргодические случайные процессы
- •Спектральная плотность стационарного
- •8.5. Свойства корреляционных функций и спектральных плотностей стационарных эргодических
- •8.6. Статистические характеристики случайных
- •8.6.1. Белый шум
- •8.6.2. Корреляционная функция и спектральная плотность скорости изменения азимута
- •8.6.3. Спектральная плотность задающего воздействия системы наведения ракеты на цель
- •8.7. Экспериментальное определение корреляционных функций, спектральных плотностей и дисперсий
- •8.8. Прохождение случайных воздействий
- •8.8.1. Интегральное Уравнение связи
- •8.8.2. Спектральное уравнение связи
- •8.8.3. Определение динамических характеристик сау
- •8.9. Методы определения ошибок линейных сау,
- •8.9.1. Эквивалентное представление стационарного
- •8.9.2. Расчет флуктуационных ошибок и ошибок
- •8.9.3. Графоаналитический метод расчета
- •8.9.4. Оценка флуктуационных ошибок, обусловленных
- •8.9.5. Расчет дисперсии помехи с помощью
- •8.9.6. Вычисление среднеквадратической ошибки
-
Вынужденное движение и собственные колебания системы. Переходный и установившийся режимы
В общем виде движение линейной САУ с постоянными параметрами описывается дифференциальным уравнением n-го порядка с постоянным коэффициентами
anx(n)+an-1x(n-1)+…+a1![]() +a0x
=bm
+a0x
=bm![]() (t)+
…+ b1
(t)+
…+ b1![]() (t)+b0
(t)+b0![]() (t).
(2.6)
(t).
(2.6)
Допустим, что при t=0 переменные уравнения (2.6.) имеют следующие значения
x(0)=![]() (0)
= ….=x(n-1)(0)=x(n)(0)=0;
(0)
= ….=x(n-1)(0)=x(n)(0)=0;
![]() (0)=
(0)=![]() ;
;
![]() =
=![]() 0
;……;
0
;……;
![]() (m-1)(0)=
(m-1)(0)=
![]() (m-1);
(m-1);
![]() (m)(0)=
(m)(0)=
![]() (m)
.
(m)
.
При заданных начальных значениях переменных изображения отдельных слагаемых уравнения (2.6) можно записать в следующем виде:
a0
x(t)←: a0X(p);
a1![]() (t)←:
a1pX(p);
(t)←:
a1pX(p);
………………….
an x (n) (t)←: anpnX(p);
b0![]() (t)←:
b0F(p);
b1
(t)←:
b0F(p);
b1![]() (t)←:
b1 (pF(p)
-
(t)←:
b1 (pF(p)
-
![]() );
);
b2![]() (t)←:
b2(
p2F(p)
- p
(t)←:
b2(
p2F(p)
- p![]() -
-
![]() );
);
……………………….. (2.7)
bm![]() (t)←:
bm (pmF(p)
– p m-1
(t)←:
bm (pmF(p)
– p m-1![]() – p m-2
– p m-2![]() -
…- p
-
…- p![]() (m-2)-
(m-2)-![]() (m-1)
).
(m-1)
).
С учетом (2.7) уравнение (2.6), записанное в операторном виде, можно представить следующим образом:
X(p) Д(р)= F(p) M(p) – MH(p) , (2.8)
где Д(р)=anpn + an-1pn-1 +…+a1p +a0 - характеристический многочлен системы, представляющий собой изображение левой части уравнения (2.6) при нулевых начальных условиях;
M(p)=bmpm+bm-1pm-1+…+b1p+b0 – многочлен представляющий собой изображение правой части уравнения (2.6) при нулевых начальных условиях;
MH(p)=![]() (bmpm-1+bm-1pm-2+…+b2p+b1)+
(bmpm-1+bm-1pm-2+…+b2p+b1)+![]() (bmpm-2+b1p3+…+b3p+
+b2)+…+
(bmpm-2+b1p3+…+b3p+
+b2)+…+![]() (m-2)(bmp+bm-1)+
(m-2)(bmp+bm-1)+
![]() (m-1)bm
- многочлен, учитывающий начальные
значения переменной f(t)
и ее производных.
(m-1)bm
- многочлен, учитывающий начальные
значения переменной f(t)
и ее производных.
На основании (2.8) изображение выходной переменной принимает вид
![]() (2.9)
(2.9)
Изображения F(p) внешних типовых воздействий представляют собой правильные рациональные дроби
![]() .
.
Тогда, уравнение (2.9) можно представить следующим образом:
![]() (2.10)
(2.10)
Используя формулы обратного преобразования Лапласа, т.е. переходя от изображения Х(р) к оригиналу х (t ) , можно записать решение уравнения (2.6).
Рассмотрим случай, когда характеристическое уравнение Д(р)=0 и уравнение F2(p)=0 не содержат нулевых и кратных корней.
Решение уравнения (2.6) с учетом (2.10) в этом случае можно представить в виде
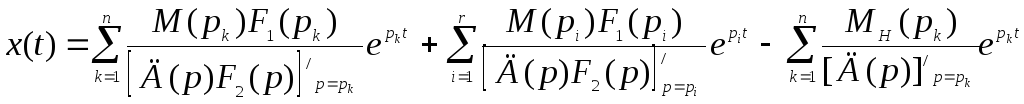 , (2.11)
, (2.11)
где pk – корни уравнения Д(р) =0 ; pi - корни уравнения F2 (p) = 0;
n
- порядок многочлена Д(р); r
- порядок многочлена F2(р);
![]()
Введем обозначения:
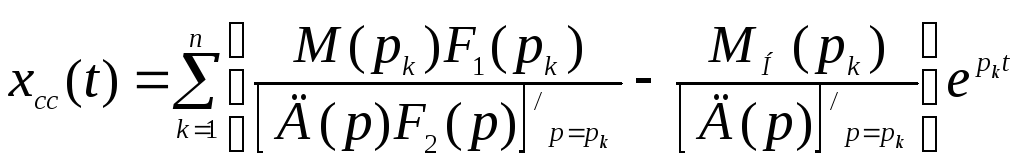 ,
(2.12)
,
(2.12)
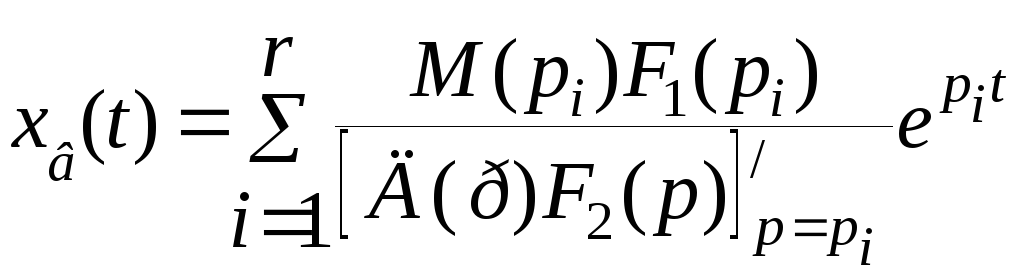 . (2.13)
. (2.13)
C учетом этого получим общее решение уравнения (2.6) в виде
х(t) = хcc(t) + хв (t) , (2.14)
где х(t) - полное движение системы, вызванное внешним воздействием f(t);
хcc(t) – собственное движение системы; хв (t) – вынужденное движение системы.
Анализ полученного решения позволяет сделать следующие выводы:
а) полное движение САУ можно условно разделить на две составляющие:
собственное движение, не зависящее от внешнего воздействия f(t), и вынужденное движение, зависящее от него;
б) если характеристическое уравнение имеет хотя бы пару комплексных корней, то собственное движение будет колебательным;
в) если характеристическое уравнение имеет хотя бы один корень с положительной вещественной частью, то амплитуда собственных колебаний будет с течением времени неограниченно увеличиваться (система неустойчивая);
г) если характеристическое уравнение имеет все корни с отрицательными вещественными частями, то собственные колебания с течением времени будут затухать, т.е. если
pk= - δk ± iωk ,
то при t→ ∞ хcc(t)→ 0, а х(t)→ хв(t) .
Таким образом, после затухания собственных колебаний полное движение системы стремится к вынужденному. Такое состояние системы называют установившемся.
Процесс перехода системы из одного установившегося состояния в другое называется переходным режимом. В переходном режиме система совершает как собственное, так и вынужденное движение. Длительность переходного режима определяется временем затухания собственных колебаний.
В
общем случае начальные условия по всем
переменным уравнения (2.6) отличны от
нуля, т.е. при
![]() :
:
![]() ,
,
![]() ,
тогда в уравнении (2.8) появляется ещё
один многочлен
,
тогда в уравнении (2.8) появляется ещё
один многочлен
![]() ,
учитывающий начальные значения переменной
,
учитывающий начальные значения переменной
![]() и её производных, т.е. начальные условия
самой системы:
и её производных, т.е. начальные условия
самой системы:
![]() ,
(2.15)
,
(2.15)
где
![]()
На основании (2.15) можно записать
![]() .
(2.16)
.
(2.16)
В соответствии с изображением (2.16) решение уравнения (2.6) будет иметь три составляющие:
![]() ,
(2.17)
,
(2.17)
где
![]() .
(2.18)
.
(2.18)
Выражение
(2.18)
характеризует свободное движение
системы, полностью определяется
корнями характеристического уравнения
и от внешнего воздействия
![]() не зависит.
не зависит.
Если
характеристическое уравнение имеет
все корни с отрицательными вещественными
частями, то свободное движение
![]() системы с течением времени затухает,
т.е. если
системы с течением времени затухает,
т.е. если
![]() ,
то
,
то
![]() и
и
![]() ,
и полное движение САУ
,
и полное движение САУ
![]() стремится к вынужденному
стремится к вынужденному
![]() .
Наступает установившийся режим. В
частном случае установившемуся режиму
САУ соответствует покой или равновесие.
.
Наступает установившийся режим. В
частном случае установившемуся режиму
САУ соответствует покой или равновесие.
