4.4. Критерий михайлова

Критерий Михайлова относится к графическим критериям. Он поз­воляет судить об устойчивости САУ любого порядка по годографу характеристического многочлена

Д(р)=а_nрⁿ+…+а₁р+а₀=а_n(р-р₁)(р-р₂)…(р-р_n), (4.16)

который при p=i можно представить в виде

. (4.17)

Каждый сомножитель (i - р_k) многочлена Д(i) можно представить на плоскости комплексного переменного в виде вектора.

0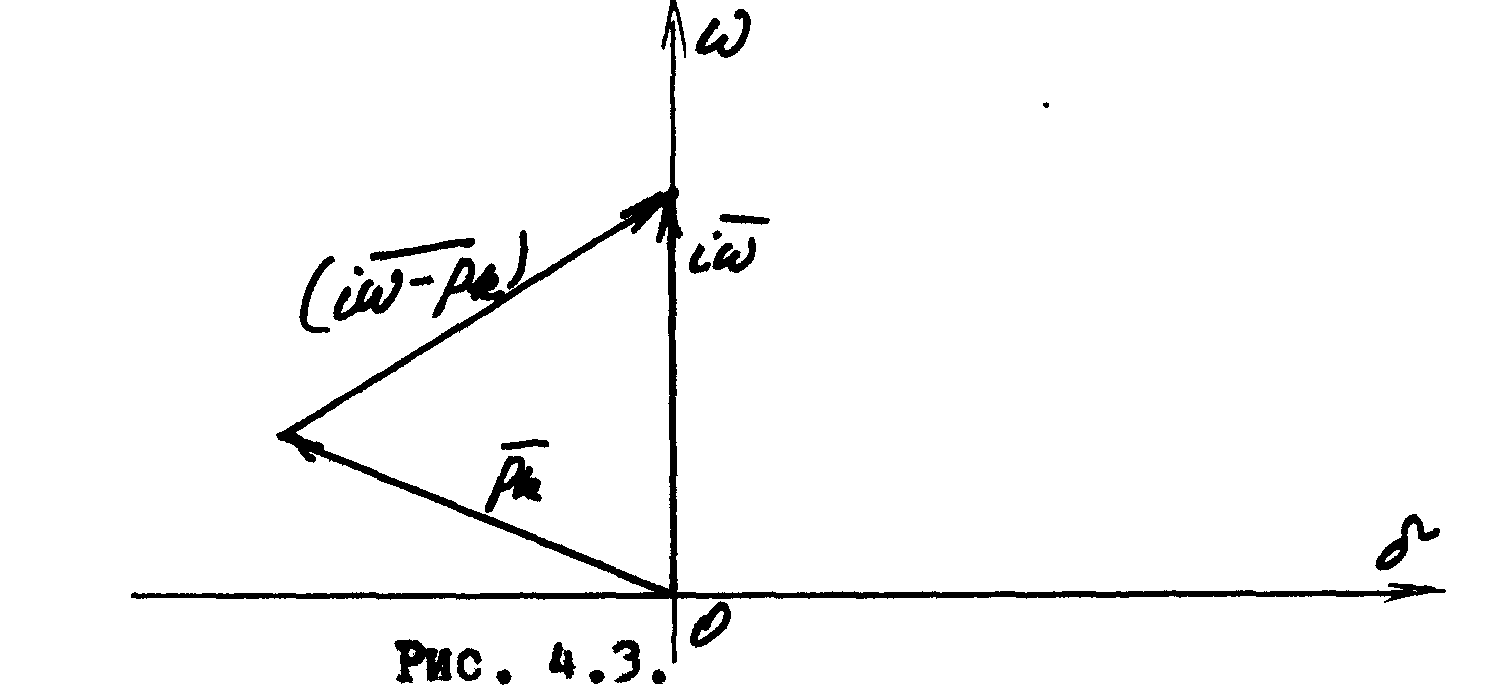

Рис. 4.3

Из рис. 4.3. видно, что если корни р_k имеет отрицательные вещественные части p_k=-_k i_k , т.е. векторы р_k расположены сле­ва от мнимой оси комплексной плоскости, то при изменении частоты  = -   каждый из векторов опишет угол против часовой стрелки (в положительном направлении), равный 180⁰. Следовательно, вектор характеристического уравнения

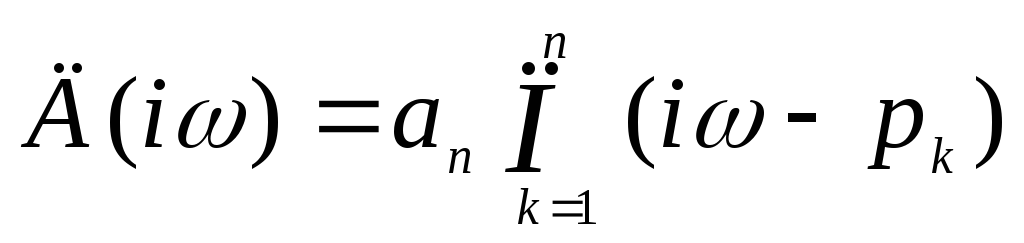
в этом случае опишет угол (180n)°. Это и есть критерий устойчивос­ти Михайлова.

Чтобы воспользоваться этим критерием, годограф характеристического уравнения, который описывает вектор Д(i), целесообразно строить в координатах V() и U():

.

Учитывая симметричность годографа относительно действительной оси (функция U() – четная), можно ограничиться построением лишь одной его половины, например, при изменении  от 0 до . Условие устойчивости в этом случае можно сформулировать следующим обра­зом: чтобы система была устойчивой, необходимо и достаточно, что­бы вектор характеристического уравнения Д(i) при изменении  от 0 до  повернулся в положительном направлении на угол (90n)° (рис. 4.4).

При =0 нечетная функция V()=0, а U()=а₀, причем а₀0. Учитывая это, критерий Михайлова можно сформулировать сле­дующим образом.

Чтобы система была устойчивой, необходимо и достаточно, чтобы годограф характеристического уравнения Д(i), начинаясь при =0 на положительной полуоси U(), при возрастании частоты от 0 до  прошел последовательно в положительном направлении n квадрантов координатной плоскости.

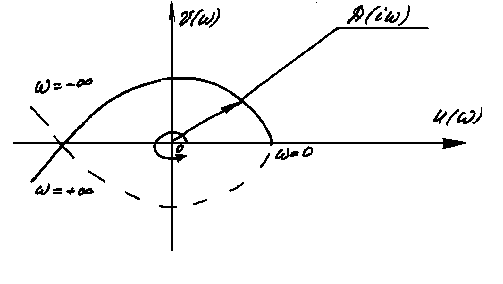
Рис. 4.4

На рис.4.5 показаны кривые Михайлова (годографы вектора Д(i)) для устойчивых систем от 1-го до 5-го порядка.

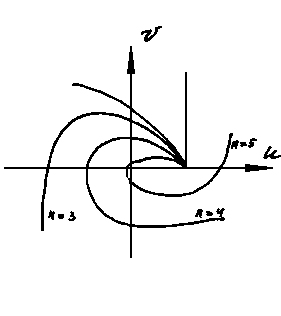
Рис. 4.5

На рис. 4.6 показаны кривые Михайлова неустойчивых систем: а) а₀<0;

б) вектор Д(i) поворачивается по часовой стрелке; в) порядок уравне­ния n=5, а кривая Михайлова находится в одном квадранте; г) нарушается последовательность прохождения квадрантов; д) система нахо­дится на границе устойчивости, т.к. кривая Михайлова проходит через начало координат; е) система неустойчива, т.к. кривая Михайлова проходит через начало координат и не последовательно пересекает квадранты.

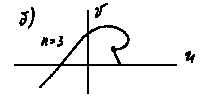
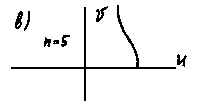
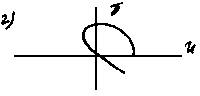
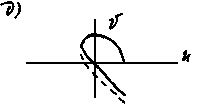
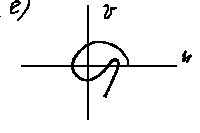
Рис. 4. 6

Рассмотрим одно из следствий критерия Михайловаусловие перемежаемости корней действительной U() и мнимой V() частей функции Д(i) .

При последовательном прохождении кривой Михайлова квадрантов координатной плоскости действительная U() и мнимая V() оси пересекаются поочередно. Отсюда следует, что действительная и мни­мая функции при возрастании  обращаются в нуль поочередно, т.е. корни их вещественны и перемежаются.

На рис. 4.7а приведен пример графиков для устойчивой системы (кривые U и V пересекают ось  поочередно); на рис. 4.7б для неустойчивой системы (очередность пересечения кривыми U и V оси  нарушена).

Условие перемежаемости корней показывает, что для суждения об устойчивости системы не обязательно точно вычерчивать всю кривую, достаточно определить ее ход лишь вблизи точек пересечения с коор­динатными осями.

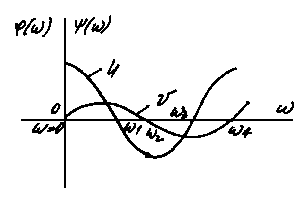
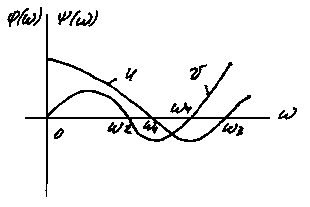
а б

Рис. 4.7