4.2. Определение устойчивости по а.М. Ляпунову

Невозмущенное движение называется устойчивым по отношению к переменным у_к , если при всяком заданном числе А, как бы мало оно ни было, можно выбрать другое положительное число λ(А) так, что для всех возмущений х_к0 , удовлетворяющее условию

возмущенное движение (4.7) будет удовлетворять неравенству

. На рис. 4.2 показано геометрическое изображение условия устойчивости в пространстве трех переменных х₁ ,х₂ , х₃ .геометрическая трактовка условия устойчивости по Ляпунову: если при возмущениях, выведших точку В₀ (х₁₀ , х₂₀ , х₃₀) за границу сферы λ, возмущенное движение будет таково, что точка не выйдет за границу сферы А, то оно устойчиво.

Если с течением времени возмущенное движение стремится к началу координат, то система асимптотически устойчива. При том

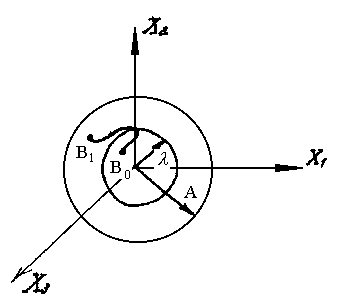
Рис. 4.2

Определение устойчивости по Ляпунову относится к движению, а не к системе. САУ может быть устойчива по отношение к одному движению и неустойчива по отношению к другому. Например, система регулирования скорости вала машины, устойчивая к изменению скорости, будет неустойчивой к изменению угла поворота. Но для краткости в дальнейшем будем говорить об устойчивых и неустойчивых САУ. Под устойчивостью САУ по существу подразумевается устойчивость процесса регулирования, т.е. устойчивость равновесия, или в более общем случае устойчивость частного решения дифференциального уравнения.

На практике при исследовании устойчивости реальных САУ часто пользуются линейными уравнениями, полученными в результате линеаризации, т.е. в результате отбрасывания членов, содержащих вторые и высшие степени, а также произведения отклонений переменных и их производных. В связи с этим возникают вопросы о возможности определения устойчивости реальных систем по их линеаризованным уравнениям.

Приведем интерпретацию теорем Ляпунова для линейных систем.

1. Линейная система устойчива, причем асимптотически, если все корни ее характеристического уравнения имеет отрицательные ве­щественные части.

2. Линейная система неустойчива, если среди корней ее характеристического уравнения есть хотя бы один корень с положительной вещественной частью.

3. Линейная система не асимптотически устойчива, если среди корней ее характеристического уравнения один нулевой, а у осталь­ных отрицательные вещественные части.

С точки зрения дифференциальных уравнений в устойчивой линей­ной системе собственные колебания с течением времени затухают и полное движение стремится к вынужденному, т.е. решение дифферен­циального уравнения, определяющее возмущенное уравнение системы, стремится к частному решению. Это будет только в том случае, если корни р_k характеристического уравнения Д(р)= 0 будут иметь отрицательные вещественные части, т.е.

р_k= – d_k ± iw_k . (4.8)

Наличие одного нулевого корня в характеристическом уравнении приводит к тому, что с течением времени собственное движение стремится не к нулю, а к некоторой постоянной величине, зависящей от начальных условий.

Математическая формулировка условий, которым должны удовлетво­рять коэффициенты характеристического уравнения устойчивой системы, или другие формы выражения условий устойчивости, называется критери­ями устойчивости.

На практике применяет в основном алгебраические и частотные критерии устойчивости, в том числе критерии Рауса, Гурвица, Вышнеградского, Михайлова, Найквиста и др.

Все эти критерии позволяют исследовать устойчивость линейных замкнутых систем регулирования, не прибегая к решению уравнений и к определению корней характеристического уравнения.