
- •В.И. Родионов
- •Теория автоматического управления Конспект лекций
- •Часть 1
- •Введение ……………………………………………………….……………….…5 в.1. Значение автоматического управления и задачи курса………….………5
- •Лекция 2
- •Основные понятия и определения тау
- •Функциональные элементы сау
- •Классификация систем автоматического
- •1.3. Примеры систем автоматического управления
- •2. Математическое описание сау
- •Вынужденное движение и собственные колебания системы. Переходный и установившийся режимы
- •2.3. Передаточные функции
- •2. Типовые звенья сау.
- •2.4. Переходная характеристика и весовая функция
- •Типовые звенья систем автоматического
- •2.6. Неустойчивые и неминимально–фазовые звенья
- •1. Структурные схемы сау.
- •3. Передаточные функции замкнутой и разомкнутой системы.
- •2.7. Структурные схемы сау
- •2.8. Составление и преобразование структурных схем сау
- •2.9. Передаточные функции замкнутой и разомкнутой
- •Установившиеся режимы
- •Точность сау в установившемся режиме.
- •Установившиеся ошибки следящих систем.
- •3.1. Точность сау в установившемся режиме
- •3.2. Установившиеся ошибки следящих систем
- •Частотные характеристики сау.
- •Частотные характеристики сау
- •Логарифмические амплитуднные и фазовые
- •3.5. Частотные характеристики типовых звеньев
- •3.6. Особенности частотных характеристик устойчивых
- •4. Устойчивость систем автоматического управления
- •Определение устойчивости по Ляпунову.
- •Критерий устойчивости Гурвица.
- •4.1. Общие понятия об устойчивости заданного режима
- •4.2. Определение устойчивости по а.М. Ляпунову
- •3. Критерий устойчивости гурвица
- •Таким образом, кроме положительности коэффициентов а30; а20; а10; а00
- •4.4. Критерий михайлова
- •4.5. Критерий найквиста
- •4.6. Суждение об устойчивости по лафчх
- •4.7. Выделение областей устойчивости
- •Суждение об устойчивости системы по ее линейной модели.
- •Суждение об устойчивости системы
- •5. Качество сау
- •5.1. Основные показатели качества
- •5.2. Методы построения переходных процессов
- •Преобразования Фурье имеют вид:
- •5.2.1 . Частотный метод анализа качества сау,
- •Приближенный метод построения кривой переходного процесса с помощью трапециидальных частотных
- •Лекция 14
- •5.3. Построение вещественной частотной характеристики замкнутой системы по частотным характеристикам
- •План лекции:
- •5.5. Косвенные оценки качества, связанные с распределением нулей и полюсов передаточной функции
- •5.7. Интегральные оценки качества
- •5.8. Косвенные оценки качества, связанные с видом
- •5.8.1. Анализ качества по ачх замкнутой системы
- •5.8.2. Оценка качества сау по логарифмическим частотным
- •Приближенная оценка вида переходного процесса
- •6. Динамический синтез сау
- •Методы коррекции динамических свойств сау.
- •6.1. Общие понятия синтеза сау
- •6.2. Этапы синтеза сау
- •6.3. Требования, предъявляемые к динамическим
- •Методы коррекции динамических свойств сау.
- •6.5. Методы коррекции динамических свойств системы,
- •6.5. Динамический синтез сау, основанный
- •Синтез последовательного корректирующего устройства.
- •Синтез параллельного корректирующего устройства.
- •6.6. Синтез последовательного корректирующего устройства
- •6.7. Синтез параллельного корректирующего устройства
- •7. Методы синтеза, основанные на теории
- •7.1. Уравнения системы в пространстве состояний
- •7.2. Коррекция системы в пространстве состояний
- •7.3. Прямой корневой метод синтеза
- •7.4. Прямой корневой метод синтеза сау
- •7.5. Прямой метод синтеза корректирующей обратной
- •Лекция 22
- •8.2. Основные вероятностные характеристики
- •8.2.1. Функция распределения и плотность вероятности
- •8.2.2. Математическое ожидание, дисперсия
- •8.3. Стационарные случайные процессы.
- •8.3.1. Стационарные случайные процессы
- •8.3.2. Эргодические случайные процессы
- •Спектральная плотность стационарного
- •8.5. Свойства корреляционных функций и спектральных плотностей стационарных эргодических
- •8.6. Статистические характеристики случайных
- •8.6.1. Белый шум
- •8.6.2. Корреляционная функция и спектральная плотность скорости изменения азимута
- •8.6.3. Спектральная плотность задающего воздействия системы наведения ракеты на цель
- •8.7. Экспериментальное определение корреляционных функций, спектральных плотностей и дисперсий
- •8.8. Прохождение случайных воздействий
- •8.8.1. Интегральное Уравнение связи
- •8.8.2. Спектральное уравнение связи
- •8.8.3. Определение динамических характеристик сау
- •8.9. Методы определения ошибок линейных сау,
- •8.9.1. Эквивалентное представление стационарного
- •8.9.2. Расчет флуктуационных ошибок и ошибок
- •8.9.3. Графоаналитический метод расчета
- •8.9.4. Оценка флуктуационных ошибок, обусловленных
- •8.9.5. Расчет дисперсии помехи с помощью
- •8.9.6. Вычисление среднеквадратической ошибки
4.5. Критерий найквиста
Частотный
критерий Найквиста позволяет судить
об устойчивости замкнутой системы по
амплитудно-фазовой частотной характеристике
разомкнутой системы W(i),
которая строится в координатах
действительной
![]() и мнимой
и мнимой
![]() частей АФЧХ (рис.4.8).
частей АФЧХ (рис.4.8).
Чтобы определить условие устойчивости по критерию Найквиста, необходимо найти связь между функциями W(i) и Д(i). Для этого рассмотрим функцию
![]() ,
(4.18)
,
(4.18)
представляющую собой знаменатель передаточных функций замкнутой системы.
Передаточную функцию разомкнутой системы W(р) можно представить в виде отношения двух многочленов
![]() ,
(4.19)
,
(4.19)
где Т(р) часто называют характеристическим многочленом разомкнутой системы. С учетом (4.19) выражение (4.18) можно представить в следующем виде:
![]() ,
(4.20)
,
(4.20)
где Д(р)=Т(р)+R(р) - характеристический многочлен замкнутой системы, причем порядок многочлена Д(р) определяется порядком многочлена Т(р) и равен n.
Заменяя р на i, будем иметь
![]() ,
(4.21)
,
(4.21)
![]() . (4.22)
. (4.22)
Анализ (4.21) показывает, что вектор W*(i) смещен на единицу по отношению к вектору W (i). Причем, они описывают один и гот же годограф – АФЧХ разомкнутой системы W(i) (рис. 4.9). Эго позволяет условие устойчивости связать как с поведением вектора W(i) , так и вектора W*(i).
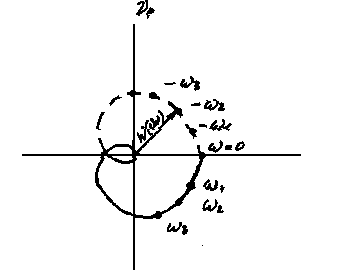
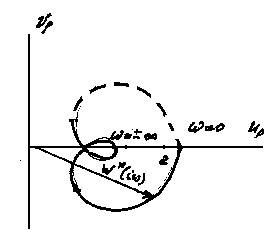
Рис. 4.8 Рис. 4.9
На основании (4.22) можно записать
arg W*(i)= arg Д (i)-arg Т (i). (4.23)
При изменении частоты от - до для обеспечения устойчивости системы в соответствии с критерием Михайлова
arg Д (i)=180оn . (4.24)
Следует иметь в виду, что устойчивая замкнутая система может оказаться неустойчивой в разомкнутом состоянии, поэтому характеристическое уравнение разомкнутой системы Т(р)=0 может иметь корни с положительными действительными частями (правые корни). Положим, что уравнение Т (р)=0 имеет r правых корней и (n-r) левых, тогда в соответствии c рис. 4.4. вектор Т (i) при изменении частоты от - до опишет угол в положительном направлении 180о(n-r) и в отрицательном -180or, т.е.
arg Т (i)=180о(n-r)-180or=180оn-360or . (4.25)
С учетом (4.24) и (4.25) уравнение (4.23) принимает вид
arg W*(i)=180оn-180оn+360or=360or. (4.26)
Учитывая симметричность АФЧХ относительно действительной оси (Up() –функция четная), условие (4.26) можно переписать в виде
![]() .
(4.27)
.
(4.27)
Отсюда вытекает формулировка критерия Найквиста.
Для того, чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы при изменении частоты от 0 до вектор W*(i) повернулся в положительном направлении на угол 1800r, где r - число правых корней характеристического многочлена разомкнутой системы, т.е. чтобы АФЧХ разомкнутой системы W(i) охватила точку (-1, 0i) в положительном направлении r/2 раз.
Если разомкнутая система устойчивая, то r=0 и условие (4.27) принимает вид
![]() ,
(4.28)
,
(4.28)
т.е. суммарный угол поворота вектора W*(i) вокруг начала координат должен равняться нулю. Это будет в том случае, когда АФЧХ не охватывает точку (-1, 0i) т.е. пересекает действительную ось в диапазоне (0 -1).
Условие устойчивости в этом случае можно сформулировать следующим образом. Для того чтобы замкнутая система была устойчива в случае устойчивой разомкнутой системы, необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика разомкнутой системы не охватывала точку (-1, 0i), т.е. пересекала бы действительную ось правее этой точки (рис. 4.10а).
Если АФЧХ пересечет действительную ось в точке (-1, 0i), то соответствующая ей система будет находиться на границе устойчивости (рис.4.10в). Случай показанный на рис. 4.10г, соответствует неустойчивой системе.
Для систем высокого порядка могут возникнуть затруднения при определении угла, на который поворачивается вектор W*(i). В этом случае для суждения об устойчивости, можно рекомендовать следующую интерпретацию критерия Найквиста, предложенную Я.З. Цыпкиным.
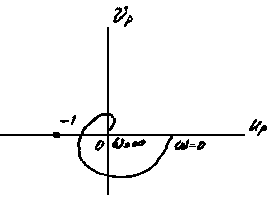 а
а
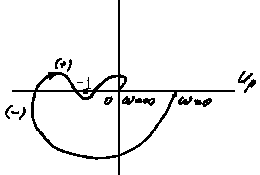 б
б
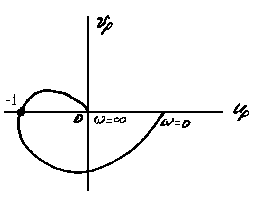 в
в 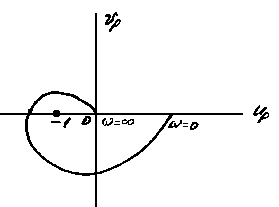 г
г
Рис. 4. 10
Система будет устойчивой, если разность между числом положительных и отрицательных переходов АФЧХ W(i) через отрезок действительной оси (- -1) при изменении от 0 до будет равна r, где r- число правых корней характеристического уравнения разомкнутой системы.
При этом переход АФЧХ через действительную ось сверху вниз считается положительным, снизу вверх - отрицательным.
Разность положительных и отрицательных переходов АФЧХ действительной оси Up в диапазоне (- -1) (рис.4.10б) равна нулю, следовательно, замкнутая система, соответствующая этому случаю, будет устойчива.
Для астатических систем характеристический многочлен разомкнутой системы Т(р) имеет нулевые корни Т (р)=рТ*(р), т.е. передаточная функция разомкнутой системы в этом случае принимает вид
![]() ,
(4.29)
,
(4.29)
где - порядок астатизма.
Заменяя в выражении (4.29) р на i , получим
![]() (4.30)
(4.30)
Анализ (4.30) показывает, что при =0 АФЧХ разомкнутой системы W(i) терпит разрыв. Чтобы избежать неопределенности в точке разрыва при построении АФЧХ разомкнутой системы, условились обходить начало координат в плоскости комплексного переменного справа по дуге бесконечно малого радиуса (рис.4.11).
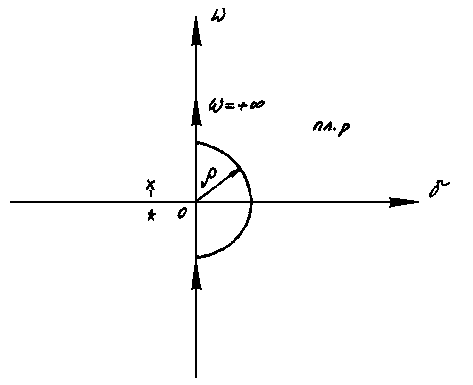
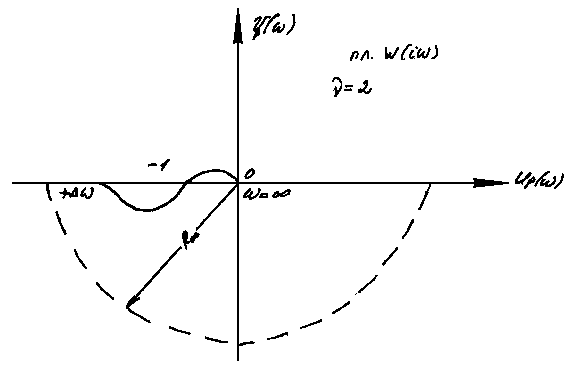
Рис 4.11 Рис. 4.12
Из выражения (4.30) следует, что при изменении частоты в окрестности нуля (=- ) АФЧХ разомкнутой астатической системы можно представить в виде дуги, которую описывает бесконечно большой радиус R. При этом в диапазоне = + АФЧХ разомкнутой астатической системы строится обычным методом, а затем дополняется дугой, которую должен описать радиус, вращаясь по часовой стрелке на угол (90ν)° .
Определение устойчивости по АФЧХ разомкнутой астатической системы, дополненной дугой бесконечно большого радиуса, ведется точно так же, как и для статических систем.
На рис. 4.12. показана АФЧХ устойчивой системы при наличии астатизма второго порядка.
Рассмотренные особенности применения критерия Найквиста для астатических систем можно распространить и на случай, когда характеристическое уравнение разомкнутой системы имеет чисто мнимые корни i1. В отличие от предыдущего случая наличие в уравнении Т(р)=0 мнимых корней связано с разрывом W(i) при = i1.
ЛЕКЦИЯ 11
План лекции:
1. Определение устойчивости по ЛАФЧХ.
2. Д - разбиение в плоскости комплексного параметра.
-
Рекомендуемая литература [1, 3, 8].
