План лекции:

1. Оценки качества, связанные с распределением нулей и полюсов

передаточной функции.

2. Степень устойчивости и колебательность САУ.

3. Диаграмма качества.

4. Рекомендуемая литература [7, 1, 6 ].

5.5. Косвенные оценки качества, связанные с распределением нулей и полюсов передаточной функции

Косвенные оценки качества позволяют определить основные показатели качества без построения кривой переходного процесса, т.е. косвенными методами. Являясь приближенными оценками, они позволяют существенно сократить время исследования САУ.

В общем случае дифференциальное уравнение линейной САУ имеет вид

.

Изображение Х (р) можно записать в виде

,

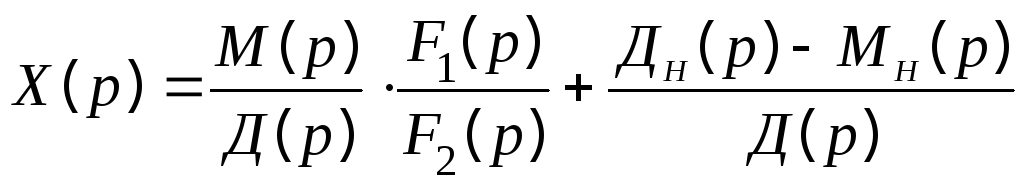или

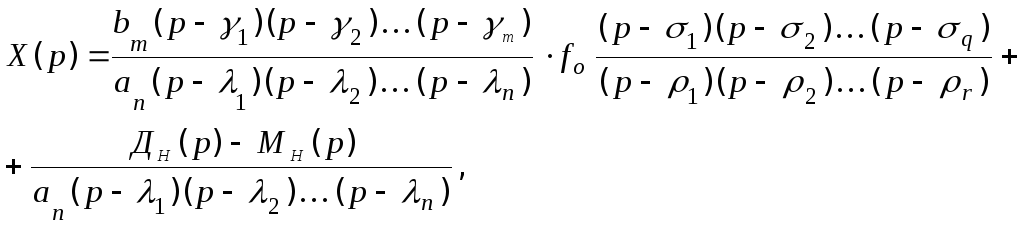(5.28)

где 1,2,...,n – корни характеристического уравнения Д(р) называются полюсами передаточной функции;

1,2,...,m – корни уравнения М(р) - нули передаточной функции;

1,2,...,q – корни уравнения F1(p)=0 - нули воздействия;

1,2,...,r – корни уравнения F2(p)=0 - полюсы воздействия.

Выражение (5.28) показывает, что в общем случае движение системы в переходном режиме зависит от нулей и полюсов передаточной функции, нулей и полюсов воздействия, начальных условий по всем переменным.

Переходя к оригиналу, в соответствии со второй теоремой разложения будем иметь

x(t)=xc(t)+xв(t),

где xc(t)=xcc(t)+xcд(t):

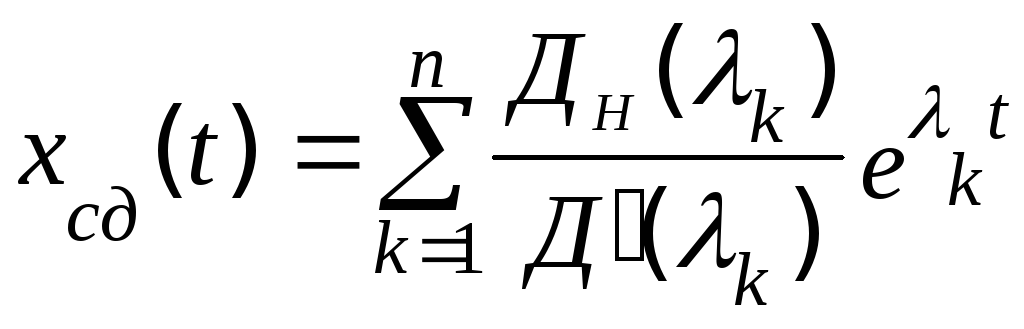; (5.29)

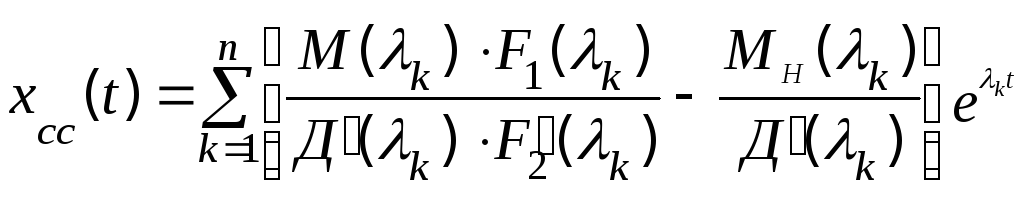; (5.30)

. (5.31)

Анализ выражений позволяет сделать следующие выводы:

1. Свободное движение хсд(t), вызванное начальным состоянием системы, не зависит от нулей и полюсов воздействия и полностью определяется корнями характеристического уравнения и начальными условиями переменной х(t) и ее производных. Чем дальше расположены полюсы передаточной функции от мнимой оси на плоскости комплексного переменного р, тем быстрее затухают свободные колебания.

2. Составляющая собственного движения хсс(t) зависит oт относительного расположения нулей и полюсов передаточной функции

М(к)= bm(к-1)(к-2)(к-m), (5.32)

от относительного расположения полюсов передаточной функции и нулей воздействия

(5.33)

и от относительного расположения полюсов передаточной функции и полюсов воздействия.

.

Выражения (5.32) и (5.33) позволяют так выбрать соотношение нулей и полюсов передаточной функции и воздействия, чтобы амплитуда собственных колебаний была бы минимальна.

Так, чем ближе нули воздействия к полюсам передаточной функции и чем дальше расположены полюсы воздействия от полюсов передаточной функции, тем меньше величина первого слагаемого в выражении (5.30).

Так же целенаправленно можно уменьшать и второе слагаемое в этом выражении.

3. Вынужденное движение хв(t) зависит от относительного расположения полюсов воздействия и нулей передаточной функции

М(_)= bm (-1)(-2)(-m) , (5.34)

от взаимного расположения нулей и полюсов воздействия

F1() = f₀ (-1)(-2)(-q)

и от относительного расположения полюсов воздействия и полюсов передаточной функции

Д() = an (-1)(-2)(-n).

Если f(t) представляет собой возмущающее воздействие, то вынужденные колебания, вызванные этим воздействием, необходимо исключить или хотя бы уменьшить амплитуду этих колебаний. Для этого нули передаточной функции и нули воздействия должны располагаться на плоскости р как можно ближе к полюсам воздействия, а полюсы передаточной функции должны находиться как можно дальше от полюсов воздействия.

Если f(t) представляет собой управляющее воздействие, то система должна воспроизводить его, как можно точнее, т.е.

xв(t) f(t). В этом случае при выборе структуры и параметров САУ необходимо стремиться к тому, чтобы М()Д() Решение поставленной задачи в общем виде для систем высокого порядка связано с большими трудностями, поэтому на практике ограничиваются рассмотрением частных случаев.

Полагают, например, что начальные условия по всем переменным

нулевые, т.е. ДН(р)=0 и МН(р), внешнее воздействие принимается в виде f(t)=c1(t), т.е. , считают, что многочлен М(р) не зависит от р. В этом случае уравнение (5.28) принимает вид

и движение системы в переходном режиме полностью определяется полюсами передаточной функции, т.е. корнями уравнения

Д(р) = 0.

Таким образом, о качестве регулирования можно судить по расположению полюсов передаточной функции λ₁ , λ₂,…, λ_n на плоскости комплексного переменного р=  i .

О характере расположения полюсов передаточной функции на плоскости р судят, по координатам трапеции (рис.5.7), внутри которой расположены все корни k, а ближайшие к мнимой оси и наиболее удаленные от оси корни лежат на сторонах трапеции.

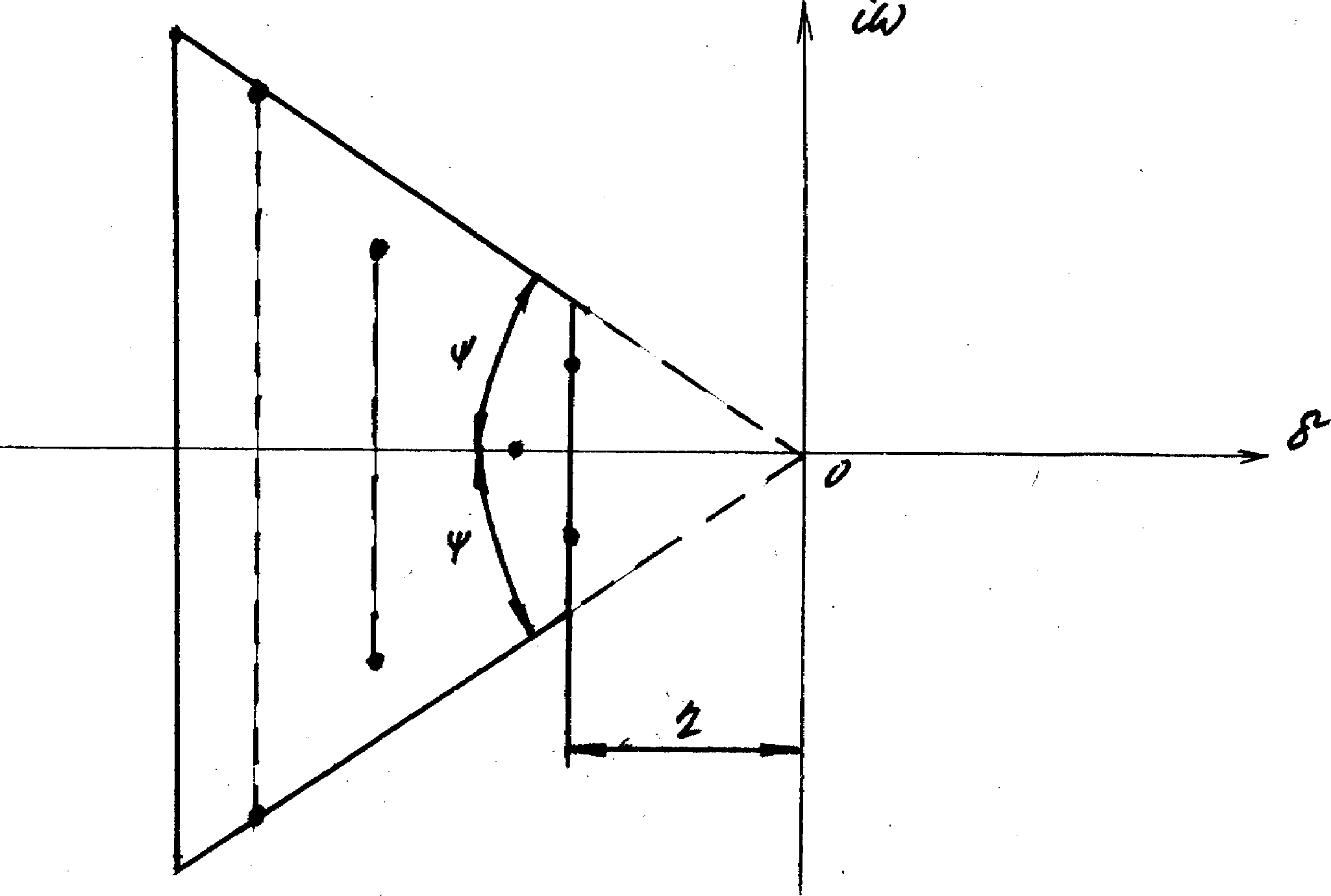
Рис.5.7

На рис.5.7 приняты следующие обозначения:

 - абсолютная величина действительной части полюса, ближайшего к мнимой оси;

 - наибольший угол, внутри и на границе которого расположены все полюсы передаточной функции.

Величина  называется степенью устойчивости САУ. Если ближайший к мнимой оси корень действительный, то степень устойчивости называется апериодической, если ближайший к мнимой оси корень комплексный, то степень устойчивости называется колебательной.

Величина называется колебательностью системы. Если все корни действительные, то колебательность равна нулю, если имеется чисто мнимый корень, то колебательность равна бесконечности, т.е. в линейной системе воз­никают незатухающие колебания,

Для определения степени устойчивости  мнимая ось на плоскости р переносится влево на величину . Тогда характеристическое уравнение

(5.37)

записанное для новой переменной

z = p + , (5.38)

принимает следующий вид:

(5.39)

где Ak - постоянные коэффициенты.

Уравнение (5.39) называется смещенным характеристическим уравнением. Оно имеет, по крайней мере, один мнимый корень. При этом система находится на границе устойчивости, следовательно, старший определитель Гурвица, составленный по этому уравнению, должен быть равен нулю:

∆n = ∆_n-1∙A0 = 0. (5.40)

Равенство (5.40) возможно в двух случаях.

1. ∆_n-1 = 0; A0>0 и все остальные диагональные миноры определителя ∆n положительны.

В этом случае степень устойчивости – колебательная.

2. А0 = 0; ∆n-1 > 0 и все остальные условия устойчивости выполняются.

В этом случае уравнение (5.39) имеет один нулевой корень, следовательно, уравнение (5.37) имеет ближайший к мнимой оси корень действительный, т.е. степень устойчивости в этом случае будет апериодической.

В качестве примера рассмотрим диаграмму Вышнеградского для уравнений третьего порядка

Приведя его к нормированному виду, получим

, (5.41)

где ;

Введем новую переменную z = U + η.

Смещенное характеристическое уравнение принимает вид

. (5.42)

Коэффициенты А0, А1 и А2 определяются по формулам:

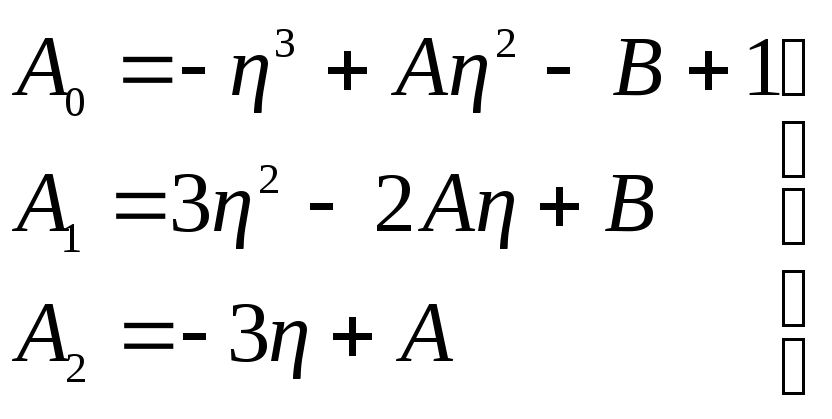
Определитель Гурвица, составленный по уравнению (5.42), имеет вид

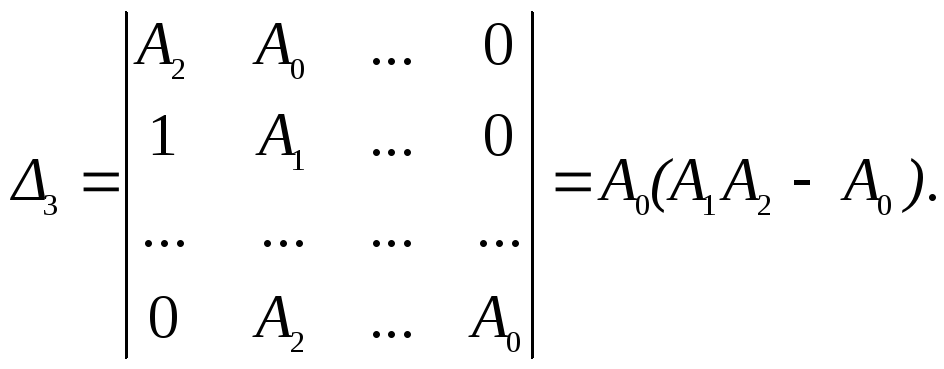
В случае апериодической устойчивости

А0 = 0; А1>0; А2>0,

т.е. 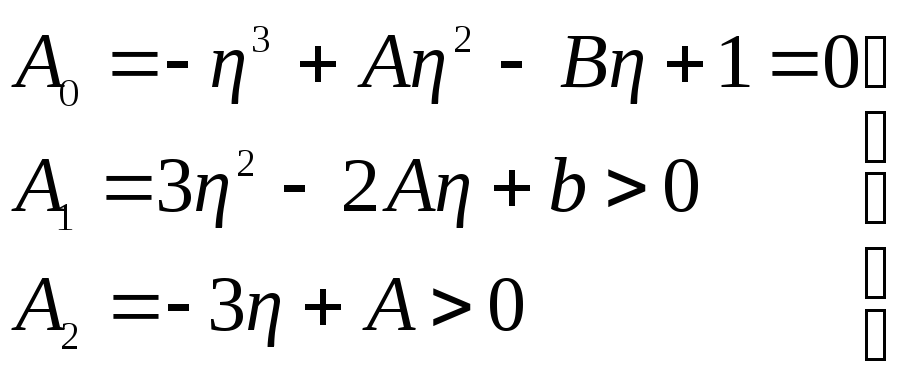. (5.43)

Система (5.43) представляет собой параметрическое уравнение прямой. Задаваясь различными значениями η на плоскости А,В можно построить линии равной степени устойчивости. Эти линии наносятся в тех областях, для которых справедливы неравенства системы (5.43). Для определения границ этих областей можно воспользоваться следующими равенствами:

(5.44)

Система (5.44) представляет собой уравнения граничной кри­вой в неявном виде. На основании (5.44) запишем уравнения граничной кривой в параметрической форме

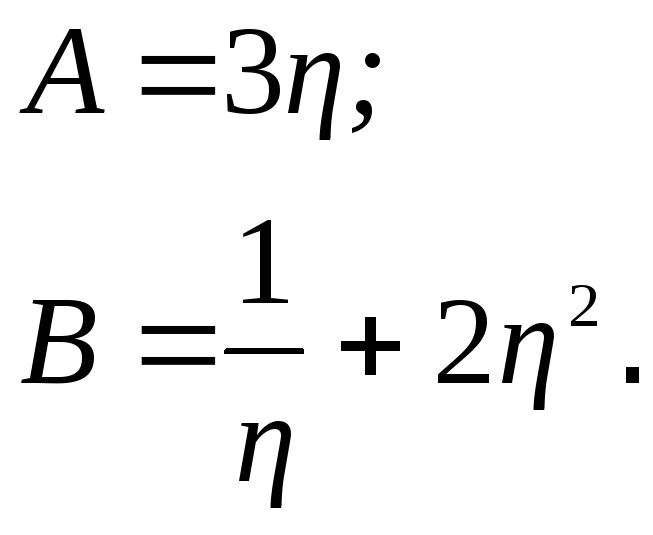
(5.45)

Уравнение (5.45) справедливо, если

. (5.46)

Граничная кривая p , построенная по уравнениям (5.45) при 0 < η < 1, показана на рис. 5.8. Для построения второй граничной кривой воспользуемся следу­ющими уравнениями системы (5.43)

(5.47)

(5.48)

Уравнения (5.47) граничной кривой в параметрической форме принимает вид

(5.49)

При А2 = -3η + А >0 , т.е. при η < 1 граничная кривая, построенная на плоскости А,В по уравнениям (5.49), имеет вид Q , показанный на рис. 5.8.

Граничные кривые Р и Q полностью определяют область апериодической степени устойчивости. Вышнеградский доказал, что при η  1 можно построить кривую R, которая делит область апериодической степени устойчивости на две области: область между кривыми R и Q соответствует монотонному пе­реходному процессу, все корни уравнения (5.41), соответствующие этой области, – действительные.

Область между кривыми Р и R соответствует монотон­ному переходному процессу, в котором присутствует колебательная составляющая, вызванная комплексным корнем, наиболее удаленным от мнимой оси.

В случае колебательной степени устойчивости

2 = 0; А0 >0; A1 >0,

т.е. (5.50)

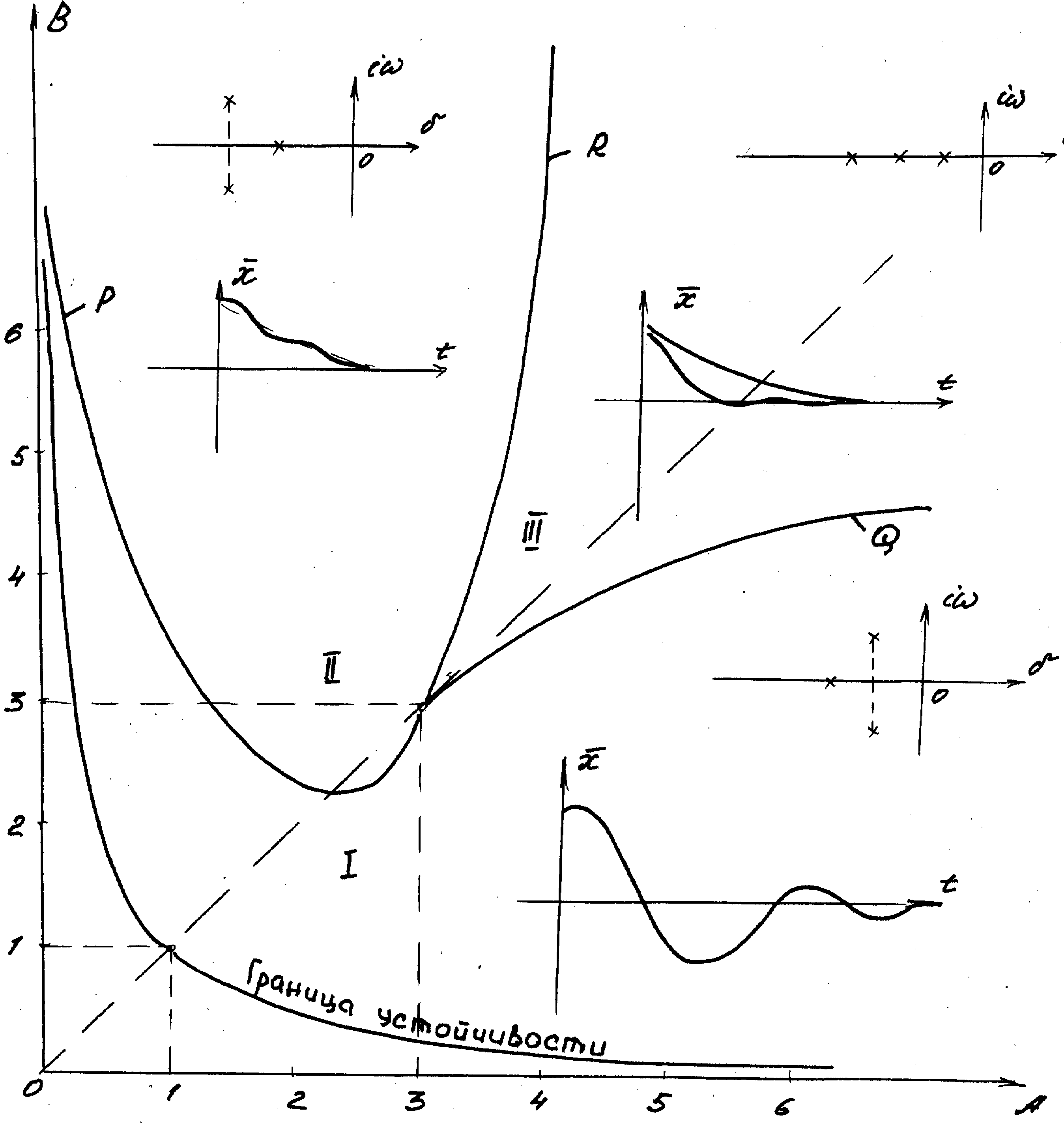
Рис. 5.8

Уравнение (5.50) в сочетании с неравенствами позво­ляет построить линии равных значений в области колебательной сте­пени устойчивости. Нетрудно показать, что граничными кривыми этой области (рис.5.8) являются гиперболы.

Наибольшая степень устойчивости =1 имеет место в точке с координатами А=3 и В=3, следовательно, эта течка соответствует наилучшим значениям параметров с точки зрения величи­ны степени устойчивости и затухания переходного процесса.

При определении колебательности  мнимая ось поворачивается вокруг начала координат против часовой стрелки на угол (/2-). Диаграммы Вышнеградcкого строятся с нанесенными линиями рав­ного затухания  = соnst или линиями равной колебательности  = соnst. Колебательность и затухание связаны между собой следующими формулами:

; .

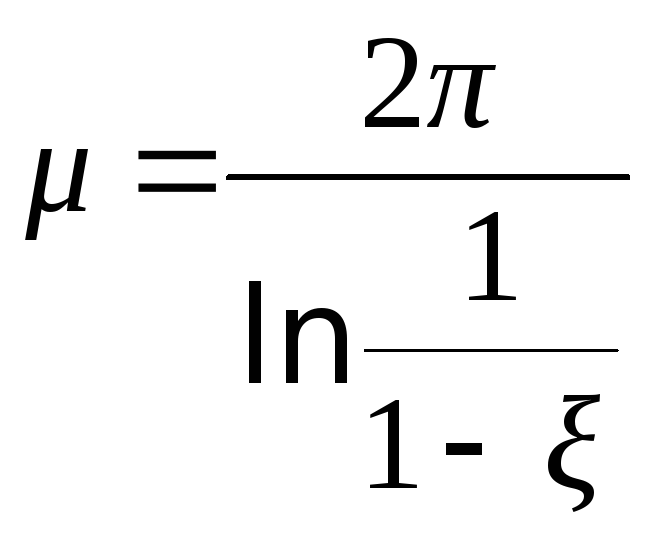Покажем это. Если , то для t = t1 имеем

.

Через период T = 2/ :

Показатель затухания

.

Обычно в CAУ допускается затухание за один период не менее, чем 90 – 98%. Так, например, если ξ = 98%, то допустимая колебательность составит

.

Соответственно при ξ = 90% получим  = 2,73. По известным значениям  и  можно определить другие показателя качества, например, время переходного процесса

.

Откуда при ∆= 5% получим

Лекция 16

План лекции:

1. Интегральные оценки качества САУ.

2. Оценки качества САУ по виду частотных характеристик.

3. Рекомендуемая литература [1, 2, 6].