8.6. Статистические характеристики случайных

типовых процессов

Лекция 25

План лекции:

1.Статистические характеристики «белого шума».

2. Корреляционная функция и спектральная плотность скорости

изменения азимута маневрирующей цели.

3. Спектральная плотность задающего воздействия системы наведения ракеты на цель.

4. Рекомендуемая литература [9].

Рассмотрим некоторые случайные стационарные процессы, встречающиеся при исследовании САУ.

8.6.1. Белый шум

Случайный процесс, характеризуемый спектральной плотностью во всем диапазоне частот, т. е. имеющий равномерный на всех частотах спектр, называют белым шумом . В соответствии с (8.29) корреляционная функция белого шума имеет вид , т. е. является -функцией, что указывает на отсутствие корреляционной связи между любыми сколь угодно близкими друг к другу значениями случайного процесса. Процесс такого типа является математической идеализацией реального процесса.

Дисперсия этого процесса будет бесконечно большой , а значит и мощность, необходимая для создания такого процесса, также бесконечна. Однако в тех случаях, когда спектр случайного воздействия значительно превосходит полосу пропускания частот исследуемой системы и равномерен в пределах этой полосы, реальный спектр можно заменить белым шумом. Случаи, когда реальный спектр помехи можно аппроксимировать белым шумом, встречаются в практике достаточно часто. Примером процесса типа белого шума является тепловой шум сопротивления.

8.6.2. Корреляционная функция и спектральная плотность скорости изменения азимута

маневрирующей цели

Рассмотрим корреляционную функцию и спектральную плотность случайного процесса, имеющего место на входе системы автоматического сопровождения цели. Подобный сигнал представлен на рис. 8.6, а. Он характеризует изменение углового перемещения самолета — угловой координаты цели относительно системы сопровождения радиолокатора. На рис. 8.6, а видно, что кривая не является стационарным случайным процессом. Однако поведение цели можно представить так, будто угловая скорость движения цели в течение некоторого интервала времени остается постоянной, затем скачком меняется и на сле­дующем интервале также остается постоянной (рис. 8.6, б).

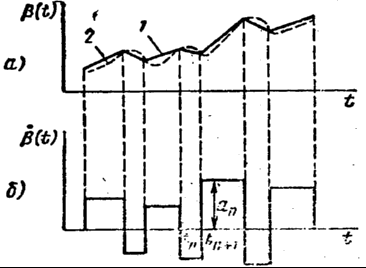
Рис. 8.6. Изменения угловой координаты маневрирующей цели (а)

и ее производной (б)

При этом моменты скачков и значения скоростей — случайные величины. Такая картина соответствует движению цели в направлении на радиолокатор и идеализированному маневру ее в горизонтальной плоскости (мгновенное изменение курса).

Значения функции в любых двух интервалах взаимно независимы, но имеют одинаковые функции распределения вероятности.

Случайный стационарный процесс в данном случае может быть определен так:

при (8.42)

где а_n— независимые случайные переменные, имеющие одинаковое распределение вероятности.

Для определения корреляционной функции необходимо найти среднее значение произведения:

. (8.43)

Возможны два случая.

Если моменты времени и таковы, что величины и находятся в одном интервале , то среднее значение произведения угловых скоростей равно среднему квадрату угловой скорости или дисперсии:

. (8.44)

Если и таковы, что эти величины лежат в разных интервалах, то искомое произведение скоростей равно нулю:

, (8.45)

так как произведения с положительными и отрицательными знаками равновероятны. В результате корреляционная функция

, (8.46)

где P₁ - вероятность нахождения значений скорости и в одном интервале;

P₂ = 1 - P₁ — вероятность нахождения их в разных интервалах.

Обозначим через среднее число перемен скорости за 1 с. Тогда будет средним значением интервала времени, в течение которого угловая скорость сохраняет постоянную величину. Будем полагать, что вероятность появления перемены скорости в течение малого промежутка времени пропорциональна этому промежутку и равна . Вероятность отсутствия перемены скорости для этого же промежутка . Для интервала времени вероятность отсутствия перемены скорости, т. е. вероятность нахождения моментов времени и в одном интервале постоянной скорости, равна произведению вероятностей отсутствий перемены скорости в каждом элементарном промежутке , так как эти события независимы.

Следовательно, для конечного промежутка

, (8.47)

где - среднее количество промежутков .

Переходя к пределу при , получим

. (8.48)

Функцию распределения (8.48) называют распределением Пуассона. Таким образом, искомая корреляционная функция

, (1.49)

т. е. оказывается экспоненциально затухающей.

Спектральная плотность для рассматриваемого процесса

, (8.50)

где —средний квадрат угловой скорости;

—средняя длина промежутков времени, в течение которых скорость остается постоянной. Величину находят экспериментально на основании изучения распределения угловых скоростей слежения за самолетом, а - путем определения средней продолжительности прямолинейного движения маневрирующего самолета.