8.3. Стационарные случайные процессы.

Эргодическая гипотеза

Лекция 23

План лекции:

1. Стационарные случайные процессы.

2. Эргодические случайные процессы.

3. Рекомендуемая литература [9].

8.3.1. Стационарные случайные процессы

Различные случайные процессы по степе­ни зависимости их статистических характеристик от времени делят на стационарные и нестационарные.

Наиболее просто осуществляется анализ случайных процессов, статистические характеристики которых не зависят от текущего времени. Такие процессы называют стационарными.

Реальные физические процессы в большей или меньшей степени приближаются к стационарным процессам. Многие из них, например тепловые шумы, можно с большой точностью считать стационарными. К стационарным относятся также колебания самолета относительно установившегося горизонтального полета, шумы в радиоэлектронной аппаратуре, качка корабля и др.

Ко многим нестационарным процессам применяют результаты, полученные при исследовании стационарных процессов. Практически анализу подвергаются только обладающие конечной длительностью отрезки реализаций, и если на этих отрезках времени исследуемые процессы мало отличаются от стационарных, то к ним можно применять теорию стационарных процессов.

Различают стационарность в узком и широком смысле.

Стационарным в узком смысле называют процесс x(t), если его n-мерная плотность вероятности при любом n зависит только от величины интервалов t₂ - t₁,...,t _n - t₁ и не зависит от положения этих интервалов в области изменения аргумента t.

Стационарным в широком смысле называют процесс x(t), математическое ожидание которого постоянно:

(8.19)

а корреляционная функция R_x(t₁,t₂) зависит только от разности ; при этом корреляционную функцию обозначают

. (8.20)

а)

б)

в)

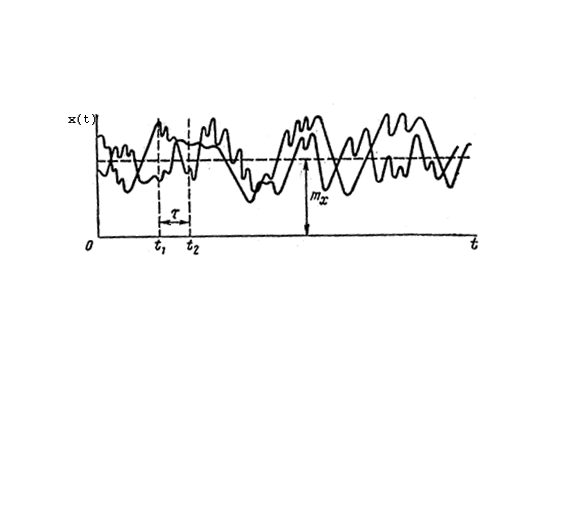
Рис. 8.3. Графики случайного процесса:

а — стационарного; б — нестационарного;

в—стационарного, но не эргодического

Для стационарного процесса x(t) дисперсия

При изучении стационарных процессов можно ограничиваться процессами с математическим ожиданием, равным нулю, так как случайный процесс с ненулевым математическим ожиданием представляют как сумму процесса с нулевым математическим ожиданием и постоянной неслучайной величиной математического ожидания.

На рис. 8.3, а математическое ожидание для стационарного случайного процесса показано в виде горизонтальной прямой m_x = const в отличие от общего случая, приведенного на рис. 8.3, б.Рассеяние значений переменной x(t), характеризуемое величиной , также все время одинаково.

Выполнение условий (8.19) и (8.20) может служить проверкой стационарности случайного процесса.

8.3.2. Эргодические случайные процессы

Существуют стационарные процессы, которые обладают свойством эргодичности: статистические характеристики, полученные осреднением по времени одной реализации (в достаточно большом интервале наблюдения), приближенно совпадают с характеристиками, полученными осреднением по множеству реализаций (при фиксированном времени). Это положение основано на том, что раз статистические характеристики стационарного случайного процесса с течением времени не меняются, то наблюдение случайного процесса на одном объекте в течение длительного времени дает в среднем такую же картину, как незначительное число наблюдений, проведенных в один и тот же момент времени на большом числе объектов одного типа. Иными словами, отдельная реализация процесса на бесконечном промежутке времени полностью определяет весь случайный процесс с его бесчисленными реализациями. Следовательно, для определения статистических характеристик можно ограничиться одним опытом, проводимым в течение достаточно большого интервала времени, т. е. ограничиться обработкой одной реализации вместо множества опытов, необходимых для определения характеристик процесса, не обладающего свойствами эргодичности. Стационарная случайная функция x(t) эргодична, если ее корреляционная функция неограниченно убывает по модулю при .

Свойство эргодичности весьма важно для решения практических задач. Многие стационарные случайные процессы, встречающиеся на практике, обладают свойством эргодичности.

Основные статистические характеристики стационарной случайной функции x(t), обладающей эргодическим свойством, определяются следующими выражениями. Математическое ожидание, или среднее значение имеет вид

, (8.21)

где - усреднение по множеству реализаций;

- усреднение по времени одной реализации (при достаточно большом Т),

— реализация стационарного случайного процесса, взятого на интервале -T<=t<=T, а вне этого интервала рав­ная нулю.

Выражение (8.21) означает, что для процесса, обладающего эргодическими свойствами, среднее по множеству реализаций равно среднему по времени для одной реализации. Чем больше интервал -T<=t<=T, тем точнее можно определить математическое ожидание. Дисперсия случайной функции

. (8.22)

Корреляционная функция, характеризующая связь между значениями случайной функции в моменты x(t) и , может быть определена для стационарного эргодического процесса по одной его реализации, как среднее по времени от произведения случайных функций x(t) и , сдвинутых относительно друг друга на определенный промежуток времени (рис. 8.3):

(8.24)

Если , то корреляционная функция равна диспер­сии случайной функции:

. (8.25)

Корреляционная функция является более общей характеристикой случайного процесса, чем дисперсия, так как дисперсия отображает только начальную ординату графика корреляционной функции. Для многих случайных процессов при очень малых вероятность того, что значение функции мало отличается от значения , близка к единице, т.е. близка к достоверности. По мере увеличения , связь между значениями x(t) и ослабевает, они делаются взаимно независимыми, и функция стремится к нулю.

Для оценки свойств корреляционных функций иногда вводят понятие времени корреляции. Интервал между двумя сечениями x(t) и , начиная с которого можно практически считать некоррелированными случайные величины x(t) и , называют временем корреляции . Иными словами время корреляции - это отрезок на оси ,за пределами которого корреляционная функция R() практически равна нулю. На рис.8.4 приведена корреляционная функция сигнала на входе системы автосопровождения цели. В последнем случае по оси ординат на графике отложено нормированное значение корреляционной функции.

Нормализация позволяет сопоставлять независимо от того, равны или отличаются среднеквадратические значения. Очевидно, что и . Время корреляции может быть нормированной корреляционной функции становятся при меньше достаточно малого числа, например 0,05.

Взаимная корреляционная функция двух случайных, но взаимно зависимых процессов определяется по формуле

. (8.26)

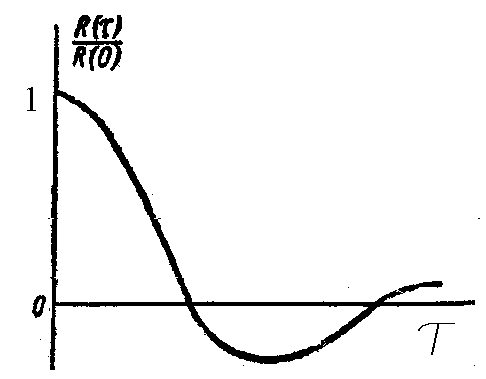
Рис. 8.4. Примерный вид нормированной корреляционной функции

флуктуации, отраженных от цели сигналов

Для статистически независимых процессов x и y взаимная корреляционная функция равна нулю. Однако обратный вывод о том, что если взаимная корреляционная функция равна нулю, то процессы независимы, можно сделать лишь в отдельных случаях (в частности, для процессов с нормальным законом распределения). Общей же силы обратный вывод не имеет.

Лекция 24

План лекции:

1.Спектральная плотность стационарного эргодического процесса.

2.Свойства корреляционных функций и спектральных

плоскостей стационарного эргодического процесса.

4. Рекомендуемая литература [9].