8.2.2. Математическое ожидание, дисперсия

и корреляционная функция случайного процесса

Зная одномерное распределение вероятности, можно определить математическое ожидание m(t) случайной функции x(t) или одномерный момент первого порядка:

(8.9)

где P₁ (x, t) — плотность вероятности, x(t) — случайная функция.

Математическим ожиданием или средним (по множеству) значением случайной функции x(t) называют среднеарифметическое значение бесконечного множества реализаций, т. е. это такая неслучайная функция m_x(t), вокруг которой группируются все реализации данного случайного процесса и которая полностью определяется одномерным законом распределения.

Разность называют центрированной случайной функцией.

Математическое ожидание центрированной случайной функции тождественно равно нулю:

.

В дальнейшем будем рассматривать только центрированные случайные функции и кружочек над х опускается.

Практически математическое ожидание может быть определено по реализациям. Для этого фиксируется значение аргумента t. Тогда при t=t₁ значение реализаций x₁(t₁), x₂(t₁),..., x_N (t₁) представляет собой обычную случайную величину. Математическое ожидание случайной величины находим как среднеарифметическое значение:

(8.10)

где i = 1, 2,..., n – фиксированное значение времени; = 1, 2,…, N - номер реализации.

На основании подсчета, проведенного для различных t=t_i, можно построить график m_x(t_i).

Среднее значение не полностью характеризует случайный процесс. При равных средних значениях процессы могут иметь различные отклонения. Поэтому для характеристики случайного процесса вводится понятие дисперсии.

Дисперсией случайной функции x(t) называют неслучайную и неотрицательную функцию аргумента t, представляющую собой среднее значение квадрата разности между случайной функцией и ее средним значением, или среднее значение квадрата отклонения случайной функции от ее среднего значения.

. (8.11)

Она характеризует интенсивность отклонений относительно среднего значения и, так же как математическое ожидание, определяется одномерным законом распределения. Размерность дисперсии равна квадрату размерности случайной величины. Дисперсия регулярной функции равна нулю.

Среднеквадратическое отклонение равно корню квадратному из дисперсии:

. (8.12)

Введенные понятия иллюстрируются рис. 8.2. Математическое ожидание случайного процесса x(t) представляет собой некоторую среднюю кривую, около которой располагаются все возможные отдельные реализации этого процесса, а дисперсия D_x(t) или среднеквадратическое отклонение характеризует рассеяние отдельных возможных реализаций около этой средней кривой. В общем случае среднеквадратическое отклонение меняется с течением времени. Указанные характеристики m(t) и D(t) для каждого данного момента времени являются средними по множеству.

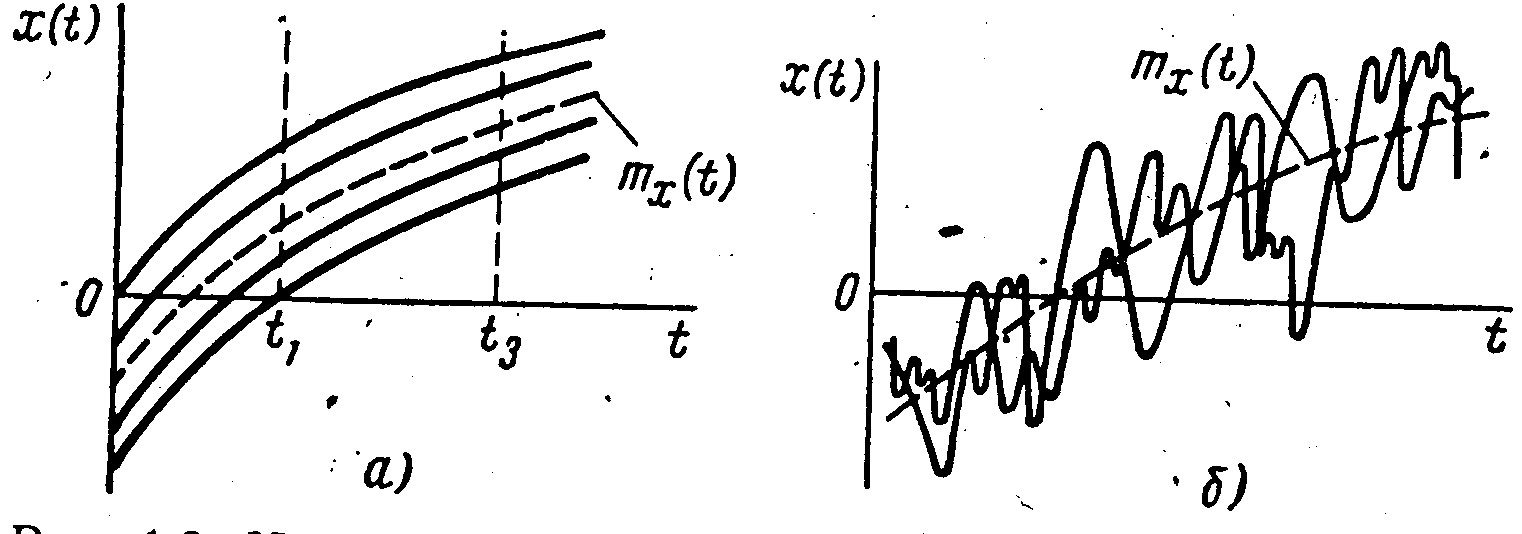
Рис. 8.2. Изменение среднего значения и отдельных реализаций

случайного процесса:

а - при сильной связи между значениями случайной функции;

б - при слабой связи

При обработке результатов испытаний дисперсия случайной функции рассчитывается по реализациям с помощью формулы

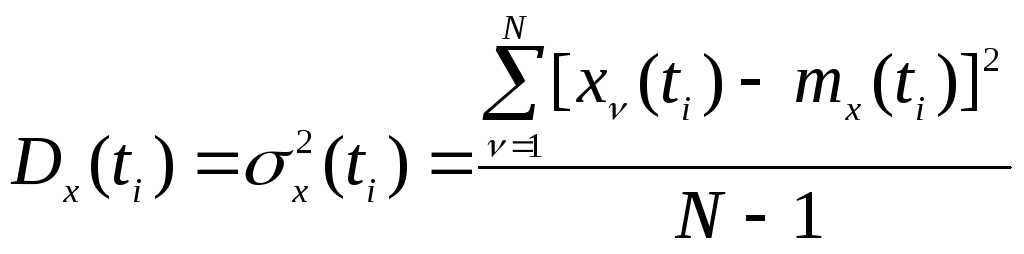. (8.13)

Для случайной функции одномерное распределение вероятности и получаемые на ее основе характеристики (математическое ожидание и дисперсия) еще не являются достаточными для оценки случайного процесса во времени.

Необходимо установить связь между значениями случайного процесса в разные моменты времени. На рис. 8.2 приведены реализации двух случайных функций, которые имеют равные математические ожидания и дисперсии, но по характеру отличаются друг от друга. Если случайная функция (см. рис. 8.2, а) при некотором t приняла значение, лежащее выше m(t), то можно утверждать, что и ближайшее значение реализации случайной функции пройдет выше m(t). Во втором случае (рис. 8.2, б) этого может и не быть. Значит, разница между рассматриваемыми случайными функциями проявляется в характере связи между значениями случайной функции для различных аргументов t₁ и t₂.

Зная двумерную функцию распределения p₂(x₁,t₁;x₂,t₂), можно определить не только математическое ожидание m_x(t) и дисперсию D(t), но и момент второго порядка, характеризующий связь между значениями случайной функции в различные моменты времени.

Математическое ожидание произведения значений центрированной случайной функции, взятых при двух моментах времени t₁ и t₂ называют корреляционной или автокорреляционной функцией:

(8.14)

В этом выражении P₂(x₁,t₁;x₂,t₂) определяет вероятность того, что в момент времени t₁ значение случайного процесса находится в пределах , а в момент времени t₂—в пределах .

Если аргументы корреляционной функции равны между собой (t₁=t₂=t), то

(8.15)

т. е. корреляционная функция для одного и того же сечения равна математическому ожиданию квадрата случайной функции. Для центрированной функции x(t) при t₁=t₂=t будем иметь

т. е. корреляционная функция равна дисперсии случайной функции.

Для характеристики статистической взаимосвязи различных случайных функций, действующих на одну и ту же систему, пользуются понятиями совместного распределения вероятности и взаимной корреляционной функ­ции. Для функций f(t) и совместная функция распределения вероятности имеет вид

. (8.16)

и означает вероятность того, что в момент времени t=t₁ значение f(t₁) меньше f, а в момент времени t=t₂ зна­чение меньше . Совместная плотность вероятности

. (8.17)

Соответственно взаимной корреляционной функцией двух случайных центрированных функций f и называется математическое ожидание произведения этих функций, взятых при различном времени:

. (8.18)

Случайные функции называют коррелированными, если их взаимная корреляционная функция не равна тождественно нулю, и некоррелированными при равенстве ее нулю.