7. Методы синтеза, основанные на теории

ПРОСТРАНСТВА СОСТОЯНИЙ

ЛЕКЦИЯ 20

План лекции:

1. Рассказать о составлении уравнений САУ в пространстве состоя­ний.

2. Рассмотреть пример.

3. Рекомендуемая литература [4, 6].

7.1. Уравнения системы в пространстве состояний

При исследовании динамических свойств САУ классическими методами после составления дифференциальных уравнений для отдельных элементов системы обычно переходят к передаточным функциям. Да­лее составляют общую структурную схему САУ, в которой отдельные элементы представляются блоками с соот­ветствующими передаточными функциями. Затем определяют пе­редаточную функцию замкнутой системы, характеризующую связь между изображениями по Лапласу входной и выходной величины САУ.

Поведение системы во времени можно характеризо­вать не только выходной величиной САУ, но и промежуточ­ными переменными в цепи системы, число которых равно порядку системы n. Таким образом, получается n-мерный вектор состоя­ния, множество возможных положений которого образует вектор­ное пространство, называемое пространством состояний системы.

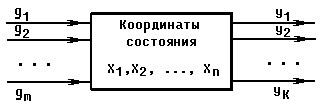
Рис. 7.1

Будем рассматривать общий случай обыкновенных линейных САУ

(рис. 7.1), описываемых системой дифферен­циальных уравнений в нормальной форме в векторно-матричной записи

; (7.1)

Y = CX ,

где X - вектор состояния системы, Y - вектор выходных вели­чин, G - вектор внешних воздействии (задающих и возмущающих), т.е:

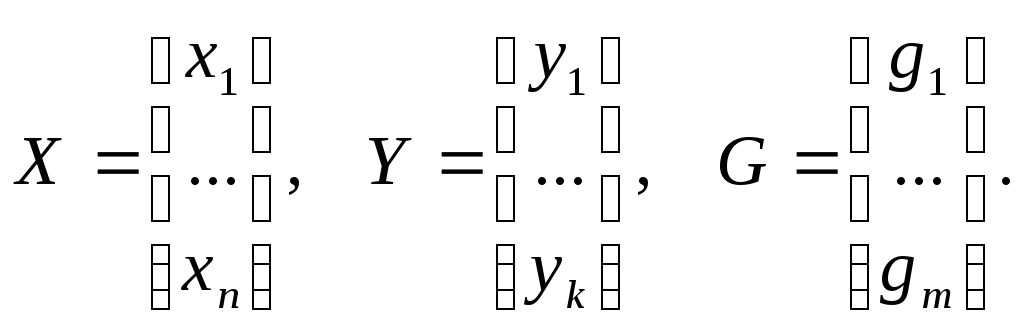
Через А, В, С обозначены:

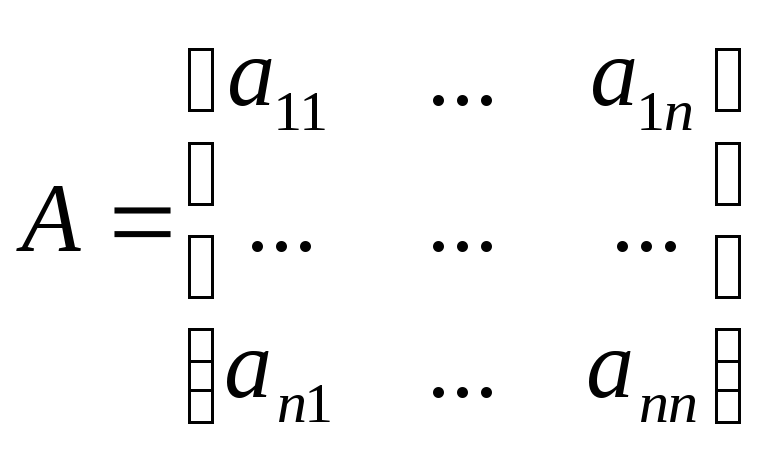- собственная параметрическая матрица САУ;

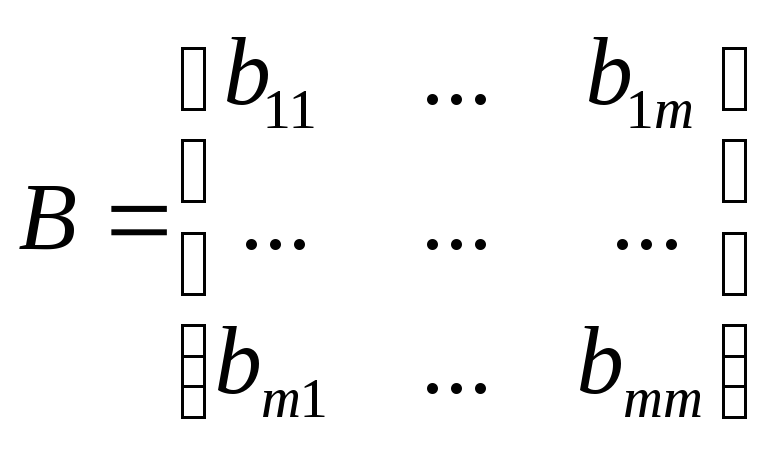- входная матрица САУ;

- выходная матрица САУ.

Процессы в системе при свободном движении (без внешних воздействий) согласно (7.1) описываются векторно-матричным уравнением вида

, (7.2)

которое имеет следующее характеристическое уравнение:

. (7.3)

В развернутой форме векторное уравнение (7.2) записывается следующей системой дифференциальных уравнений:

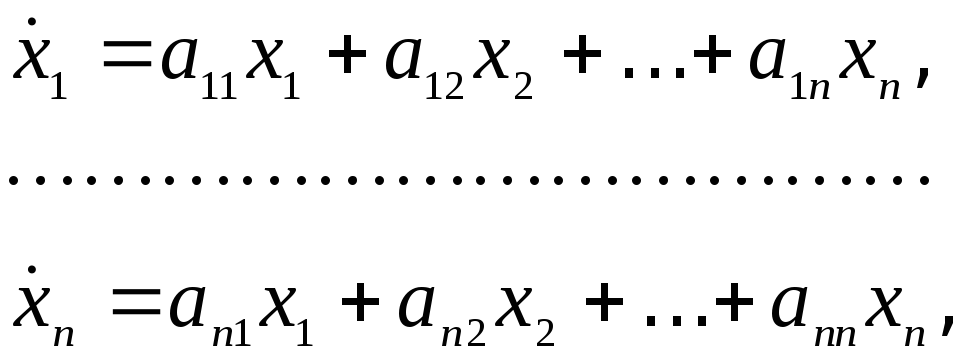(7.4)

Характеристическое уравнение (7.3) в развернутой форме имеет вид

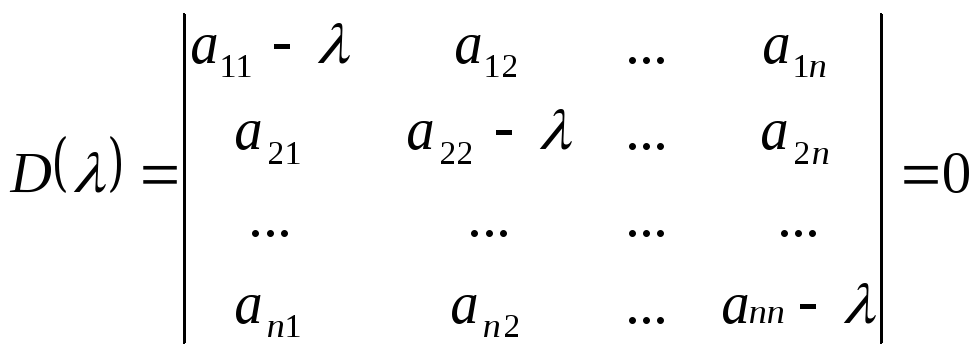. (7.5)

В качестве примера рассмотрим вывод уравнений состояния электромеханической следящей системы, принципиальная схема которой приведена на рис. 7.2.

Рис. 7.2

В этой системе введены обратные связи по углу поворота, ско­рости вращения и току в цепи якоря двигателя. Обозначение переменных ясны из чертежа.

Для электродвигателя постоянного тока имеем:

1) уравнение электрической цепи

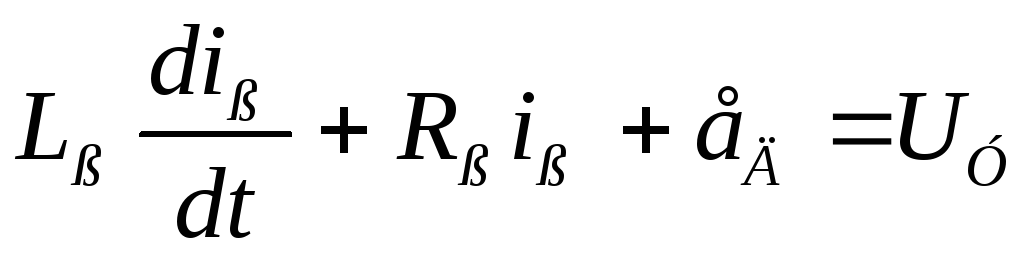; (7.6)

2) уравнение механической цепи

, (7.7)

где М_С=γΩ - момент сопротивления ; М_Д=k_М i_Я - момент двигателя; е_Д=k_E Ω – противо-э.д.с двигателя .

Через γ, k_М, k_E обозначены соответствующие коэффициенты.

Преобразуя выражения (7.6) и (7.7), получим уравнения двигателя в виде

; (7.8)

. (7.9)

Для входной цепи усилителя напряжения имеем

,

где _о , Ω_о – внешние входные воздействия (угол и угловая скорость поворота задающего вала);

, Ω – выходные величины системы (угол и угловая скорость поворота выходного вала).

Для входной цепи усилителя мощности запишем

U₂ = K₁U₁ - K_ocU_oc,

где U_oc=R_ш i_Я .

Выходное напряжение усилителя мощности УМ, с учетом предыдущего выражения, будет равно

U_у = K_умU₂=К_умК₁U₁ - K_умK_осR_шi_Я.

После подстановки получим

U_у = K_умK₁[К_П(_о - )+К_Т(Ω_о-Ω)]-K_умK_осR_шi_Я. (7.10)

Совместно (7.8) и (7.10) дают уравнение

которое может быть представлено в виде

.(7.11)

Скорость вращения

. (7.12)

Систему из трех уравнений (7.11), (7.9) и (7.12) запишем в векторно-матричной форме:

.

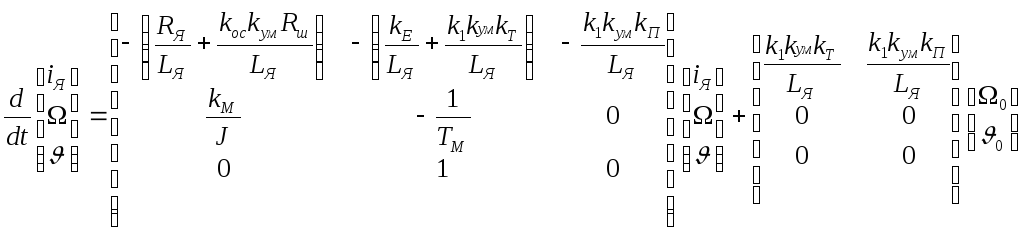Введем обозначения i_Я=x₁; Ω=x₂; =x₃ – координаты вектора состояний следящей системы. Обозначим также :

В результате получим уравнение состояний следящей системы в стандартной векторно-матричной форме

, (7.13)

где X – вектор состояний системы, G – входной вектор, причем

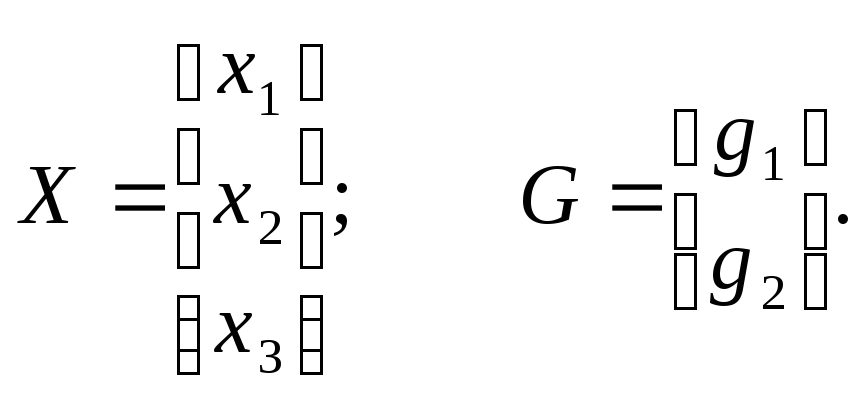
Параметрическая матрица состояния системы А и входная матрица В имеют вид:

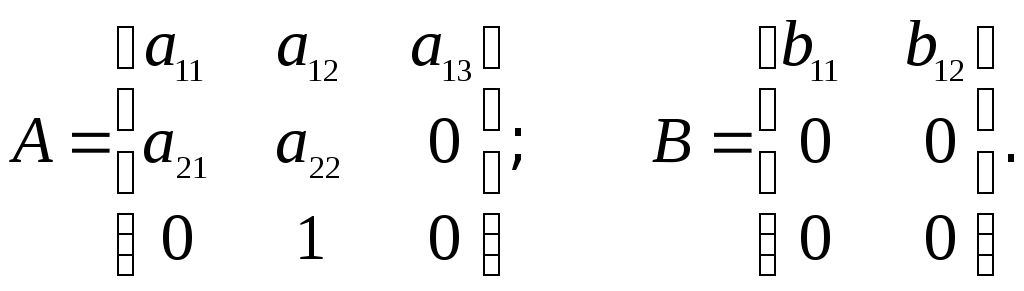
Соответствующая структурная схема cистемы представлена на рис. 7.3.

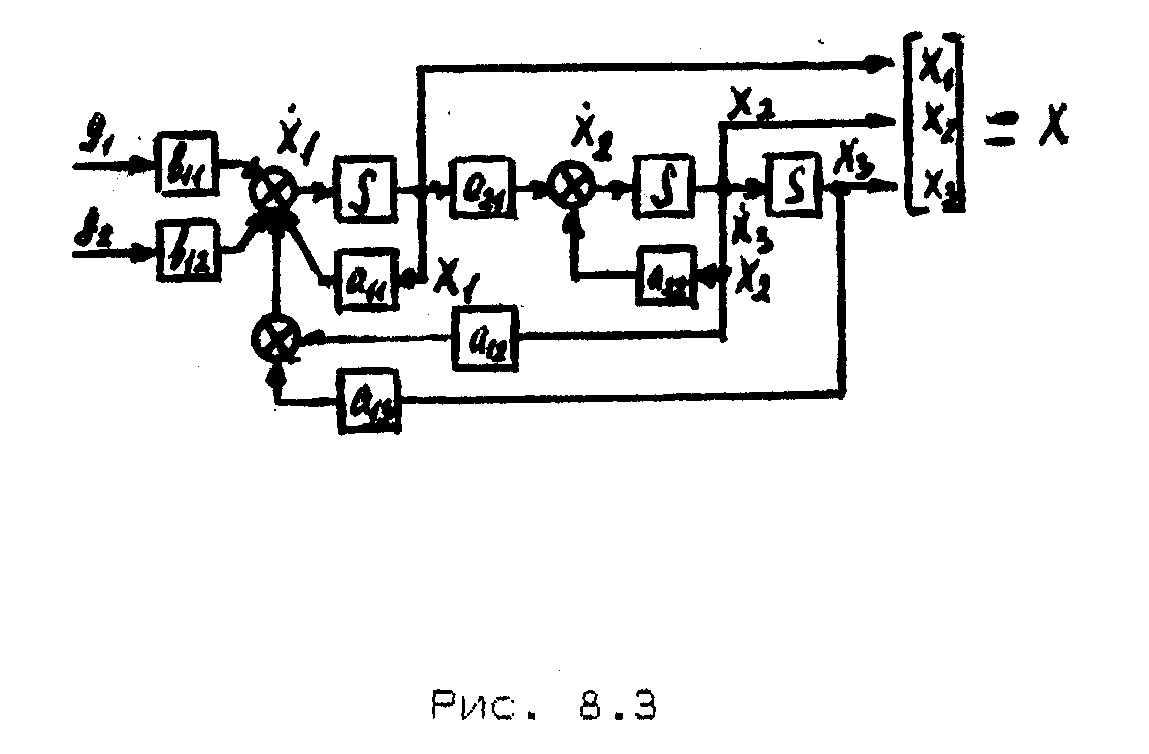
Рис. 7.3

Она составлена по уравнениям вида

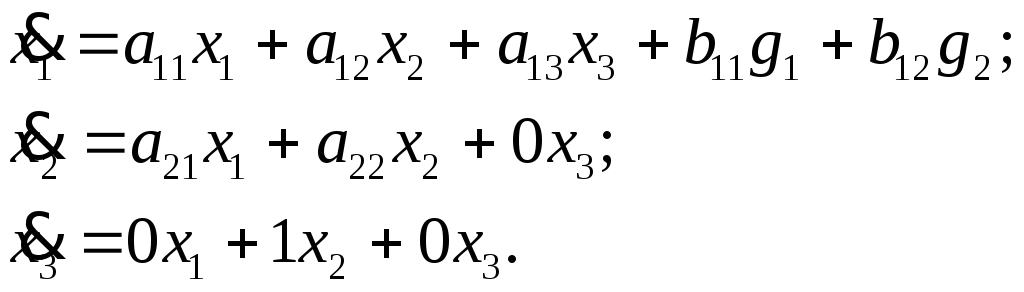
Дополним уравнение (7.13) уравнением выхода.

Y=CX.

Поскольку в наших обозначениях выходные величины Ω=x₂, =x₃, то в этом уравнении координатами выходного вектора системы

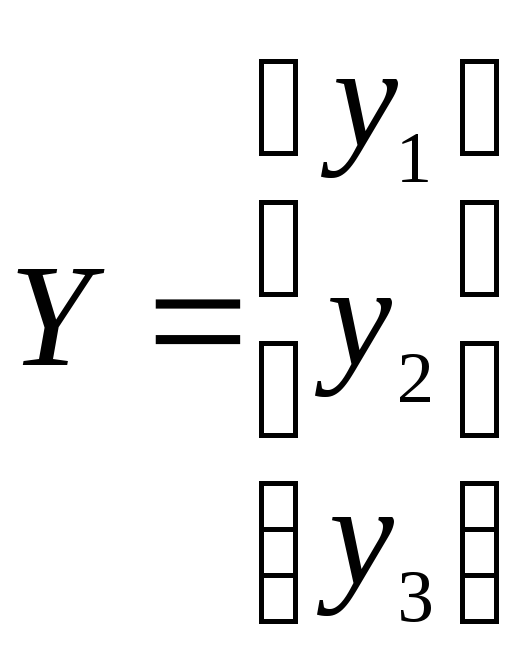
будут величины y₁=0, y₂=x₂= Ω, y₃=x₃=, поэтому выходная мат­рица системы будет иметь вид

.

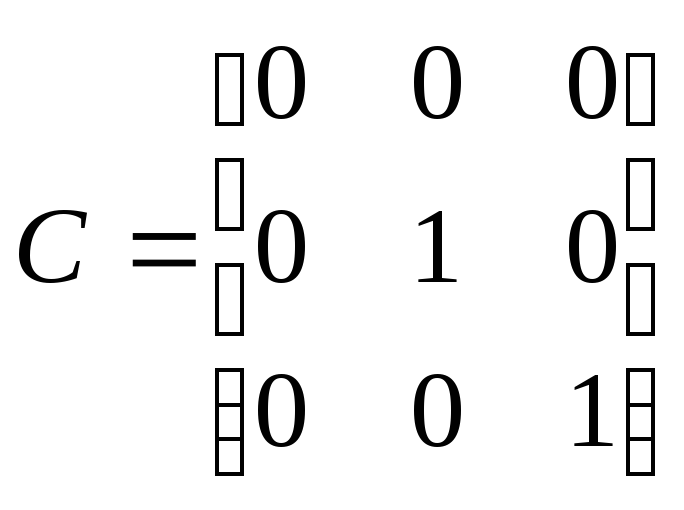Таким образом, при введении в систему корректирующих фильтров за счет дополнения основных уравнений системы уравнениями цепей коррекции, пространство состояний корректируе­мой системы расширяется. Порядок системы увеличивается, од­нако число свободно подбираемых параметров увеличивается еще больше.

В качестве примера составим уравнения состояния интегро-дифференцирующего корректирующего звена (рис. 7.4 и 7.5).

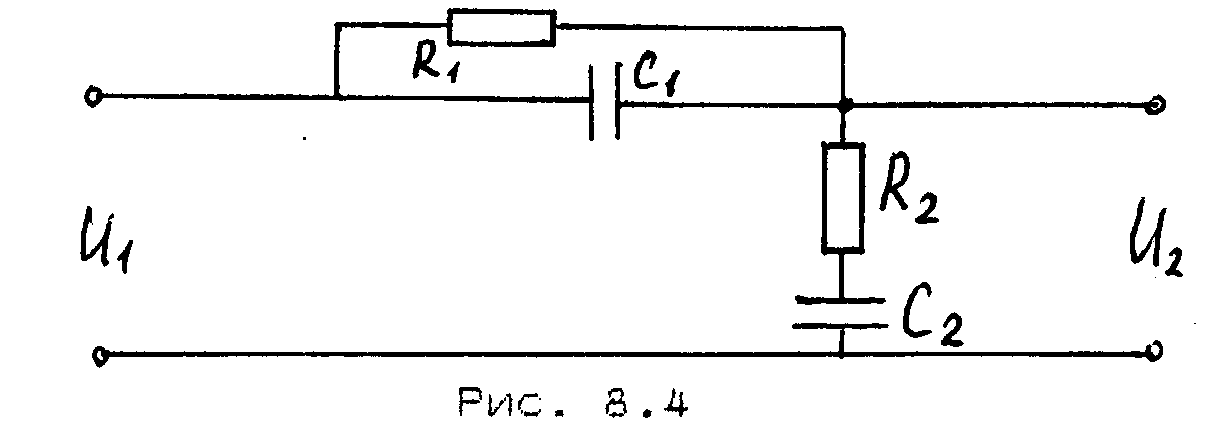
Рис. 7.4

В качестве координат состояния целесообразно выбрать напря­жения на конденсаторах, характеризующие накопление количест­ва электричества. Получим

Но, так как

то после подстановки и простых преобразовании будем иметь следующие уравнения состояния:

.

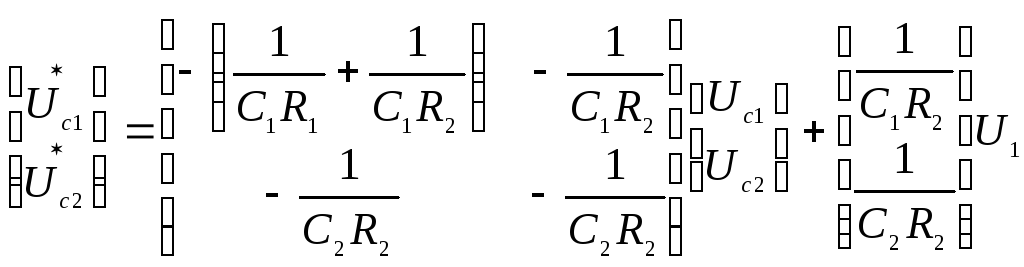Структурная схема в пространстве состояний, составленная по уравнениям данного корректирующего звена, приведена на рис. 7.5

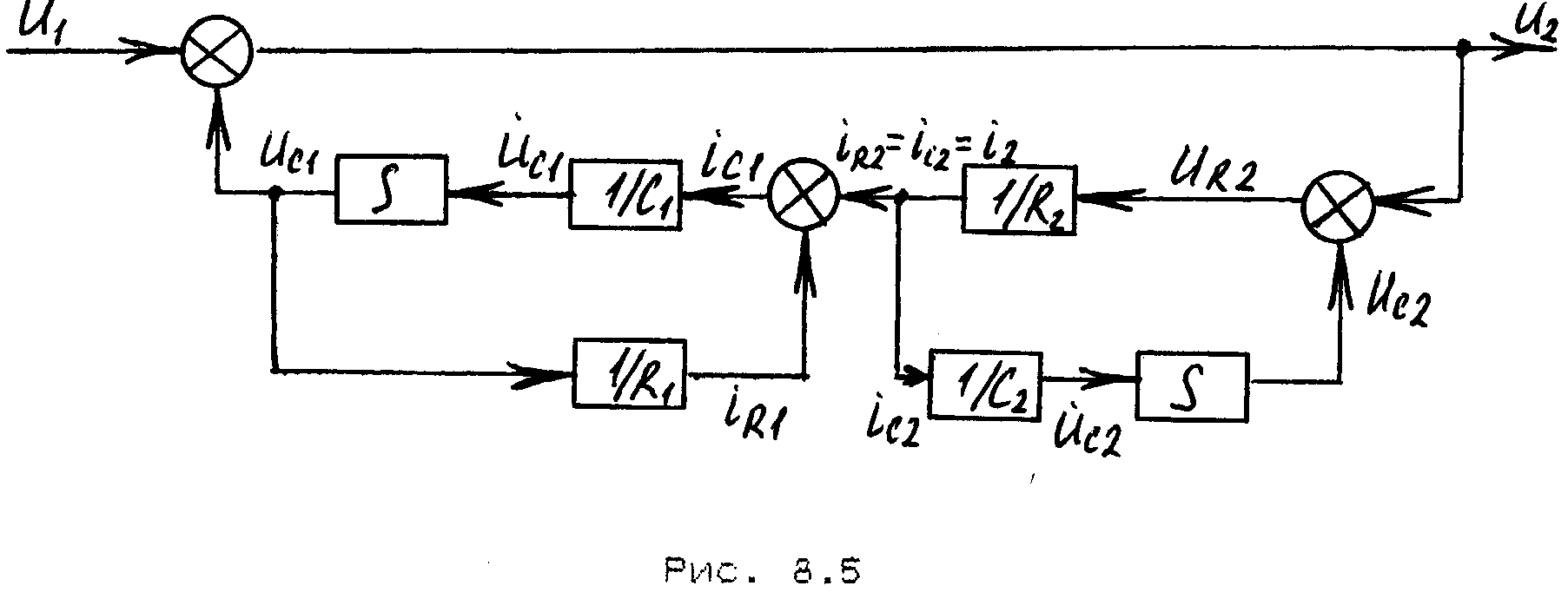
Рис. 7.5

Выходная величина U₂=U₁-U_C1.

Включение последовательно подобранного корректирующего звена расширяет пространство состояний на две координаты, однако число свободных варьируемых параметров С₁, С₂, R₁, R₂ равно четырем.

ЛЕКЦИЯ 21

План лекции:

1. Коррекция системы в пространстве состояния.

2. Корневой метод синтеза САУ по координатам пространства состоянии.

3. Прямой метод синтеза корректирующей обратной связи следя­щей

системы.

4. Рекомендуемая литература [4].