
- •Preface
- •Textbook Layout and Design
- •Preliminaries
- •See, Do, Teach
- •Other Conditions for Learning
- •Your Brain and Learning
- •The Method of Three Passes
- •Mathematics
- •Summary
- •Homework for Week 0
- •Summary
- •1.1: Introduction: A Bit of History and Philosophy
- •1.2: Dynamics
- •1.3: Coordinates
- •1.5: Forces
- •1.5.1: The Forces of Nature
- •1.5.2: Force Rules
- •Example 1.6.1: Spring and Mass in Static Force Equilibrium
- •1.7: Simple Motion in One Dimension
- •Example 1.7.1: A Mass Falling from Height H
- •Example 1.7.2: A Constant Force in One Dimension
- •1.7.1: Solving Problems with More Than One Object
- •Example 1.7.4: Braking for Bikes, or Just Breaking Bikes?
- •1.8: Motion in Two Dimensions
- •Example 1.8.1: Trajectory of a Cannonball
- •1.8.2: The Inclined Plane
- •Example 1.8.2: The Inclined Plane
- •1.9: Circular Motion
- •1.9.1: Tangential Velocity
- •1.9.2: Centripetal Acceleration
- •Example 1.9.1: Ball on a String
- •Example 1.9.2: Tether Ball/Conic Pendulum
- •1.9.3: Tangential Acceleration
- •Homework for Week 1
- •Summary
- •2.1: Friction
- •Example 2.1.1: Inclined Plane of Length L with Friction
- •Example 2.1.3: Find The Minimum No-Skid Braking Distance for a Car
- •Example 2.1.4: Car Rounding a Banked Curve with Friction
- •2.2: Drag Forces
- •2.2.1: Stokes, or Laminar Drag
- •2.2.2: Rayleigh, or Turbulent Drag
- •2.2.3: Terminal velocity
- •Example 2.2.1: Falling From a Plane and Surviving
- •2.2.4: Advanced: Solution to Equations of Motion for Turbulent Drag
- •Example 2.2.3: Dropping the Ram
- •2.3.1: Time
- •2.3.2: Space
- •2.4.1: Identifying Inertial Frames
- •Example 2.4.1: Weight in an Elevator
- •Example 2.4.2: Pendulum in a Boxcar
- •2.4.2: Advanced: General Relativity and Accelerating Frames
- •2.5: Just For Fun: Hurricanes
- •Homework for Week 2
- •Week 3: Work and Energy
- •Summary
- •3.1: Work and Kinetic Energy
- •3.1.1: Units of Work and Energy
- •3.1.2: Kinetic Energy
- •3.2: The Work-Kinetic Energy Theorem
- •3.2.1: Derivation I: Rectangle Approximation Summation
- •3.2.2: Derivation II: Calculus-y (Chain Rule) Derivation
- •Example 3.2.1: Pulling a Block
- •Example 3.2.2: Range of a Spring Gun
- •3.3: Conservative Forces: Potential Energy
- •3.3.1: Force from Potential Energy
- •3.3.2: Potential Energy Function for Near-Earth Gravity
- •3.3.3: Springs
- •3.4: Conservation of Mechanical Energy
- •3.4.1: Force, Potential Energy, and Total Mechanical Energy
- •Example 3.4.1: Falling Ball Reprise
- •Example 3.4.2: Block Sliding Down Frictionless Incline Reprise
- •Example 3.4.3: A Simple Pendulum
- •Example 3.4.4: Looping the Loop
- •3.5: Generalized Work-Mechanical Energy Theorem
- •Example 3.5.1: Block Sliding Down a Rough Incline
- •Example 3.5.2: A Spring and Rough Incline
- •3.5.1: Heat and Conservation of Energy
- •3.6: Power
- •Example 3.6.1: Rocket Power
- •3.7: Equilibrium
- •3.7.1: Energy Diagrams: Turning Points and Forbidden Regions
- •Homework for Week 3
- •Summary
- •4.1: Systems of Particles
- •Example 4.1.1: Center of Mass of a Few Discrete Particles
- •4.1.2: Coarse Graining: Continuous Mass Distributions
- •Example 4.1.2: Center of Mass of a Continuous Rod
- •Example 4.1.3: Center of mass of a circular wedge
- •4.2: Momentum
- •4.2.1: The Law of Conservation of Momentum
- •4.3: Impulse
- •Example 4.3.1: Average Force Driving a Golf Ball
- •Example 4.3.2: Force, Impulse and Momentum for Windshield and Bug
- •4.3.1: The Impulse Approximation
- •4.3.2: Impulse, Fluids, and Pressure
- •4.4: Center of Mass Reference Frame
- •4.5: Collisions
- •4.5.1: Momentum Conservation in the Impulse Approximation
- •4.5.2: Elastic Collisions
- •4.5.3: Fully Inelastic Collisions
- •4.5.4: Partially Inelastic Collisions
- •4.6: 1-D Elastic Collisions
- •4.6.1: The Relative Velocity Approach
- •4.6.2: 1D Elastic Collision in the Center of Mass Frame
- •4.7: Elastic Collisions in 2-3 Dimensions
- •4.8: Inelastic Collisions
- •Example 4.8.1: One-dimensional Fully Inelastic Collision (only)
- •Example 4.8.2: Ballistic Pendulum
- •Example 4.8.3: Partially Inelastic Collision
- •4.9: Kinetic Energy in the CM Frame
- •Homework for Week 4
- •Summary
- •5.1: Rotational Coordinates in One Dimension
- •5.2.1: The r-dependence of Torque
- •5.2.2: Summing the Moment of Inertia
- •5.3: The Moment of Inertia
- •Example 5.3.1: The Moment of Inertia of a Rod Pivoted at One End
- •5.3.1: Moment of Inertia of a General Rigid Body
- •Example 5.3.2: Moment of Inertia of a Ring
- •Example 5.3.3: Moment of Inertia of a Disk
- •5.3.2: Table of Useful Moments of Inertia
- •5.4: Torque as a Cross Product
- •Example 5.4.1: Rolling the Spool
- •5.5: Torque and the Center of Gravity
- •Example 5.5.1: The Angular Acceleration of a Hanging Rod
- •Example 5.6.1: A Disk Rolling Down an Incline
- •5.7: Rotational Work and Energy
- •5.7.1: Work Done on a Rigid Object
- •5.7.2: The Rolling Constraint and Work
- •Example 5.7.2: Unrolling Spool
- •Example 5.7.3: A Rolling Ball Loops-the-Loop
- •5.8: The Parallel Axis Theorem
- •Example 5.8.1: Moon Around Earth, Earth Around Sun
- •Example 5.8.2: Moment of Inertia of a Hoop Pivoted on One Side
- •5.9: Perpendicular Axis Theorem
- •Example 5.9.1: Moment of Inertia of Hoop for Planar Axis
- •Homework for Week 5
- •Summary
- •6.1: Vector Torque
- •6.2: Total Torque
- •6.2.1: The Law of Conservation of Angular Momentum
- •Example 6.3.1: Angular Momentum of a Point Mass Moving in a Circle
- •Example 6.3.2: Angular Momentum of a Rod Swinging in a Circle
- •Example 6.3.3: Angular Momentum of a Rotating Disk
- •Example 6.3.4: Angular Momentum of Rod Sweeping out Cone
- •6.4: Angular Momentum Conservation
- •Example 6.4.1: The Spinning Professor
- •6.4.1: Radial Forces and Angular Momentum Conservation
- •Example 6.4.2: Mass Orbits On a String
- •6.5: Collisions
- •Example 6.5.1: Fully Inelastic Collision of Ball of Putty with a Free Rod
- •Example 6.5.2: Fully Inelastic Collision of Ball of Putty with Pivoted Rod
- •6.5.1: More General Collisions
- •Example 6.6.1: Rotating Your Tires
- •6.7: Precession of a Top
- •Homework for Week 6
- •Week 7: Statics
- •Statics Summary
- •7.1: Conditions for Static Equilibrium
- •7.2: Static Equilibrium Problems
- •Example 7.2.1: Balancing a See-Saw
- •Example 7.2.2: Two Saw Horses
- •Example 7.2.3: Hanging a Tavern Sign
- •7.2.1: Equilibrium with a Vector Torque
- •Example 7.2.4: Building a Deck
- •7.3: Tipping
- •Example 7.3.1: Tipping Versus Slipping
- •Example 7.3.2: Tipping While Pushing
- •7.4: Force Couples
- •Example 7.4.1: Rolling the Cylinder Over a Step
- •Homework for Week 7
- •Week 8: Fluids
- •Fluids Summary
- •8.1: General Fluid Properties
- •8.1.1: Pressure
- •8.1.2: Density
- •8.1.3: Compressibility
- •8.1.5: Properties Summary
- •Static Fluids
- •8.1.8: Variation of Pressure in Incompressible Fluids
- •Example 8.1.1: Barometers
- •Example 8.1.2: Variation of Oceanic Pressure with Depth
- •8.1.9: Variation of Pressure in Compressible Fluids
- •Example 8.1.3: Variation of Atmospheric Pressure with Height
- •Example 8.2.1: A Hydraulic Lift
- •8.3: Fluid Displacement and Buoyancy
- •Example 8.3.1: Testing the Crown I
- •Example 8.3.2: Testing the Crown II
- •8.4: Fluid Flow
- •8.4.1: Conservation of Flow
- •Example 8.4.1: Emptying the Iced Tea
- •8.4.3: Fluid Viscosity and Resistance
- •8.4.4: A Brief Note on Turbulence
- •8.5: The Human Circulatory System
- •Example 8.5.1: Atherosclerotic Plaque Partially Occludes a Blood Vessel
- •Example 8.5.2: Aneurisms
- •Homework for Week 8
- •Week 9: Oscillations
- •Oscillation Summary
- •9.1: The Simple Harmonic Oscillator
- •9.1.1: The Archetypical Simple Harmonic Oscillator: A Mass on a Spring
- •9.1.2: The Simple Harmonic Oscillator Solution
- •9.1.3: Plotting the Solution: Relations Involving
- •9.1.4: The Energy of a Mass on a Spring
- •9.2: The Pendulum
- •9.2.1: The Physical Pendulum
- •9.3: Damped Oscillation
- •9.3.1: Properties of the Damped Oscillator
- •Example 9.3.1: Car Shock Absorbers
- •9.4: Damped, Driven Oscillation: Resonance
- •9.4.1: Harmonic Driving Forces
- •9.4.2: Solution to Damped, Driven, Simple Harmonic Oscillator
- •9.5: Elastic Properties of Materials
- •9.5.1: Simple Models for Molecular Bonds
- •9.5.2: The Force Constant
- •9.5.3: A Microscopic Picture of a Solid
- •9.5.4: Shear Forces and the Shear Modulus
- •9.5.5: Deformation and Fracture
- •9.6: Human Bone
- •Example 9.6.1: Scaling of Bones with Animal Size
- •Homework for Week 9
- •Week 10: The Wave Equation
- •Wave Summary
- •10.1: Waves
- •10.2: Waves on a String
- •10.3: Solutions to the Wave Equation
- •10.3.1: An Important Property of Waves: Superposition
- •10.3.2: Arbitrary Waveforms Propagating to the Left or Right
- •10.3.3: Harmonic Waveforms Propagating to the Left or Right
- •10.3.4: Stationary Waves
- •10.5: Energy
- •Homework for Week 10
- •Week 11: Sound
- •Sound Summary
- •11.1: Sound Waves in a Fluid
- •11.2: Sound Wave Solutions
- •11.3: Sound Wave Intensity
- •11.3.1: Sound Displacement and Intensity In Terms of Pressure
- •11.3.2: Sound Pressure and Decibels
- •11.4: Doppler Shift
- •11.4.1: Moving Source
- •11.4.2: Moving Receiver
- •11.4.3: Moving Source and Moving Receiver
- •11.5: Standing Waves in Pipes
- •11.5.1: Pipe Closed at Both Ends
- •11.5.2: Pipe Closed at One End
- •11.5.3: Pipe Open at Both Ends
- •11.6: Beats
- •11.7: Interference and Sound Waves
- •Homework for Week 11
- •Week 12: Gravity
- •Gravity Summary
- •12.1: Cosmological Models
- •12.2.1: Ellipses and Conic Sections
- •12.4: The Gravitational Field
- •12.4.1: Spheres, Shells, General Mass Distributions
- •12.5: Gravitational Potential Energy
- •12.6: Energy Diagrams and Orbits
- •12.7: Escape Velocity, Escape Energy
- •Example 12.7.1: How to Cause an Extinction Event
- •Homework for Week 12

354 |
Week 8: Fluids |
As mentioned above, the formula for the derivative of pressure with z is unchanged for compressible or incompressible fluids. If we take dP/dz = ρg and multiply both sides by dz as before and integrate, now we get (assuming a fixed temperature T ):
|
dP |
= |
ρg dz |
= |
M g |
P dz |
|||
|
|
||||||||
|
|
|
|
|
|
|
|
RT |
|
|
dP |
|
= |
|
M g |
dz |
|
|
|
|
P |
|
|
|
|
||||
Z |
= |
|
RT |
dz |
|
|
|||
P |
|
RT Z |
|
|
|||||
|
dP |
|
M g |
|
|
|
|||
ln(P ) |
= |
|
M g |
z + C |
|
|
|||
|
|
|
|||||||
|
|
|
|
|
RT |
|
|
|
|
We now do the usual149 – exponentiate both sides, turn the exponential of the sum into the product of exponentials, turn the exponential of a constant of integration into a constant of integration, and match the units:
P (z) = P0e |
( MRTg )z |
(725) |
|
where P0 is the pressure at zero depth, because (recall!) z is measured positive down in our expression for dP/dz.
Example 8.1.3: Variation of Atmospheric Pressure with Height
Using z to describe depth is moderately inconvenient, so let us define the height h above sea level to be −z. In that case P0 is (how about that!) 1 Atmosphere. The molar mass of dry air is M = 0.029 kilograms per mole. R = 8.31 Joules/(mole-K◦). Hence a bit of multiplication at T = 300◦:
M g |
= |
0.029 × 10 |
= 1.12 |
× |
10−4 |
meters−1 |
(726) |
|||
|
RT |
|
||||||||
|
|
8.31 |
× |
300 |
|
|
|
|
||
or: |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
P (h) = 105 exp(−0.00012 h) Pa = 1000 exp(−0.00012 h) mbar |
(727) |
|||||||||
Note well that the temperature of air is not constant as one ascends – it drops by a fairly significant amount, even on the absolute scale (and higher still, it rises by an even greater amount before dropping again as one moves through the layers of the atmosphere. Since the pressure is found from an integral, this in turn means that the exponential behavior itself is rather inexact, but still it isn’t a terrible predictor of the variation of pressure with height. This equation predicts that air pressure should drop to 1/e of its sea-level value of 1000 mbar at a height of around 8000 meters, the height of the so-called death zone150 . We can compare the actual (average) pressure at 8000 meters, 356 mbar, to 1000 × e−1 = 368 mbar. We get remarkably good agreement!
This agreement rapidly breaks down, however, and meteorologists actually use a patchwork of formulae (both algebraic and exponential) to give better agreement to the actual variation of air pressure with height as one moves up and down through the various named layers of the atmosphere with the pressure, temperature and even molecular composition of “air” varying all the way. This simple model explains a lot of the variation, but its assumptions are not really correct.
149Which should be familiar to you both from solving the linear drag problem in Week 2 and from the online Math Review.
150Wikipedia: http://www.wikipedia.org/wiki/E ects of high altitude on humans. This is the height where air pres-
sure drops to where humans are at extreme risk of dying if they climb without supplemental oxygen support – beyond this height hypoxia reduces one’s ability to make important and life-critical decisions during the very last, most stressful, part of the climb. Mount Everest (for example) can only be climbed with oxygen masks and some of the greatest disasters that have occurred climbing it and other peaks are associated with a lack of or failure of supplemental oxygen.
Week 8: Fluids |
355 |
8.2: Pascal’s Principle and Hydraulics
We note that (from the above) the general form of P of a fluid confined to a sealed container has
the most general form:
Z z
P (z) = P0 + ρgdz (728)
0
where P0 is the constant of integration or value of the pressure at the reference depth z = 0. This has an important consequence that forms the basis of hydraulics.
F |
|
|
|
Fp |
P0 |
|
|
|
|
||
Piston |
|
|
|
|
P(z) |
x |
|
z |
z |
||
|
|||
z |
|
|
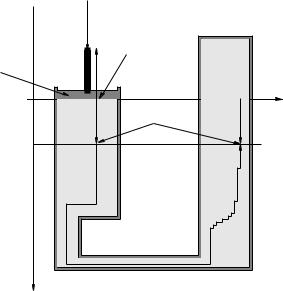
Figure 105: A single piston seated tightly in a frictionless cylinder of cross-sectional area A is used to compress water in a sealed container. Water is incompressible and does not significantly change its volume at P = 1 bar (and a constant room temperature) for pressure changes on the order of 0.1-100 bar.
Suppose, then, that we have an incompressible fluid e.g. water confined within a sealed container by e.g. a piston that can be pushed or pulled on to increase or decrease the confinement pressure on the surface of the piston. Such an arrangement is portrayed in figure 105.
We can push down (or pull back) on the piston with any total downward force F that we like that leaves the system in equilibrium. Since the piston itself is in static equilibrium, the force we push with must be opposed by the pressure in the fluid, which exerts an equal and opposite upwards force:
F = Fp = P0A |
(729) |
where A is the cross sectional area of the piston and where we’ve put the cylinder face at z = 0, which we are obviously free to do. For all practical purposes this means that we can make P0 “anything we like” within the range of pressures that are unlikely to make water at room temperature change it’s state or volume do other bad things, say P = (0.1, 100) bar.
The pressure at a depth z in the container is then (from our previous work):
P (z) = P0 + ρgz |
(730) |
where ρ = ρw if the cylinder is indeed filled with water, but the cylinder could equally well be filled with hydraulic fluid (basically oil, which assists in lubricating the piston and ensuring that it remains “frictionless’ while assisting the seal), alcohol, mercury, or any other incompressible liquid.
356 |
Week 8: Fluids |
We recall that the pressure changes only when we change our depth. Moving laterally does not change the pressure, because e.g. dP/dx = dP/dy = 0. We can always find a path consisting of vertical and lateral displacements from z = 0 to any other point in the container – two such points at the same depth z are shown in 105, along with a (deliberately ziggy-zaggy151) vertical/horizontal path connecting them. Clearly these two points must have the same pressure P (z)!
Now consider the following. Suppose we start with pressure P0 (so that the pressure at these two points is P (z), but then change F to make the pressure P0′ and the pressure at the two points P ′(z). Then:
P (z) = |
P0 + ρgz |
|
|
P ′(z) |
= |
P0′ + ρgz |
|
P (z) |
= |
P ′(z) − P (z) = P0′ − P0 = P0 |
(731) |
That is, the pressure change at depth z does not depend on only on the change in the pressure exerted by the piston!
z at any point in the fluid! It depends
This result is known as Pascal’s Principle and it holds (more or less) for any compressible fluid, not just incompressible ones, but in the case of compressible fluids the piston will move up or down or in or out and the density of the fluid will change and hence the treatment of the integral will be too complicated to cope with. Pascal’s Principle is more commonly given in English words as:
Any change in the pressure exerted at a given point on a confined fluid is transmitted, undiminished, throughout the fluid.
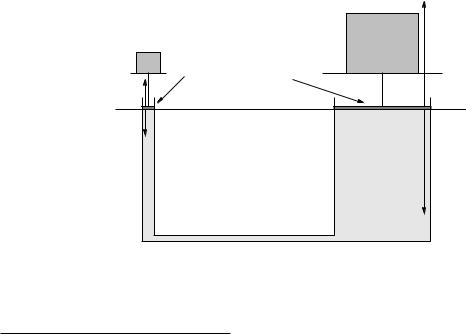
Pascal’s principle is the basis of hydraulics. Hydraulics are a kind of fluid-based simple machine that can be used to greatly amplify an applied force. To understand it, consider the following figure:
Example 8.2.1: A Hydraulic Lift
|
F2 |
|
M |
m |
|
A1 |
A2 |
F1 |
|
mg |
|
|
Mg |
Figure 106: A simple schematic for a hydraulic lift of the sort used in auto shops to lift your car.
Figure 106 illustrates the way we can multiply forces using Pascal’s Principle. Two pistons seal o a pair of cylinders connected by a closed tube that contains an incompressible fluid. The two pistons
151Because we can make the zigs and zags di erentially small, at which point this piecewise horizontal-vertical line becomes an arbitrary curve that remain in the fluid. Multivariate calculus can be used to formulate all of these results more prettily, but the reasoning behind them is completely contained in the picture and this text explanation.
