beginning to accommodate this. Of course, raising the ball slightly at the beginning also increases N so maybe it doesn’t ever slip. So the best we can solve for is the minimum height Hmin it must have to roll without slipping assuming that it doesn’t ever actually slip, and “reality” is probably a bit higher to accommodate or prevent slipping, overcome drag forces, and so on.

With that said, the problem’s solution is exactly the same as before except that in the energy conservation step one has to use:

only a tiny bit higher than needed for a block sliding on a frictionless track.

Really, not all that di cult, right? All it takes is some practice, both redoing these examples on your own and doing the homework and it will all make sense.

5.8: The Parallel Axis Theorem

As we have seen, the moment of inertia of an object or collection of point-like objects is just

i

where ri is the distance between the axis of rotation and the point mass mi in a rigid system, or

Z

I = r2dm (547)

where r is the distance from the axis of rotation to “point mass” dm in the rigid object composed of continuously distributed mass.

However, in the previous section, we saw that the kinetic energy of a rigid object relative to an arbitrary origin can be written as the sum of the kinetic energy of the object itself treated as a total mass located at the (moving) center of mass plus the kinetic energy of the object in the moving center of mass reference frame.

For the particular case where a rigid object rotates uniformly around an axis that is parallel to an axis through the center of mass of the object, that is, in such a way that the angular velocity of the center of mass equals the angular velocity around the center of mass we can derive a theorem, called the Parallel Axis Theorem, that can greatly simplify problem solving while embodying the previous result for the kinetic energies. Let’s see how.

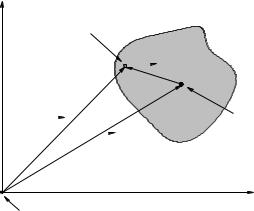
Suppose we want to find the moment of inertia of the arbitrary “blob shaped” rigid mass distribution pictured above in figure 76 about the axis labelled “New (Parallel) Axis”. This is, by

as before!

Warning! This will not work if an object is revolving many times around its own center of mass for each time it revolves around the parallel axis.

Example 5.8.1: Moon Around Earth, Earth Around Sun

This is a conceptual example, not really algebraic. You may have observed that the Moon always keeps the same face towards the Earth – it is said to be “gravitationally locked” by tidal forces so that this is true. This means that the Moon revolves once on its axis in exactly the same amount of time that the Moon itself revolves around the Earth. We could therefore compute the total angular kinetic energy of the Moon by assuming that it is a solid ball of mass M , radius r, in an orbit around the Earth of radius R, and a period of 28.5 days:

All that’s left is the arithmetic.

Contrast this with the Earth rotating around the Sun. It revolves on its own axis 365.25 times during the period in which it revolves around the Sun. To find it’s kinetic energy we could not use the parallel axis theorem, but we can still use the theorem at the end of the previous chapter. Here we would find two di erent angular velocities:

(again, 1 day = 86400 seconds is a good number to remember). Then if we let M be the mass of the Earth, r be its radius, and R be the radius of its orbit around the Sun (all numbers that are readily available on Wikipedia112 we could find the total kinetic energy (relative to the Sun) as:

which is somewhat more complicated, no?

Let’s do a more readily evaluable example:

Example 5.8.2: Moment of Inertia of a Hoop Pivoted on One Side

In figure ?? a hoop of mass M and radius R is pivoted at a point on the side, on the hoop itself, not in the middle. We already know the moment of inertia of the hoop about its center of mass. What

112Wikipedia: http://www.wikipedia.org/wiki/Earth.