
- •Preface
- •Textbook Layout and Design
- •Preliminaries
- •See, Do, Teach
- •Other Conditions for Learning
- •Your Brain and Learning
- •The Method of Three Passes
- •Mathematics
- •Summary
- •Homework for Week 0
- •Summary
- •1.1: Introduction: A Bit of History and Philosophy
- •1.2: Dynamics
- •1.3: Coordinates
- •1.5: Forces
- •1.5.1: The Forces of Nature
- •1.5.2: Force Rules
- •Example 1.6.1: Spring and Mass in Static Force Equilibrium
- •1.7: Simple Motion in One Dimension
- •Example 1.7.1: A Mass Falling from Height H
- •Example 1.7.2: A Constant Force in One Dimension
- •1.7.1: Solving Problems with More Than One Object
- •Example 1.7.4: Braking for Bikes, or Just Breaking Bikes?
- •1.8: Motion in Two Dimensions
- •Example 1.8.1: Trajectory of a Cannonball
- •1.8.2: The Inclined Plane
- •Example 1.8.2: The Inclined Plane
- •1.9: Circular Motion
- •1.9.1: Tangential Velocity
- •1.9.2: Centripetal Acceleration
- •Example 1.9.1: Ball on a String
- •Example 1.9.2: Tether Ball/Conic Pendulum
- •1.9.3: Tangential Acceleration
- •Homework for Week 1
- •Summary
- •2.1: Friction
- •Example 2.1.1: Inclined Plane of Length L with Friction
- •Example 2.1.3: Find The Minimum No-Skid Braking Distance for a Car
- •Example 2.1.4: Car Rounding a Banked Curve with Friction
- •2.2: Drag Forces
- •2.2.1: Stokes, or Laminar Drag
- •2.2.2: Rayleigh, or Turbulent Drag
- •2.2.3: Terminal velocity
- •Example 2.2.1: Falling From a Plane and Surviving
- •2.2.4: Advanced: Solution to Equations of Motion for Turbulent Drag
- •Example 2.2.3: Dropping the Ram
- •2.3.1: Time
- •2.3.2: Space
- •2.4.1: Identifying Inertial Frames
- •Example 2.4.1: Weight in an Elevator
- •Example 2.4.2: Pendulum in a Boxcar
- •2.4.2: Advanced: General Relativity and Accelerating Frames
- •2.5: Just For Fun: Hurricanes
- •Homework for Week 2
- •Week 3: Work and Energy
- •Summary
- •3.1: Work and Kinetic Energy
- •3.1.1: Units of Work and Energy
- •3.1.2: Kinetic Energy
- •3.2: The Work-Kinetic Energy Theorem
- •3.2.1: Derivation I: Rectangle Approximation Summation
- •3.2.2: Derivation II: Calculus-y (Chain Rule) Derivation
- •Example 3.2.1: Pulling a Block
- •Example 3.2.2: Range of a Spring Gun
- •3.3: Conservative Forces: Potential Energy
- •3.3.1: Force from Potential Energy
- •3.3.2: Potential Energy Function for Near-Earth Gravity
- •3.3.3: Springs
- •3.4: Conservation of Mechanical Energy
- •3.4.1: Force, Potential Energy, and Total Mechanical Energy
- •Example 3.4.1: Falling Ball Reprise
- •Example 3.4.2: Block Sliding Down Frictionless Incline Reprise
- •Example 3.4.3: A Simple Pendulum
- •Example 3.4.4: Looping the Loop
- •3.5: Generalized Work-Mechanical Energy Theorem
- •Example 3.5.1: Block Sliding Down a Rough Incline
- •Example 3.5.2: A Spring and Rough Incline
- •3.5.1: Heat and Conservation of Energy
- •3.6: Power
- •Example 3.6.1: Rocket Power
- •3.7: Equilibrium
- •3.7.1: Energy Diagrams: Turning Points and Forbidden Regions
- •Homework for Week 3
- •Summary
- •4.1: Systems of Particles
- •Example 4.1.1: Center of Mass of a Few Discrete Particles
- •4.1.2: Coarse Graining: Continuous Mass Distributions
- •Example 4.1.2: Center of Mass of a Continuous Rod
- •Example 4.1.3: Center of mass of a circular wedge
- •4.2: Momentum
- •4.2.1: The Law of Conservation of Momentum
- •4.3: Impulse
- •Example 4.3.1: Average Force Driving a Golf Ball
- •Example 4.3.2: Force, Impulse and Momentum for Windshield and Bug
- •4.3.1: The Impulse Approximation
- •4.3.2: Impulse, Fluids, and Pressure
- •4.4: Center of Mass Reference Frame
- •4.5: Collisions
- •4.5.1: Momentum Conservation in the Impulse Approximation
- •4.5.2: Elastic Collisions
- •4.5.3: Fully Inelastic Collisions
- •4.5.4: Partially Inelastic Collisions
- •4.6: 1-D Elastic Collisions
- •4.6.1: The Relative Velocity Approach
- •4.6.2: 1D Elastic Collision in the Center of Mass Frame
- •4.7: Elastic Collisions in 2-3 Dimensions
- •4.8: Inelastic Collisions
- •Example 4.8.1: One-dimensional Fully Inelastic Collision (only)
- •Example 4.8.2: Ballistic Pendulum
- •Example 4.8.3: Partially Inelastic Collision
- •4.9: Kinetic Energy in the CM Frame
- •Homework for Week 4
- •Summary
- •5.1: Rotational Coordinates in One Dimension
- •5.2.1: The r-dependence of Torque
- •5.2.2: Summing the Moment of Inertia
- •5.3: The Moment of Inertia
- •Example 5.3.1: The Moment of Inertia of a Rod Pivoted at One End
- •5.3.1: Moment of Inertia of a General Rigid Body
- •Example 5.3.2: Moment of Inertia of a Ring
- •Example 5.3.3: Moment of Inertia of a Disk
- •5.3.2: Table of Useful Moments of Inertia
- •5.4: Torque as a Cross Product
- •Example 5.4.1: Rolling the Spool
- •5.5: Torque and the Center of Gravity
- •Example 5.5.1: The Angular Acceleration of a Hanging Rod
- •Example 5.6.1: A Disk Rolling Down an Incline
- •5.7: Rotational Work and Energy
- •5.7.1: Work Done on a Rigid Object
- •5.7.2: The Rolling Constraint and Work
- •Example 5.7.2: Unrolling Spool
- •Example 5.7.3: A Rolling Ball Loops-the-Loop
- •5.8: The Parallel Axis Theorem
- •Example 5.8.1: Moon Around Earth, Earth Around Sun
- •Example 5.8.2: Moment of Inertia of a Hoop Pivoted on One Side
- •5.9: Perpendicular Axis Theorem
- •Example 5.9.1: Moment of Inertia of Hoop for Planar Axis
- •Homework for Week 5
- •Summary
- •6.1: Vector Torque
- •6.2: Total Torque
- •6.2.1: The Law of Conservation of Angular Momentum
- •Example 6.3.1: Angular Momentum of a Point Mass Moving in a Circle
- •Example 6.3.2: Angular Momentum of a Rod Swinging in a Circle
- •Example 6.3.3: Angular Momentum of a Rotating Disk
- •Example 6.3.4: Angular Momentum of Rod Sweeping out Cone
- •6.4: Angular Momentum Conservation
- •Example 6.4.1: The Spinning Professor
- •6.4.1: Radial Forces and Angular Momentum Conservation
- •Example 6.4.2: Mass Orbits On a String
- •6.5: Collisions
- •Example 6.5.1: Fully Inelastic Collision of Ball of Putty with a Free Rod
- •Example 6.5.2: Fully Inelastic Collision of Ball of Putty with Pivoted Rod
- •6.5.1: More General Collisions
- •Example 6.6.1: Rotating Your Tires
- •6.7: Precession of a Top
- •Homework for Week 6
- •Week 7: Statics
- •Statics Summary
- •7.1: Conditions for Static Equilibrium
- •7.2: Static Equilibrium Problems
- •Example 7.2.1: Balancing a See-Saw
- •Example 7.2.2: Two Saw Horses
- •Example 7.2.3: Hanging a Tavern Sign
- •7.2.1: Equilibrium with a Vector Torque
- •Example 7.2.4: Building a Deck
- •7.3: Tipping
- •Example 7.3.1: Tipping Versus Slipping
- •Example 7.3.2: Tipping While Pushing
- •7.4: Force Couples
- •Example 7.4.1: Rolling the Cylinder Over a Step
- •Homework for Week 7
- •Week 8: Fluids
- •Fluids Summary
- •8.1: General Fluid Properties
- •8.1.1: Pressure
- •8.1.2: Density
- •8.1.3: Compressibility
- •8.1.5: Properties Summary
- •Static Fluids
- •8.1.8: Variation of Pressure in Incompressible Fluids
- •Example 8.1.1: Barometers
- •Example 8.1.2: Variation of Oceanic Pressure with Depth
- •8.1.9: Variation of Pressure in Compressible Fluids
- •Example 8.1.3: Variation of Atmospheric Pressure with Height
- •Example 8.2.1: A Hydraulic Lift
- •8.3: Fluid Displacement and Buoyancy
- •Example 8.3.1: Testing the Crown I
- •Example 8.3.2: Testing the Crown II
- •8.4: Fluid Flow
- •8.4.1: Conservation of Flow
- •Example 8.4.1: Emptying the Iced Tea
- •8.4.3: Fluid Viscosity and Resistance
- •8.4.4: A Brief Note on Turbulence
- •8.5: The Human Circulatory System
- •Example 8.5.1: Atherosclerotic Plaque Partially Occludes a Blood Vessel
- •Example 8.5.2: Aneurisms
- •Homework for Week 8
- •Week 9: Oscillations
- •Oscillation Summary
- •9.1: The Simple Harmonic Oscillator
- •9.1.1: The Archetypical Simple Harmonic Oscillator: A Mass on a Spring
- •9.1.2: The Simple Harmonic Oscillator Solution
- •9.1.3: Plotting the Solution: Relations Involving
- •9.1.4: The Energy of a Mass on a Spring
- •9.2: The Pendulum
- •9.2.1: The Physical Pendulum
- •9.3: Damped Oscillation
- •9.3.1: Properties of the Damped Oscillator
- •Example 9.3.1: Car Shock Absorbers
- •9.4: Damped, Driven Oscillation: Resonance
- •9.4.1: Harmonic Driving Forces
- •9.4.2: Solution to Damped, Driven, Simple Harmonic Oscillator
- •9.5: Elastic Properties of Materials
- •9.5.1: Simple Models for Molecular Bonds
- •9.5.2: The Force Constant
- •9.5.3: A Microscopic Picture of a Solid
- •9.5.4: Shear Forces and the Shear Modulus
- •9.5.5: Deformation and Fracture
- •9.6: Human Bone
- •Example 9.6.1: Scaling of Bones with Animal Size
- •Homework for Week 9
- •Week 10: The Wave Equation
- •Wave Summary
- •10.1: Waves
- •10.2: Waves on a String
- •10.3: Solutions to the Wave Equation
- •10.3.1: An Important Property of Waves: Superposition
- •10.3.2: Arbitrary Waveforms Propagating to the Left or Right
- •10.3.3: Harmonic Waveforms Propagating to the Left or Right
- •10.3.4: Stationary Waves
- •10.5: Energy
- •Homework for Week 10
- •Week 11: Sound
- •Sound Summary
- •11.1: Sound Waves in a Fluid
- •11.2: Sound Wave Solutions
- •11.3: Sound Wave Intensity
- •11.3.1: Sound Displacement and Intensity In Terms of Pressure
- •11.3.2: Sound Pressure and Decibels
- •11.4: Doppler Shift
- •11.4.1: Moving Source
- •11.4.2: Moving Receiver
- •11.4.3: Moving Source and Moving Receiver
- •11.5: Standing Waves in Pipes
- •11.5.1: Pipe Closed at Both Ends
- •11.5.2: Pipe Closed at One End
- •11.5.3: Pipe Open at Both Ends
- •11.6: Beats
- •11.7: Interference and Sound Waves
- •Homework for Week 11
- •Week 12: Gravity
- •Gravity Summary
- •12.1: Cosmological Models
- •12.2.1: Ellipses and Conic Sections
- •12.4: The Gravitational Field
- •12.4.1: Spheres, Shells, General Mass Distributions
- •12.5: Gravitational Potential Energy
- •12.6: Energy Diagrams and Orbits
- •12.7: Escape Velocity, Escape Energy
- •Example 12.7.1: How to Cause an Extinction Event
- •Homework for Week 12

300 |
Week 6: Vector Torque and Angular Momentum |
distribution does not have mirror symmetry across the axis of rotation nor does it have mirror symmetry across the plane of rotation through the pivot. Like the unbalanced mass sweeping out a cone, the bearings have to exert a dynamically changing torque on the tires as they rotate because their angular momentum is not parallel to the axis of rotation. At the instant shown, the bearings are stressed in two places (to exert a net torque on the hub out of the page if the direction of ω~ is up as drawn).
The solution to the problem of tire imbalance is simple – rotate your tires (to maintain even wear) and have your tires regularly balanced by adding compensatory weights on the “light” side of a static imbalance and to restore relative cylindrical symmetry for dynamical imbalance, the way adding a second mass did to our single mass sweeping out a cone.
I should point out that there are other ways to balance a rotating rigid object, and that every rigid object, no matter how its mass is distributed, has at least certain axes through the center of mass that can “diagonalize” the moment of inertia with respect to those axes. These are the axes that you can spin the object about and it will rotate freely without any application of an outside force or torque. Sadly, though, this is beyond the scope of this course121
At this point you should understand how easy it is to evaluate the angular momentum of symmetric rotating rigid objects (given their moment of inertia) using L = Iω, and how very di cult it can be to manage the angular momentum in the cases where the mass distribution is asymmetric and unbalanced. In the latter case we will usually find that the angular momentum vector will precess around the axis of rotation, necessitating the application of a continuous torque to maintain the (somewhat “unnatural”) motion.
There is one other very important context where precession occurs, and that is when a symmetric rigid body is rapidly rotating and has a large angular momentum, and a torque is applied to it in just the right way. This is one of the most important problems we will learn to solve this week, one essential for everybody to know, future physicians, physicists, mathematicians, engineers: The Precession of a Top (or other symmetric rotator).
6.7: Precession of a Top
ωp
ω |
M |
R |
θ |
Mg |
D |
Figure 91:
Nowhere is the vector character of torque and angular momentum more clearly demonstrated than in the phenomenon of precession of a top, a spinning proton, or the Earth itself. This is also an
121Yes, I know, I know – this was a joke! I know that you aren’t, in fact, terribly sad about this...;-)
Week 6: Vector Torque and Angular Momentum |
301 |
important problem to clearly and quantitatively understand even in this introductory course because it is the basis of Magnetic Resonance Imaging (MRI) in medicine, the basis of understanding quantum phenomena ranging from spin resonance to resonant emission from two-level atoms for physicists, and the basis for gyroscopes to the engineer. Evvybody need to know it, in other words, no fair hiding behind the sputtered “but I don’t need to know this crap” weasel-squirm all too often uttered by frustrated students.
Look, I’ll bribe you. This is one of those topics/problems that I guarantee will be on at least one quiz, hour exam, or the final this semester. That is, mastering it will be worth at least ten points of your total credit, and in most years it is more likely to be thirty or even fifty points. It’s that important! If you master it now, then understanding the precession of a proton around a magnetic field will be a breeze next semester. Otherwise, you risk the additional 10-50 points it might be worth next semester.
If you are a sensible person, then, you will recognize that I’ve just made it worth your while to invest the time required to completely understand precession in terms of vector torque, and to be able to derive the angular frequency of precession, ωp – which is our goal. I’ll show you three ways to do it, don’t worry, and any of the three will be acceptable (although I prefer that you use the second or third as the first is a bit too simple, it gets the right answer but doesn’t give you a good feel for what happens if the forces that produce the torque change in time).
First, though, let’s understand the phenonenon. If figure ?? above, a simple top is shown spinning at some angular velocity ω (not to be confused with ωp, the precession frequency). We will idealize this particular top as a massive disk with mass M , radius R, spinning around a rigid massless spindle that is resting on the ground, tipped at an angle θ with respect to the vertical.
We begin by noting that this top is symmetric, so we can easily compute the magnitude and direction of its angular momentum:
~ |
1 |
2 |
|
|
|
|
|
|
|
||
L = |L| = Iω = |
|
2 |
M R |
ω |
(628) |
Using the “grasp the axis” version of the right hand rule, we see that in the example portrayed this angular momentum points in the direction from the pivot at the point of contact between the spindle and the ground and the center of mass of the disk along the axis of rotation.
Second, we note that there is a net torque exerted on the top relative to this spindle-ground contact point pivot due to gravity. There is no torque, of course, from the normal force that holds up the top, and we are assuming the spindle and ground are frictionless. This torque is a vector :
~ |
(629) |
~τ = D × (−M gzˆ) |
|
or |
|
τ = M gD sin(θ) |
(630) |
into the page as drawn above, where z is vertical.
Third we note that the torque will change the angular momentum by displacing it into the page
~
in the direction of the torque. But as it does so, the plane containing the D and M gzˆ will be rotated a tiny bit around the z (precession) axis, and the torque will also shift its direction to
~
remain perpendicular to this plane. It will shift L a bit more, which shifts ~τ a bit more and so on.
~
In the end L will precess around z, with ~τ precessing as well, always π/2 ahead .
~ |
~ |
~ |
Since ~τ L, the magnitude of L does not change, only the direction. |
L sweeps out a cone, |
|
exactly like the cone swept out in the unbalanced rotation problems above and we can use similar considerations to relate the magnitude of the torque (known above) to the change of angular momentum per period. This is the simplest (and least accurate) way to find the precession frequency. Let’s start by giving this a try:

302 Week 6: Vector Torque and Angular Momentum
Example 6.7.1: Finding ωp From L/ T (Average)
We already derived above that |
|
τavg = τ = M gD sin(θ) |
(631) |
is the magnitude of the torque at all points in the precession cycle, and hence is also the average of the magnitude of the torque over a precession cycle (as opposed to the average of the vector torque over a cycle, which is obviously zero).
We now compute the average torque algebraically from L/ t (average) and set it equal to the computed torque above. That is:
Lcycle = 2πL = 2πL sin(θ)
and:
2π
tcycle = T = ωp
where ωp is the (desired) precession frequency, or: |
|
|
τavg = M gD sin(θ) = |
Lcycle |
= ωpL sin(θ) |
|
||
|
tcycle |
|
We now solve the the precession frequency ωp:
ωp = |
M gD |
= |
M gD |
= |
2gD |
|
|
|
|||
L |
Iω |
R2ω |
(632)
(633)
(634)
(635)
Note well that the precession frequencey is independent of θ – this is extremely important next semester when you study the precession of spinning charged particles around an applied magnetic field, the basis of Magnetic Resonance Imaging (MRI).
Example 6.7.2: Finding ωp from L and T Separately
Simple and accurate as it is, the previous derivation has a few “issues” and hence it is not my favorite one; averaging in this way doesn’t give you the most insight into what’s going on and doesn’t help you get a good feel for the calculus of it all. This matters in MRI, where the magnetic field varies in time, although it is a bit more di cult to make gravity vary in a similar way so it doesn’t matter so much this semester.
Nevertheless, to get you o on the right foot, so to speak, for E&M122, let’s do a second derivation that is in between the very crude averaging up above and a rigorous application of calculus to the problem that we can’t even understand properly until we reach the week where we cover oscillation.
Let’s repeat the general idea of the previous derivation, only instead of setting τ equal to the
~ ~
average change in L per unit time, we will set it equal to the instantaneous change in L per unit time, writing everything in terms of very small (but finite) intervals and then taking the appropriate limits.
~
To do this, we need to picture how L changes in time. Note well that at any given instant, ~τ
~
is perpendicular to the plane containing −yˆ (the direction of the gravitational force) and L. This
~ |
|
|
direction is thus always perpendicular to both L and −M gzˆ and cannot change the magnitude |
||
~ |
~ |
~ |
of L or its z component Lz . Over a very short time |
t, the change in L is thus |
L in the |
plane perpendicular to zˆ. As the angular momentum changes direction only into the ~τ direction, the ~τ direction also changes to remain perpendicular. This should remind you have our long-ago
122Electricity and Magnetism
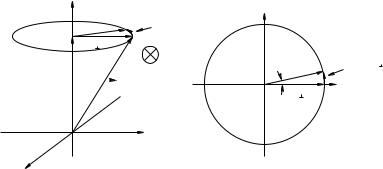
Week 6: Vector Torque and Angular Momentum |
303 |
z |
|
|
y |
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
L |
τ in |
|
|
|
|
|
Δφ |
L = L Δφ = τ |
t |
|
|
|
|
|||
Lz |
L |
|
L |
x |
|
|
|
|
|||
|
θ |
|
|
|
|
|
|
y |
|
|
|
x
|
~ |
Figure 92: The cone swept out by the precession of the angular momentum vector, L, as well as an |
|
~ |
~ |
“overhead view” of the trajectory of L , the component of L perpendicular to the z-axis.
~
discussion of the kinematics of circular motion – L sweeps out a cone around the z-axis where Lz and the magnitude of L remain constant.
L |
|
sweeps out a circle as we saw in the previous example, and we can visualize both the cone |
||||||||||||
|
~ |
|
|
|
|
|
t, |
~ |
|
|
|
|
|
|
swept out by L and the change over a short time |
|
L, in figure 92. We can see from the figure |
||||||||||||
that: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L = L |
φ = τ t |
|
|
|
(636) |
|||||
where φ is the angle the angular momentum vector precesses through in time |
t. We substitute |
|||||||||||||
L = L sin(θ) and τ = M gD sin(θ) as before, and get: |
|
|
|
|
|
|
||||||||
|
|
L sin(θ) |
φ = M gD sin(θ) |
t |
(637) |
|||||||||
Finally we solve for: |
|
|
|
|
|
|
|
|
|
|
||||
|
|
ωp = |
dφ |
= |
lim |
|
φ |
= |
M gD |
= |
|
2gD |
|
(638) |
|
|
|
|
|
|
|
R2ω |
|||||||
|
|
|
dt |
t→0 |
φ |
L |
|
|
||||||
as before. Note well that because this time we could take the limit as t → 0, we get an expression that is good at any instant in time, even if the top is in a rocket ship (an accelerating frame) and g → g′ is varying in time!
This still isn’t the most elegant approach. The best approach, although it does use some real calculus, is to just write down the equation of motion for the system as di erential equations and
~
solve them for both L(t) and for ωp.
Example 6.7.3: Finding ωp from Calculus
Way back at the beginning of this section we wrote down Newton’s Second Law for the rotation of the gyroscope directly:
|
|
|
|
|
|
~ |
|
|
|
|
|
|
(639) |
|
|
|
|
|
~τ = D × (−M gzˆ) |
|
|
|
|
||||
Because −M gzˆ points only in the negative z-direction and |
|
|
|
||||||||||
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
~ |
L |
|
|
|
|
|
|
|
|
|
|
|
|
D = D |
L |
|
|
|
|
|
(640) |
~ |
~ |
|
|
|
~ |
|
|
|
|
|
|
|
|
because L is parallel to D, for a general L = Lxxˆ + Ly yˆ we get precisely two terms out of the cross |
|||||||||||||
product: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dLx |
|
= τx |
= |
M gD sin(θ) = |
M gDLy |
(641) |
|||||
|
|
dt |
|
|
L |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
dLy |
|
= τy |
= |
−M gD sin(θ) |
= − |
M gDLx |
(642) |
||||
|
|
dt |
|
L |
|||||||||
304 |
|
|
Week 6: Vector Torque and Angular Momentum |
|||
or |
|
|
|
|
|
|
dLx |
= |
|
M gD |
Ly |
(643) |
|
|
dt |
|
||||
|
|
|
L |
|
||
|
dLy |
= |
|
M gD |
Lx |
(644) |
|
dt |
|
|
|||
|
|
|
L |
|
||
If we di erentiate the first expression and substitute the second into the first (and vice versa) we transform this pair of coupled first order di erential equations for Lx and Ly into the following pair of second order di erential equations:
dt2 |
= |
µ |
L |
¶ |
Lx |
= |
ωp2Lx |
(645) |
d2Lx |
|
|
M gD |
|
2 |
|
|
|
dt2 |
= |
µ |
L |
¶ |
Ly |
= |
ωp2Ly |
(646) |
d2Ly |
|
|
M gD |
|
2 |
|
|
|
|
|
|
|
|
|
|
These (either one) we will learn to recognize as the di erential equation of motion for the simple harmonic oscillator. A particular solution of interest (that satisfies the first order equations above) might be:
Lx(t) = |
Lx0 cos(ωpt) |
(647) |
|
Lx(t) |
= |
Lx0 sin(ωpt) |
(648) |
Lz (t) |
= |
Lz0 |
(649) |
~
which is then the exact solution to the equation of motion for L(t) that describes the actual cone being swept out, with no hand-waving or limit taking required.
The only catch to this approach is, of course, that we don’t know how to solve the equation of motion yet, and the very phrase “second order di erential equation” strikes terror into our hearts in spite of the fact that we’ve been solving one after another since week 1 in this class! All of the equations of motion we have solved from Newton’s Second Law have been second order ones, after all – it is just that the ones for constant acceleration were directly integrable where this set is not, at least not easily.
It is pretty easy to solve for all of that, but we will postpone the actual solution until later. In the meantime, remember, you must know how to reproduce one of the three derivations above for ωp, the angular precession frequency, for at least one quiz, test, or hour exam. Not to mention a homework problem, below. Be sure that you master this because precession is important.
One last suggestion before we move on to treat angular collisions. Most students have a lot of experience with pushes and pulls, and so far it has been pretty easy to come up with everyday experiences of force, energy, one dimensional torque and rolling, circular motion, and all that. It’s not so easy to come up with everyday experiences involving vector torque and precession. Yes, may of you played with tops when you were kids, yes, nearly everybody rode bicycles and balancing and steering a bike involves torque, but you haven’t really felt it knowing what was going on.
The only device likely to help you to personally experience torque “with your own two hands” is the bicycle wheel with handles and the string that was demonstrated in class. I urge you to take a turn spinning this wheel and trying to turn it by means of its handles while it is spinning, to spin it and suspend it by the rope attached to one handle and watch it precess. Get to where you can predict the direction of precession given the direction of the spin and the handle the rope is attached to, get so you have experience of pulling it (say) in and out and feeling the handles deflect up and down or vice versa. Only thus can you feel the nasty old cross product in both the torque and the angular momentum, and only thus can you come to understand torque with your gut as well as your head.
