
- •Preface
- •Textbook Layout and Design
- •Preliminaries
- •See, Do, Teach
- •Other Conditions for Learning
- •Your Brain and Learning
- •The Method of Three Passes
- •Mathematics
- •Summary
- •Homework for Week 0
- •Summary
- •1.1: Introduction: A Bit of History and Philosophy
- •1.2: Dynamics
- •1.3: Coordinates
- •1.5: Forces
- •1.5.1: The Forces of Nature
- •1.5.2: Force Rules
- •Example 1.6.1: Spring and Mass in Static Force Equilibrium
- •1.7: Simple Motion in One Dimension
- •Example 1.7.1: A Mass Falling from Height H
- •Example 1.7.2: A Constant Force in One Dimension
- •1.7.1: Solving Problems with More Than One Object
- •Example 1.7.4: Braking for Bikes, or Just Breaking Bikes?
- •1.8: Motion in Two Dimensions
- •Example 1.8.1: Trajectory of a Cannonball
- •1.8.2: The Inclined Plane
- •Example 1.8.2: The Inclined Plane
- •1.9: Circular Motion
- •1.9.1: Tangential Velocity
- •1.9.2: Centripetal Acceleration
- •Example 1.9.1: Ball on a String
- •Example 1.9.2: Tether Ball/Conic Pendulum
- •1.9.3: Tangential Acceleration
- •Homework for Week 1
- •Summary
- •2.1: Friction
- •Example 2.1.1: Inclined Plane of Length L with Friction
- •Example 2.1.3: Find The Minimum No-Skid Braking Distance for a Car
- •Example 2.1.4: Car Rounding a Banked Curve with Friction
- •2.2: Drag Forces
- •2.2.1: Stokes, or Laminar Drag
- •2.2.2: Rayleigh, or Turbulent Drag
- •2.2.3: Terminal velocity
- •Example 2.2.1: Falling From a Plane and Surviving
- •2.2.4: Advanced: Solution to Equations of Motion for Turbulent Drag
- •Example 2.2.3: Dropping the Ram
- •2.3.1: Time
- •2.3.2: Space
- •2.4.1: Identifying Inertial Frames
- •Example 2.4.1: Weight in an Elevator
- •Example 2.4.2: Pendulum in a Boxcar
- •2.4.2: Advanced: General Relativity and Accelerating Frames
- •2.5: Just For Fun: Hurricanes
- •Homework for Week 2
- •Week 3: Work and Energy
- •Summary
- •3.1: Work and Kinetic Energy
- •3.1.1: Units of Work and Energy
- •3.1.2: Kinetic Energy
- •3.2: The Work-Kinetic Energy Theorem
- •3.2.1: Derivation I: Rectangle Approximation Summation
- •3.2.2: Derivation II: Calculus-y (Chain Rule) Derivation
- •Example 3.2.1: Pulling a Block
- •Example 3.2.2: Range of a Spring Gun
- •3.3: Conservative Forces: Potential Energy
- •3.3.1: Force from Potential Energy
- •3.3.2: Potential Energy Function for Near-Earth Gravity
- •3.3.3: Springs
- •3.4: Conservation of Mechanical Energy
- •3.4.1: Force, Potential Energy, and Total Mechanical Energy
- •Example 3.4.1: Falling Ball Reprise
- •Example 3.4.2: Block Sliding Down Frictionless Incline Reprise
- •Example 3.4.3: A Simple Pendulum
- •Example 3.4.4: Looping the Loop
- •3.5: Generalized Work-Mechanical Energy Theorem
- •Example 3.5.1: Block Sliding Down a Rough Incline
- •Example 3.5.2: A Spring and Rough Incline
- •3.5.1: Heat and Conservation of Energy
- •3.6: Power
- •Example 3.6.1: Rocket Power
- •3.7: Equilibrium
- •3.7.1: Energy Diagrams: Turning Points and Forbidden Regions
- •Homework for Week 3
- •Summary
- •4.1: Systems of Particles
- •Example 4.1.1: Center of Mass of a Few Discrete Particles
- •4.1.2: Coarse Graining: Continuous Mass Distributions
- •Example 4.1.2: Center of Mass of a Continuous Rod
- •Example 4.1.3: Center of mass of a circular wedge
- •4.2: Momentum
- •4.2.1: The Law of Conservation of Momentum
- •4.3: Impulse
- •Example 4.3.1: Average Force Driving a Golf Ball
- •Example 4.3.2: Force, Impulse and Momentum for Windshield and Bug
- •4.3.1: The Impulse Approximation
- •4.3.2: Impulse, Fluids, and Pressure
- •4.4: Center of Mass Reference Frame
- •4.5: Collisions
- •4.5.1: Momentum Conservation in the Impulse Approximation
- •4.5.2: Elastic Collisions
- •4.5.3: Fully Inelastic Collisions
- •4.5.4: Partially Inelastic Collisions
- •4.6: 1-D Elastic Collisions
- •4.6.1: The Relative Velocity Approach
- •4.6.2: 1D Elastic Collision in the Center of Mass Frame
- •4.7: Elastic Collisions in 2-3 Dimensions
- •4.8: Inelastic Collisions
- •Example 4.8.1: One-dimensional Fully Inelastic Collision (only)
- •Example 4.8.2: Ballistic Pendulum
- •Example 4.8.3: Partially Inelastic Collision
- •4.9: Kinetic Energy in the CM Frame
- •Homework for Week 4
- •Summary
- •5.1: Rotational Coordinates in One Dimension
- •5.2.1: The r-dependence of Torque
- •5.2.2: Summing the Moment of Inertia
- •5.3: The Moment of Inertia
- •Example 5.3.1: The Moment of Inertia of a Rod Pivoted at One End
- •5.3.1: Moment of Inertia of a General Rigid Body
- •Example 5.3.2: Moment of Inertia of a Ring
- •Example 5.3.3: Moment of Inertia of a Disk
- •5.3.2: Table of Useful Moments of Inertia
- •5.4: Torque as a Cross Product
- •Example 5.4.1: Rolling the Spool
- •5.5: Torque and the Center of Gravity
- •Example 5.5.1: The Angular Acceleration of a Hanging Rod
- •Example 5.6.1: A Disk Rolling Down an Incline
- •5.7: Rotational Work and Energy
- •5.7.1: Work Done on a Rigid Object
- •5.7.2: The Rolling Constraint and Work
- •Example 5.7.2: Unrolling Spool
- •Example 5.7.3: A Rolling Ball Loops-the-Loop
- •5.8: The Parallel Axis Theorem
- •Example 5.8.1: Moon Around Earth, Earth Around Sun
- •Example 5.8.2: Moment of Inertia of a Hoop Pivoted on One Side
- •5.9: Perpendicular Axis Theorem
- •Example 5.9.1: Moment of Inertia of Hoop for Planar Axis
- •Homework for Week 5
- •Summary
- •6.1: Vector Torque
- •6.2: Total Torque
- •6.2.1: The Law of Conservation of Angular Momentum
- •Example 6.3.1: Angular Momentum of a Point Mass Moving in a Circle
- •Example 6.3.2: Angular Momentum of a Rod Swinging in a Circle
- •Example 6.3.3: Angular Momentum of a Rotating Disk
- •Example 6.3.4: Angular Momentum of Rod Sweeping out Cone
- •6.4: Angular Momentum Conservation
- •Example 6.4.1: The Spinning Professor
- •6.4.1: Radial Forces and Angular Momentum Conservation
- •Example 6.4.2: Mass Orbits On a String
- •6.5: Collisions
- •Example 6.5.1: Fully Inelastic Collision of Ball of Putty with a Free Rod
- •Example 6.5.2: Fully Inelastic Collision of Ball of Putty with Pivoted Rod
- •6.5.1: More General Collisions
- •Example 6.6.1: Rotating Your Tires
- •6.7: Precession of a Top
- •Homework for Week 6
- •Week 7: Statics
- •Statics Summary
- •7.1: Conditions for Static Equilibrium
- •7.2: Static Equilibrium Problems
- •Example 7.2.1: Balancing a See-Saw
- •Example 7.2.2: Two Saw Horses
- •Example 7.2.3: Hanging a Tavern Sign
- •7.2.1: Equilibrium with a Vector Torque
- •Example 7.2.4: Building a Deck
- •7.3: Tipping
- •Example 7.3.1: Tipping Versus Slipping
- •Example 7.3.2: Tipping While Pushing
- •7.4: Force Couples
- •Example 7.4.1: Rolling the Cylinder Over a Step
- •Homework for Week 7
- •Week 8: Fluids
- •Fluids Summary
- •8.1: General Fluid Properties
- •8.1.1: Pressure
- •8.1.2: Density
- •8.1.3: Compressibility
- •8.1.5: Properties Summary
- •Static Fluids
- •8.1.8: Variation of Pressure in Incompressible Fluids
- •Example 8.1.1: Barometers
- •Example 8.1.2: Variation of Oceanic Pressure with Depth
- •8.1.9: Variation of Pressure in Compressible Fluids
- •Example 8.1.3: Variation of Atmospheric Pressure with Height
- •Example 8.2.1: A Hydraulic Lift
- •8.3: Fluid Displacement and Buoyancy
- •Example 8.3.1: Testing the Crown I
- •Example 8.3.2: Testing the Crown II
- •8.4: Fluid Flow
- •8.4.1: Conservation of Flow
- •Example 8.4.1: Emptying the Iced Tea
- •8.4.3: Fluid Viscosity and Resistance
- •8.4.4: A Brief Note on Turbulence
- •8.5: The Human Circulatory System
- •Example 8.5.1: Atherosclerotic Plaque Partially Occludes a Blood Vessel
- •Example 8.5.2: Aneurisms
- •Homework for Week 8
- •Week 9: Oscillations
- •Oscillation Summary
- •9.1: The Simple Harmonic Oscillator
- •9.1.1: The Archetypical Simple Harmonic Oscillator: A Mass on a Spring
- •9.1.2: The Simple Harmonic Oscillator Solution
- •9.1.3: Plotting the Solution: Relations Involving
- •9.1.4: The Energy of a Mass on a Spring
- •9.2: The Pendulum
- •9.2.1: The Physical Pendulum
- •9.3: Damped Oscillation
- •9.3.1: Properties of the Damped Oscillator
- •Example 9.3.1: Car Shock Absorbers
- •9.4: Damped, Driven Oscillation: Resonance
- •9.4.1: Harmonic Driving Forces
- •9.4.2: Solution to Damped, Driven, Simple Harmonic Oscillator
- •9.5: Elastic Properties of Materials
- •9.5.1: Simple Models for Molecular Bonds
- •9.5.2: The Force Constant
- •9.5.3: A Microscopic Picture of a Solid
- •9.5.4: Shear Forces and the Shear Modulus
- •9.5.5: Deformation and Fracture
- •9.6: Human Bone
- •Example 9.6.1: Scaling of Bones with Animal Size
- •Homework for Week 9
- •Week 10: The Wave Equation
- •Wave Summary
- •10.1: Waves
- •10.2: Waves on a String
- •10.3: Solutions to the Wave Equation
- •10.3.1: An Important Property of Waves: Superposition
- •10.3.2: Arbitrary Waveforms Propagating to the Left or Right
- •10.3.3: Harmonic Waveforms Propagating to the Left or Right
- •10.3.4: Stationary Waves
- •10.5: Energy
- •Homework for Week 10
- •Week 11: Sound
- •Sound Summary
- •11.1: Sound Waves in a Fluid
- •11.2: Sound Wave Solutions
- •11.3: Sound Wave Intensity
- •11.3.1: Sound Displacement and Intensity In Terms of Pressure
- •11.3.2: Sound Pressure and Decibels
- •11.4: Doppler Shift
- •11.4.1: Moving Source
- •11.4.2: Moving Receiver
- •11.4.3: Moving Source and Moving Receiver
- •11.5: Standing Waves in Pipes
- •11.5.1: Pipe Closed at Both Ends
- •11.5.2: Pipe Closed at One End
- •11.5.3: Pipe Open at Both Ends
- •11.6: Beats
- •11.7: Interference and Sound Waves
- •Homework for Week 11
- •Week 12: Gravity
- •Gravity Summary
- •12.1: Cosmological Models
- •12.2.1: Ellipses and Conic Sections
- •12.4: The Gravitational Field
- •12.4.1: Spheres, Shells, General Mass Distributions
- •12.5: Gravitational Potential Energy
- •12.6: Energy Diagrams and Orbits
- •12.7: Escape Velocity, Escape Energy
- •Example 12.7.1: How to Cause an Extinction Event
- •Homework for Week 12

294 |
Week 6: Vector Torque and Angular Momentum |
this point in the course you have no doubt gotten much better at math and have started to overcome your fears – there is no need to charge you points for wading through stu I could make a mistake doing almost as easily as you could. If anything, we’ll give you extra points if you try it and succeed
– after giving us something clear and correct to grade for primary credit first!
Finally, we do need to compute the kinetic energy lost in the collision:
K = Kf − Ki = |
Lf2 |
+ |
1 |
(m + M )vf2 − |
1 |
mv02 |
(608) |
2If |
2 |
2 |
is as easy a form as any. Here there may be some point to squaring everything out to simplify, as one expects an answer that should be “some fraction of Ki”, and the value of the fraction might be interesting. Again, if you are a physics major you should probably do the full simplification just for practice doing lots of tedious algebra without fear, useful self-discipline. Everybody else that does it will likely get extra credit unless the problem explicitly calls for it.
Now, let’s do the whole thing over, using a di erent pivot, and see where things are the same and where they are di erent.
Using the end of the rod:
Obviously there is no change in the computation of xcm and vf – indeed, we really did these in the (given) coordinate frame starting at the end of the rod anyway – that’s the “lab” frame drawn into our figure and the one wherein our answer is finally expressed. All we need to do, then, is compute our angular momenta relative to an origin/pivot at the end of the rod:
Li = |~r × p~| = r mv0 = mv0L |
(609) |
and: |
|
Lf = (m + M )vf xcm + If ωf |
(610) |
In this final expression, (m + M )vf xcm is the angular momentum of the entire system treated as a mass moving at speed vf located at xcm right after the collision, plus the angular momentum of the system around the center of mass, which must be computed exactly as before, same If , same ωf (to be found). Thus:
If ωf = mv0L − (m + M )vf xcm |
(611) |
Here is a case where one really must do a bit more simplification – there are just too many things that depend on the initial conditions. If we substitute in vf from above, in particular, we get:
|
If ωf = mv0L − mv0xcm = mv0(L − xcm) |
(612) |
||||
and: |
mv0(L − xcm) |
|
|
|
mv0(L − xcm) |
|
ωf = |
= |
|
1 |
(613) |
||
|
|
M L2 + M (xcm − L/2)2 + m(L − xcm)2 |
||||
|
If |
|
|
|||
|
|
12 |
|
|||
as before. The algebra somehow manages the frame change for us, giving us an answer that doesn’t depend on the particular choice of frame once we account for the angular momentum of the center of mass in any frame with a pivot that isn’t on the line of motion of xcm (where it is zero). Obviously, computing K is the same, and so we are done!. Same answer, two di erent frames!
Example 6.5.2: Fully Inelastic Collision of Ball of Putty with Pivoted Rod
In figure 87 we see the alternative version of the fully inelastic collision between a pivoted rod and a blob of putty. Let us consider the answers to the questions in the previous problem. Some of them will either be exactly the same or in some sense “irrelevant” in the case of a pivoted rod, but either way we need to understand that.

Week 6: Vector Torque and Angular Momentum |
295 |
pivot
M
M L
ω f
 m
m
m v0
Figure 87: A blob of putty of mass m travelling at speed v0 strikes the rod of mass M and length L at the end and sticks. The rod, however, is pivoted about the other end on a frictionless nail or hinge.
First, however, the physics! Without the physics we wither and die! There is a pivot, and during the collision the pivot exerts a large and unknown pivot force on the rod120 and this force cannot be ignored in the impulse approximation. Consequently, linear momentum is not conserved!
It is obviously an inelastic collision, so kinetic energy is not conserved.
The force exerted by the physical hinge or nail may be unknown and large, but if we make the hinge the pivot for the purposes of computing torque and angular momentum, this force exerts no torque on the system! Consequently, for this choice of pivot only, angular momentum is conserved.
In a sense, this makes this problem much simpler than the last one! We have only one physical principle to work with (plus our definitions of e.g. center of mass), and all of the other answers must be derivable from this one thing. So we might as well get to work:
Li = I0ω0 = mL |
2 v0 |
|
1 |
2 |
2 |
|
|
|
|
= ( |
|
M L + mL )ωf = If ωf = Lf |
(614) |
||
|
L |
3 |
|||||
where I used Lf = If ωf and inserted the scalar moment of inertial If by inspection, as I know the moment of inertia of a rod about its end as well as the moment of inertia of a point mass a distance L from the pivot axis. Thus:
ωf = |
mv0L |
= |
|
m v0 |
= |
|
m |
ω0 |
(615) |
||
|
|
|
|
|
|
|
|||||
( 31 M + m)L2 |
( 13 M + m) L |
( 13 M + m) |
|||||||||
where I’ve written it in the latter form (in terms of the initial angular velocity of the blob of putty relative to this pivot) both to make the correctness of the units manifest and to illustrate how conceptually simple the answer is:
ωf = |
I0 |
ω0 |
(616) |
|
|||
|
If |
|
|
It is now straightforward to answer any other questions that might be asked. The center of mass is still a distance:
|
m + 1 M |
|
|
xcm = |
2 |
L |
(617) |
m + M |
120Unless the mass strikes the rod at a particular point called the center of percussion of the rod, such that the
velocity of the center of mass right after the collision is exactly the same as that of the free rod found above...
296 |
Week 6: Vector Torque and Angular Momentum |
from the pivot, but now it moves in a circular arc after the collision, not in a straight line.
The velocity of the center of mass after the collision is determined from ωf :
|
m v0 |
× |
m + 21 M |
|
L = |
m(m + 21 M ) |
||||||||
vf = ωf xcm = |
|
|
|
|
|
|
|
|
|
v0 |
||||
( 13 M + m) L |
|
m + M |
(m + M )( 31 M + m) |
|||||||||||
The kinetic energy lost in the collision is: |
|
|
|
|
|
|
|
|
|
|
||||
|
K = Kf − Ki = |
Lf2 |
|
− |
1 |
mv02 |
||||||||
|
2If |
|
2 |
|||||||||||
(618)
(619)
(which can be simplified, but the simplification is left as an exercise for everybody – it isn’t di cult). One can even compute the impulse provided by the pivot hinge during the collision:
Ihinge = p = pf − pi = (m + M )vf − mv0 |
(620) |
using vf from above. (Note well that I have to reuse symbols such as I, in the same problem sorry
– in this context it clearly means “impulse” and not “moment of inertia”.)
6.5.1: More General Collisions
As you can imagine, problems can get to be somewhat more di cult than the previous two examples in several ways. For one, instead of collisions between point masses that stick and rods (pivoted or not) one can have collisions between point masses and rods where the masses do not stick. This doesn’t change the basic physics. Either the problem will specify that the collision is elastic (so Ktot is conserved) or it will specify something like vf for the point mass so that you can compute
K and possibly p or L (depending on what is conserved), much as you did for bullet-passes- through-block problems in week 4.
Instead of point mass and rod at all you could be given a point mass and a disk or ball that can rotate, or even a collision between two disks. The algebra of things like this will be identical to the algebra above except that one will have to substitute e.g. the moment of inertia of a disk, or ball, or whatever for the moment of inertia of the rod, pivoted or free. The general method of solution will therefore be the same. You have several homework problems where you can work through this method on your own and working in your groups – make sure that you are comfortable with this before the quiz.
Angular momentum isn’t just conserved in the case of symmetric objects rotating, but these are by far the easiest for us to treat. We now need to tackle the various di culties associated with the rotation of asymmetric rigid objects, and then move on to finally and irrevocably understand how torque and angular momentum are vector quantities and that this matters.
6.6: Angular Momentum of an Asymmetric Rotating Rigid
Object
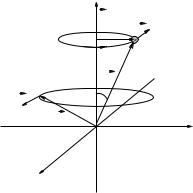
Consider the single particle in figure 88 that moves in a simple circle of radius r sin(θ) in a plane above the x-y plane! The axis of rotation of the particle (the “direction of the rotation” we considered in week 5 is clearly ω~ = ωzˆ.
Note well that the mass distribution of this rigid object rotation violates both of the symmetry rules above. It is not symmetric across the axis of rotation, nor is it symmetric across the plane of rotation. Consequently, according to our fundamental definition of the vector angular momentum:
~ |
(621) |
L = ~r × p~ = ~r × m~v |
Week 6: Vector Torque and Angular Momentum |
297 |
z
ω
v
m |
|
r |
τ |
θ |
|
|
|
L |
|
y |
|
x |
Figure 88: A point mass m at the end of a massless rod that makes a vector ~r from the origin to the location of the mass, moving at constant speed v sweeps out a circular path of radius r sin(θ) in a plane above the (point) pivot. The angular momentum of this mass is (at the instant shown)
~ |
~ |
L = ~r×m~v = ~r×p~ as shown. As the particle sweeps out a circle, so does L! The extended massless |
|
rigid rod exerts a constantly changing/precessing torque ~τ |
on the mass in order to accomplish this. |
which points up and to the left at the instant shown in figure 88.
~ |
|
|
Note well that L is perpendicular to both the plane containing ~r and ~v, and that as the mass |
||
~ |
~ |
|
moves around in a circle, so does L! In fact the vector L sweeps out a cone, just as the vector |
||
|
~ |
|
~r does. Finally, note that the magnitude of L has the constant value: |
|
|
|
L = |~r × ~v| = mvr |
(622) |
because ~r and ~v are mutually perpendicular.
~ ~
This means, of course, that although L = |L| is constant, L is constantly changing in time. Also,
~
we know that the time rate of change of L is ~τ, so the rod must be exerting a nonzero torque on the mass! Finally, the scalar moment of inertia I = Izz = mr2 sin2(θ) for this rotation is a constant
~
(and so is ω~) – manifestly L 6= Iω~! They don’t even point in the same direction!
Consider the following physics. We know that the actual magnitude and direction the force acting on m at the instant drawn is precisely Fc = mv2/(r sin(θ) (in towards the axis of rotation) because the mass m is moving in a circle. This force must be exerted by the massless rod because there is nothing else touching the mass (and we are neglecting gravity, drag, and all that). In turn, this force must be transmitted by the rod back to a bearing of some sort located at the origin, that keeps the rod from twisting out to rotate the mass in the same plane as the pivot (it’s “natural” state of rigid rotation).
The rod exerts a torque on the mass of magnitude:
~ |
2 cos(θ) |
2 |
|
2 |
|
|
|
τrod = |~r × F c| = r cos(θ)Fc = mv |
|
sin(θ) |
= mω |
r |
|
sin(θ) cos(θ) |
(623) |
Now, let’s see how this compares to the total change in angular momentum per unit time. Note
~
that the magnitude of L, L, does not change in time, nor does Lz , the component parallel to the z-axis. Only the component in the x-y plane changes, and that components sweeps out a circle!
The radius of the circle is L = L cos(θ) (from examining the various right triangles in the figure)
~
and hence the total change in L in one revolution is:
L = 2πL = 2πL cos(θ) |
(624) |
This change occurs in a time interval t = T , the period of rotation of the mass m. The period of
298 |
Week 6: Vector Torque and Angular Momentum |
rotation of m is the distance it travels (circumference of the circle of motion) divided by its speed:
|
|
|
|
T = |
2πr sin(θ) |
|
|
(625) |
||
|
|
|
|
v |
|
|||||
|
|
|
|
|
|
|
|
|||
Thus the magnitude of the torque exerted over t = T is (using L = mvr as well): |
|
|||||||||
|
L |
= 2πL cos(θ) |
v |
= mv2 |
cos(θ) |
= mω2r2 sin(θ) cos(θ) |
(626) |
|||
|
t |
|
2πr sin(θ) |
sin(θ) |
||||||
|
|
|
|
|
|
|||||
so that indeed,
~τrod = |
L |
|
|
(627) |
|
|
||
|
t |
|
for the cycle of motion.
The rod must indeed exert a constantly changing torque on the rod, a torque that remains perpendicular to the angular momentum vector at all times. The particle itself, the angular momentum, and the torque acting on the angular momentum all precess around the z-axis with a
~
period of revolution of T and clearly at no time is it true that L = Iω~ for any scalar I and constant
ω~.
|
|
z |
|
|
|
ω |
|
z |
|
v |
|
ω |
v |
m |
|
m |
|
||
m |
L tot |
||
v |
|||
|
|
r |
|
Ltot |
r |
|
|
r |
L |
||
|
L |
||
|
L |
y |
|
L |
|
||
|
y |
r |
|
|
x |
||
|
|
||
x |
|
v |
|
|
|
||
|
|
m |
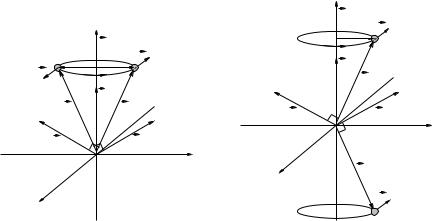
Figure 89: When the two masses have mirror symmetry across the axis of rotation, their
~
total angular momentum L does line up with ω~. When the two masses have mirror symmetry
~
across the plane of rotation, their total angular momentum L also lines up with ω~.
Notice how things change if we balance the mass with a second one on an opposing rod as drawn in figure 89, making the distribution mirror symmetric across the axis of rotation. Now each of the two masses has a torque acting on it due to the rod connecting it with the origin, each mass
~
has a vector angular momentum that at right angles to both ~r and ~v, but the components of L in the x-y plane phcancel so that the total angular momentum once again lines up with the z-axis!
The same thing happens if we add a second mass at the mirror-symmetric position below the plane of rotation as shown in the second panel of figure 89. In this case as well the components of
~
L in the x-y plane cancel while the z components add, producing a total vector angular momentum that points in the z-direction, parallel to ω~.
The two ways of balancing a mass point around a pivot are not quite equivalent. In the first case, the pivot axis passes through the center of mass of the system, and the rotation can be maintained without any external force as well as torque. In the second case, however, the center of mass of the system itself is moving in a circle (in the plane of rotation). Consequently, while no net external torque is required to maintain the motion, there is a net external force required to maintain the motion. We will di erentiate between these two cases below in an everyday example where they matter.
