That’s it. Really, pretty simple.

Needless to say, the idea of stable versus unstable and neutral equilibrium still holds for torques as well as forces. We will consider an equilibrium to be stable only if both the force and the torque are “restoring” – and push or twist the system back to the equilibrium if we make small linear or angular displacements away from it.

7.2: Static Equilibrium Problems

After working so long and hard on solving actual dynamical problems involving force and torque, static equilibrium problems sound like they would be pretty trivial. After all, nothing happens! It seems as though solving for what happens when nothing happens would be easy.

Not so. To put it in perspective, let’s consider why we might want to solve a problem in static equilibrium. Suppose we want to build a house. A properly built house is one that won’t just fall down, either all by itself or the first time the wolf hu s and pu s at your door. It seems as though building a house that is stable enough not to fall down when you move around in it, or load it with furniture in di erent ways, or the first time a category 2 hurricane roars by overhead and whacks it with 160 kilometer per hour winds is a worthy design goal. You might even want it to survive earthquakes!

If you think that building a stable house is easy, I commend trying to build a house out of cards125 . You will soon learn that balancing force loads, taking advantage of friction (or other “fastening” forces”, avoiding unbalanced torques is all actually remarkably tricky, for all that we can learn to do it without solving actual equations. Engineers who want to build serious structures such as bridges, skyscrapers, radio towers, cars, airplanes, and so on spend a lot of time learning statics (and a certain amount of dynamics, because no structure in a dynamical world filled with Big Bad Wolves is truly “static”) because it is very expensive when buildings, bridges, and so on fall down, when their structural integrity fails.

Stability is just as important for physicians to understand. The human body is not the world’s most stable structure, as it turns out. If you have ever played with Barbie or G.I. Joe dolls, then you understand that getting them to stand up on their own takes a bit of doing – just a bit of bend at the waist, just a bit too much weight at the side, or the feet not adjusted just so, and they fall right over. Actual humans stabilize their erect stance by constantly adjusting the force balance of their feet, shifting weight without thinking to the heel or to the toes, from the left foot to the right foot as they move their arms or bend at the waist or lift something. Even healthy, coordinated adults who are paying attention nevertheless sometimes lose their balance because their motions exceed the fairly narrow tolerance for stability in some stance or another.

This ability to remain stable standing up or walking rapidly disappears as one’s various sensory feedback mechanisms are impaired, and many, many health conditions impair them. Drugs or alcohol, neuropathy, disorders of the vestibular system, pain and weakness due to arthritis or aging. Many injuries (especially in the elderly) occur because people just plain fall over.

Then there is the fact that nearly all of our physical activity involves the adjustment of static balance between muscles (providing tension) and bones (providing compression), with our joints becoming stress-points that have to provide enormous forces, painlessly, on demand. In the end, physicians have to have a very good conceptual understanding of static equilibrium in order to help their patients acheive it and maintain it in the many aspects of the “mechanical” operation of the human body where it is essential.

For this reason, no matter who you are taking this course, you need to learn to solve real statics

125Wikipedia: http://www.wikipedia.org/wiki/House of cards. Yes, even this has a wikipedia entry. Pretty cool, actually!

problems, ones that can help you later understand and work with statics as your life and career demand. This may be nothing more than helping your kid build a stable tree house, but y’know, you don’t want to help them build a tree house and have that house fall out of the tree with your kid in it, nor do you want to deny them the joy of hanging out in their own tree house up in the trees!

As has been our habit from the beginning of the course, we start by considering the simplest problems in static equilibrium and then move on to more di cult ones. The simplest problems cannot, alas, be truly one dimensional because if the forces involved are truly one dimensional (and act to the right or left along a single line) there is no possible torque and force equilibrium su ces for both.

The simplest problem involving both force and torque is therefore at least three dimensional – two dimensional as far as the forces are concerned and one dimensional as far as torque and rotation is concerned. In other words, it will involve force balance in some plane of (possible) rotation and torque balance perpendicular to this plane alone a (possible) axis of rotation.

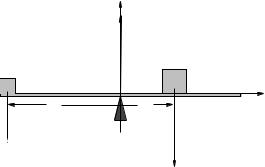
Example 7.2.1: Balancing a See-Saw

m1 g

m 2 g

Figure 93: You are given m1, x1, and x2 and are asked to find m2 and F such that the see-saw is in static equilibrium.

One typical problem in statics is balancing weights on a see-saw type arrangement – a uniform plank supported by a fulcrum in the middle. This particular problem is really only one dimensional as far as force is concerned, as there is no force acting in the x-direction or z-direction. It is one dimensional as far as torque is concerned, with rotation around any pivot one might select either into or out of the paper.

Static equilibrium requires force balance (one equation) and torque balance (one equation) and therefore we can solve for pretty much any two variables (unknowns) visible in figure 93 above. Let’s imagine that in this particular problem, the mass m1 and the distances x1 and x2 are given, and we need to find m2 and F .

We have two choices to make – where we select the pivot and which direction (in or out of the page) we are going to define to be “positive”. A perfectly reasonable (but not unique or necessarily “best”) choice is to select the pivot at the fulcrum of the see-saw where the unknown force F is exerted, and to select the +z-axis as positive rotation (out of the page as drawn).

We then write:

This is almost embarrassingly simple to solve. From the second equation:

It is worth noting that this is precisely the mass that moves the center of mass of the system so that it is square over the fulcrum/pivot.

From the first equation and the solution for m2:

That’s all there is to it! Obviously, we could have been given m1 and m2 and x1 and been asked to find x2 and F , etc, just as easily.

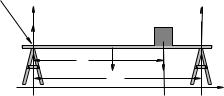
Example 7.2.2: Two Saw Horses

pivot

Figure 94: Two saw horses separated by a distance L support a plank of mass m symmetrically placed across them as shown. A block of mass M is placed on the plank a distance x from the saw horse on the left.

In figure 94, two saw horses separated by a distance L support a symmetrically placed plank. The rigid plank has mass m and supports a block of mass M placed a distance x from the left-hand saw horse. Find F1 and F2, the upward (normal) force exerted by each saw horse in order for this system to be in static equilibribum.

First let us pick something to put into equilibrium. The saw horses look pretty stable. The mass

Mdoes need to be in equilibrium, but that is pretty trivial – the plank exerts a normal force on

Mequal to its weight. The only tricky thing is the plank itself, which could and would rotate or collapse if F1 and F2 don’t correctly balance the load created by the weight of the plank plus the weight of the mass M .

Again there are no forces in x or z, so we simply ignore those directions. In the y direction:

or “the two saw horses must support the total weight of the plank plus the block”, F1 + F2 = (m + M )g. This is not unreasonable or even unexpected, but it doesn’t tell us how this weight is distributed between the two saw horses.

Once again we much choose a pivot. Four possible points – the point on the left-hand saw horse where F1 is applied, the point at L/2 that is the center of mass of the plank (and half-way in between the two saw horses), the point under mass M where its gravitational force acts, and the point on the right-hand saw horse where F2 is applied. Any of these will eliminate the torque due to one of the forces and presumably will simplify the problem relative to more arbitrary points. We select the left-hand point as shown – why not?

Then:

states that the torque around this pivot must be zero. We can easily solve for F2:

Does this make sense? Sure. The two saw horses share the weight of the symmetrically placed plank, obviously. The saw horse closest to the block M supports most of its weight, in a completely symmetric way. In the picture above, with x > L/2, that is saw horse 2, but if x < L/2, it would have been saw horse 1. In the middle, where x = L/2, the two saw horses symmetrically share the weight of the block as well!

This picture and solution are worth studying until all of this makes sense. Carrying things like sofas and tables (with the load shared between a person on either end) is a frequent experience, and from the solution to this problem you can see that if the load is not symmetrical, the person closest to the center of gravity will carry the largest load.

Let’s do a slightly more di cult one, one involving equilibrium in two force directions (and one torque direction). This will allow us to solve for three unknown quantities.

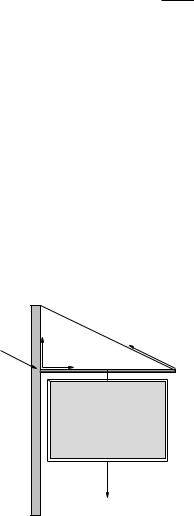
Example 7.2.3: Hanging a Tavern Sign

Figure 95: A sign with mass m is hung from a massless rigid pole of length L attached to a post and suspended by means of a wire at an angle θ relative to the horizontal.

Suppose that one day you get tired being a hardworking professional and decide to give it all up and open your own tavern/brewpub. Naturally, you site it in a lovely brick building close to campus (perhaps in Brightleaf Square). To attract passers-by you need a really good sign – the old fashioned sort made out of solid oak that hangs from a pole, one that (with the pole) masses m = 50 kg.

However, you really don’t want the sign to either punch through the brick wall or break the suspension wire you are going to use to support the end farthest from the wall and you don’t trust your architect because he seems way too interested in your future wares, so you decide to work out for yourself just what the forces are that the wall and wire have to support, as a function of the angle θ between the support pole and the support wire.

The physical arrangement you expect to end up with is shown in figure 95. You wish to find Fx, Fy and T , given m and θ.