magnitude of the outgoing momenta, and if we know the outgoing direction alone of either particle we can find everything – the magnitude and direction of the other particle’s momentum and the magnitude of the momentum of the particle whose angle we measured.

As you can see, this is all pretty di cult, so we’ll leave it at this point as a partially solved problem, ready to be tackled again for specific interactions or collision models in a future course.

4.8: Inelastic Collisions

A fully inelastic collision is where two particles collide and stick together. As always, momentum is conserved in the impact approximation, but now kinetic energy is not! In fact, we will see that macroscopic kinetic energy is always lost in an inelastic collision, either to heat or to some sort of mechanism that traps and reversibly stores the energy.

These collisions are much easier to understand and analyze than elastic collisions. That is because there are fewer degrees of freedom in an inelastic collision – we can easily solve them even in 2 or 3 dimensions. The whole solution is developed from

In other words, in a fully inelastic collision, the velocity of the outgoing combined particle is the velocity of the center of mass of the system, which we can easily compute from a knowledge of the initial momenta or velocities and masses. Of course! How obvious! How easy!

From this relation you can easily find ~vf in any number of dimensions, and answer many related questions. The collision is “solved”. However, there are a number of di erent kinds of problems one can solve given this basic solution – things that more or less tag additional physics problems on to the end of this initial one and use its result as their starting point, so you have to solve two or more subproblems in one long problem, one of which is the “inelastic collision”. This is best illustrated in some archetypical examples.

Example 4.8.1: One-dimensional Fully Inelastic Collision (only)

m1 m2 vf

Figure 56: Two blocks of mass m1 and m2 collide and stick together on a frictionless table.

In figure 56 above, a block m1 is sliding across a frictionless table at speed v0 to strike a second block m2 initially at rest, whereupon they stick together and move together as one thereafter at some final speed vf .

Before, after, and during the collision, gravity acts but is opposed by a normal force. There is no friction or drag force doing any work. The only forces in play are the internal forces mediating the collision and making the blocks stick together. We therefore know that momentum is conserved in this problem independent of the features of that internal interaction. Even if friction or drag forces did act, as long as the collision took place “instantly” in the impact approximation, momentum would

216 Week 4: Systems of Particles, Momentum and Collisions

still be conserved from immediately before to immediately after the collision, when the impulse p of the collision force would be much, much larger than any change in momentum due to the drag over the same small time t.

A traditional question that accompanies this is: How much kinetic energy was lost in the collision? We can answer this by simply figuring it out.

where we have expressed the result as a fraction of the initial kinetic energy!

Xcm

After Collision

m1 + m2

Xcm

Figure 57: Two blocks collide and stick together on a frictionless table – in the center of mass frame. After the collision they are both at rest at the center of mass and all of the kinetic energy they had before the collision in this frame is lost.

There is a di erent way to think about the collision and energy loss. In figure 57 you see the same collision portrayed in the CM frame. In this frame, the two particles always come together and stick to remain, at rest, at the center of mass after the collision. All of the kinetic energy in

the CM frame is lost in the collision! That’s exactly the amount we just computed, but I’m leaving the proof of that as an exercise for you.

Note well the BB limits: For a light bb (m1) striking a massive BB (m2), nearly all the energy is lost. This sort of collision between an asteroid (bb) and the earth (BB) caused at least one of the mass extinction events, the one that ended the Cretaceous and gave mammals the leg up that they needed in a world dominated (to that point) by dinosaurs. For a massive BB (m1) stricking a light bb (m2) very little of the energy of the massive object is lost. Your truck hardly slows when it smushes a bug “inelastically” against the windshield. In the equal billiard ball bb collision (m1 = m2), exactly one half of the initial kinetic energy is lost.

A similar collision in 2D is given for your homework, where a truck and a car inelastically collide and then slide down the road together. In this problem friction works, but not during the collision! Only after the “instant” (impact approximation) collision do we start to worry about the e ect of friction.

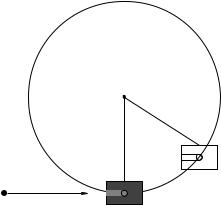
Example 4.8.2: Ballistic Pendulum

Figure 58: The “ballistic pendulum”, where a bullet strikes and sticks to/in a block, which then swings up to a maximum angle θf before stopping and swinging back down.

The classic ballistic pendulum question gives you the mass of the block M , the mass of the bullet m, the length of a string or rod suspending the “target” block from a free pivot, and the initial velocity of the bullet v0. It then asks for the maximum angle θf through which the pendulum swings after the bullet hits and sticks to the block (or alternatively, the maximum height H through which it swings). Variants abound – on your homework you might be asked to find the minimum speed v0 the bullet must have in order the the block whirl around in a circle on a never-slack string, or on the end of a rod. Still other variants permit the bullet to pass through the block and emerge with a di erent (smaller) velocity. You should be able to do them all, if you completely understand this example (and the other physics we have learned up to now, of course).

There is an actual lab that is commonly done to illustrate the physics; in this lab one typically measures the maximum horizontal displacement of the block, but it amounts to the same thing once one does the trigonometry.

The solution is simple:

•During the collision momentum is conserved in the impact approximation, which in this case basically implies that the block has no time to swing up appreciably “during” the actual collision.

•After the collision mechanical energy is conserved. Mechanical energy is not conserved during the collision (see solution above of straight up inelastic collision).

One can replace the second sub-problem with any other problem that requires a knowledge of either vf or Kf immediately after the collision as its initial condition. Ballistic loop-the-loop problems are entirely possible, in other words!

At this point the algebra is almost anticlimactic: The collision is one-dimensional (in the x- direction). Thus (for block M and bullet m) we have momentum conservation:

Now if we were foolish we’d evaluate vM +m,f to use in the next step: mechanical energy conservation. Being smart, we instead do the kinetic part of mechanical energy conservation in terms of momentum:

which only has a solution if mv0 is less than some maximum value. What does it mean if it is greater than this value (there is no inverse cosine of an argument with magnitude bigger than 1)? Will this answer “work” if θ > π/2, for a string? For a rod? For a track?

Don’t leave your common sense at the door when solving problems using algebra!

Example 4.8.3: Partially Inelastic Collision

Let’s briefly consider the previous example in the case where the bullet passes through the block and emerges on the far side with speed v1 < v0 (both given). How is the problem going to be di erent?

Not at all, not really. Momentum is still conserved during the collision, mechanical energy after. The only two di erences are that we have to evaluate the speed vf of the block M after the collision from this equation:

We can read this as “the momentum transferred to the block is the momentum lost by the bullet” because momentum is conserved. Given vf of the block only, you should be able to find e.g. the kinetic energy lost in this collision or θf or whatever in any of the many variants involving slightly di erent “after”-collision subproblems.