Homework for Week 9

Problem 1.

Physics Concepts: Make this week’s physics concepts summary as you work all of the problems in this week’s assignment. Be sure to cross-reference each concept in the summary to the problem(s) they were key to, and include concepts from previous weeks as necessary. Do the work carefully enough that you can (after it has been handed in and graded) punch it and add it to a three ring binder for review and study come finals!

Problem 2.

Harmonic oscillation is conceptually very important because (as has been remarked in class) many things that are stable will oscillate more or less harmonically if perturbed a small distance away from their stable equilibrium point. Draw an energy diagram, a graph of a “generic” interaction potential energy with a stable equilibrium point and explain in words and equations where, and why, this should be.

Problem 3.

A pendulum with a string of length L supporting a mass m on the earth has a certain period T . A physicist on the moon, where the acceleration near the surface is around g/6, wants to make a pendulum with the same period. What mass mm and length Lm of string could be used to accomplish this?

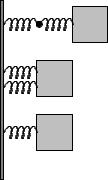
Problem 4.

m

k 1

m

k 2

m

k eff

In the figure above identical masses m are attached to two springs k1 and k2 in “series” – one connected to the other end-to-end – and in “parallel” – the two springs side by side. In the third picture another identical mass m is shown attached to a single spring with constant ke .

Note that this problem illustrates the scaling of Young’s modulus with length (series) or area (parallel). It also gives you a head start on how series and parallel addition of resistors and capacitors works next semester! It’s therefore well worth puzzling over.

Problem 5.

In this class we usually idealize fluid flow by neglecting resistance (drag) and the viscosity of the fluid as it passes through cylindrical pipes so we can use the Bernoulli equation. As discussed in class, however, it is often necessary to have at sound conceptual understanding of at least the qualitative e ects of including the resistance and viscosity. Use Poiseuille’s Law and the concepts of resistance, pressure, and flow from the online textbook to answer and discuss the following simple questions. Make sure your conceptual understanding of these concepts is qualitatively sound!

a)Is Pa = Pleft −Pright greater than, less than, or equal to zero in figure a) above, where blood flows at a rate Iv horizontally through a blood vessel with constant radius r and some length L against the resistance of that vessel?

b)If the radius r increases (while flow Iv and length L remain the same as in a), does the

Blood viscosity is chemically related to things like the “stickiness” of platelets and their abundance in the blood. Viscosity and the radius r of blood vessels can be regulated or altered (within limits) by drugs, disease, diet and exercise – all of which have a completely understandable e ect upon blood pressure based on the simple ideas above.

Problem 6.

A

2H/3 H

water

This problem will help you learn required concepts such as:

•Static equilibrium

•Archimedes Principle

•Simple Harmonic Oscillation

so please review them before you begin.

rgb is fishing in still water o of the old dock. He is using a cylindrical bobber as shown. The bobber has a cross sectional area of A and a length of H, and is balanced so that it remains vertical in the water. When it is floating at equilibrium (supporting the weight of the hook and worm dangling underneath) 2H/3 of its length is submerged in the water. You can neglect the volume of the line, hook and worm (that is, their buoyancy is negligible), and neglect all drag/damping forces. Answer the following questions in terms of A, H, ρw (the density of water), g:

a)What is the combined mass M of the bobber, hook and worm from the data?

b)A fish gives a tug on the worm and pulls the bobber straight down an additional distance (from equilibrium) y. What is the net restoring force on the bobber as a function of y?

c)Use this force and the calculated mass M from a) to write Newton’s 2nd Law for the motion of the bobber up and down (in y) and turn it into an equation of motion in standard form for a harmonic oscillator.

d)Assume that the bobber is pulled down the specific distance y = H/3 and released from rest at time t = 0. Neglecting the damping e ects of the water, write an equation for the displacement of the bobber from its equilibrium depth as a function of time, y(t) (the solution to the equation of motion).

e)With what frequency does the bobber bob? Evaluate your answer for H = 10 cm, A = 1 cm2 (reasonable values for a fishing bobber).

Problem 7.

L θmax

M

This problem will help you learn required concepts such as:

•Simple Harmonic Oscillation

•Torque

•Newton’s Second Law for Rotation

•Moments of Inertia

•Small Angle Approximation

so please review them before you begin.

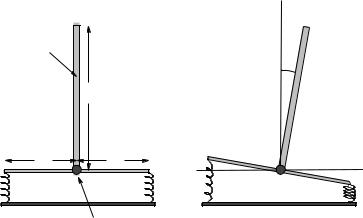
A grandfather clock is constructed with a pendulum that consists of a long, light (assume massless) rod and a small, heavy (assume point-like) mass M that can be slid up and down the rod changing L to “tune” the clock. The clock keeps perfect time when the period of oscillation of the pendulum is T = 2 seconds. When the clock is running, the maximum angle the rod makes with the vertical is θmax = 0.05 radians (a “small angle”).

a)Derive the equation of motion for the rod when it freely swings and solve for θ(t) assuming it starts at θmax at t = 0. You may use either force or torque.

b)At what distance L from the pivot should the mass be set so that the clock keeps correct time? As always, solve the problem algebraically first and only then worry about numbers.

c)In your answer above, you idealized by assuming the rod to be massless and the ball to be pointlike. In the real world, of course, the rod has a small mass m and the ball is a ball of radius r, not a point mass. Will the clock run slow or fast if you set the mass exactly where you computed it in part b)? Should you reduce L or increase L a bit to compensate and get better time? Explain.

Problem 8.

This problem will help you learn required concepts such as:

•Simple Harmonic Oscillation

•Springs (Hooke’s Law)

•Small Angle Approximation

so please review them before you begin.

The pole in the figure has mass M and length h is supported by two identical springs with spring constant k that connect its platform to a table as shown. The springs attach to the platform a distance d from the base of the pole, which is pivoted on a frictionless hinge so it can rotate only in the plane of the page as shown. Gravity acts down. Neglect the mass of the platform.

a)On a copy of the right-hand figure, indicate the forces acting on the pole and platform when the pole tips over as shown, deviating from the vertical by a (small) angle θ.

b)Using your answer to a), find the total torque acting on the system (pole and platform) about the hinged bottom of the pole, and note its direction. Use the small angle approximations sin(θ) ≈ θ; cos(θ) ≈ 1.

c)Find the minimal value for the spring constant k of the two springs such that the pole is stable in the vertical position. This means that a small deviation as above produces a torque that restores the pole to the vertical.

d)For M = 50 kg, h = 1.0 meter, d = 0.5 meter, and springs with spring constant k = 9600 N/m, find the angular frequency with which the pole oscillates about the vertical.

Advanced Problem 9.

P0 A

y P0

a

This problem will help you learn required concepts such as:

•Bernoulli’s Equation

•Torricelli’s Law

so please review them before you begin.

In the figure above, a large drum of water is open at the top and filled up to a height y above a tap at the bottom (which is also open to normal air pressure). The drum has a cross-sectional area A at the top and the tap has a cross sectional area of a at the bottom.

The questions below help you use calculus to determine how long it will take for the drum to empty. The first two questions and the last question anybody can answer. The one where you actually have to integrate may be di cult for non-math/physics/engineering students, but feel free to give it a try!

a)Find the speed with which the water emerges from the tap. Assume laminar flow without resistance. Compare your answer to the speed a mass has after falling a height y in a uniform gravitational field (after using A a to simplify your final answer, Torricelli’s Law).

b)Start by guessing how long it will take water to flow out of the tank by using dimensional analysis and the insight gained from a). That is, think about how you expect the time to vary with each quantity that describes the problem and form a simple expression with the relevant parameters that has the right units and goes up where it should go up and down where it should go down.

c)Next, find an algebraic expression for the velocity of the top. This is dy/dt.

d)Manupulate the expression and integrate dy on one side, an expression with dt on the other side, to find the time it takes for the top of the water to reach the bottom of the tank. Compare your answer to b) to your answer to d) and the time it takes a mass to fall a height y in a uniform gravitational field. Does the correct answer make dimensional and physical sense? You might want to think a bit about Toricelli’s Law here as well...

e)Evaluate the answers to a) and d) for A = 0.50 m2, a = 0.5 cm2, y(0) = 100 cm.

Optional Problems

Continue studying for the final exam! Only three “weeks” (chapters) to go in this textbook, finals are coming apace!