
- •Preface
- •Textbook Layout and Design
- •Preliminaries
- •See, Do, Teach
- •Other Conditions for Learning
- •Your Brain and Learning
- •The Method of Three Passes
- •Mathematics
- •Summary
- •Homework for Week 0
- •Summary
- •1.1: Introduction: A Bit of History and Philosophy
- •1.2: Dynamics
- •1.3: Coordinates
- •1.5: Forces
- •1.5.1: The Forces of Nature
- •1.5.2: Force Rules
- •Example 1.6.1: Spring and Mass in Static Force Equilibrium
- •1.7: Simple Motion in One Dimension
- •Example 1.7.1: A Mass Falling from Height H
- •Example 1.7.2: A Constant Force in One Dimension
- •1.7.1: Solving Problems with More Than One Object
- •Example 1.7.4: Braking for Bikes, or Just Breaking Bikes?
- •1.8: Motion in Two Dimensions
- •Example 1.8.1: Trajectory of a Cannonball
- •1.8.2: The Inclined Plane
- •Example 1.8.2: The Inclined Plane
- •1.9: Circular Motion
- •1.9.1: Tangential Velocity
- •1.9.2: Centripetal Acceleration
- •Example 1.9.1: Ball on a String
- •Example 1.9.2: Tether Ball/Conic Pendulum
- •1.9.3: Tangential Acceleration
- •Homework for Week 1
- •Summary
- •2.1: Friction
- •Example 2.1.1: Inclined Plane of Length L with Friction
- •Example 2.1.3: Find The Minimum No-Skid Braking Distance for a Car
- •Example 2.1.4: Car Rounding a Banked Curve with Friction
- •2.2: Drag Forces
- •2.2.1: Stokes, or Laminar Drag
- •2.2.2: Rayleigh, or Turbulent Drag
- •2.2.3: Terminal velocity
- •Example 2.2.1: Falling From a Plane and Surviving
- •2.2.4: Advanced: Solution to Equations of Motion for Turbulent Drag
- •Example 2.2.3: Dropping the Ram
- •2.3.1: Time
- •2.3.2: Space
- •2.4.1: Identifying Inertial Frames
- •Example 2.4.1: Weight in an Elevator
- •Example 2.4.2: Pendulum in a Boxcar
- •2.4.2: Advanced: General Relativity and Accelerating Frames
- •2.5: Just For Fun: Hurricanes
- •Homework for Week 2
- •Week 3: Work and Energy
- •Summary
- •3.1: Work and Kinetic Energy
- •3.1.1: Units of Work and Energy
- •3.1.2: Kinetic Energy
- •3.2: The Work-Kinetic Energy Theorem
- •3.2.1: Derivation I: Rectangle Approximation Summation
- •3.2.2: Derivation II: Calculus-y (Chain Rule) Derivation
- •Example 3.2.1: Pulling a Block
- •Example 3.2.2: Range of a Spring Gun
- •3.3: Conservative Forces: Potential Energy
- •3.3.1: Force from Potential Energy
- •3.3.2: Potential Energy Function for Near-Earth Gravity
- •3.3.3: Springs
- •3.4: Conservation of Mechanical Energy
- •3.4.1: Force, Potential Energy, and Total Mechanical Energy
- •Example 3.4.1: Falling Ball Reprise
- •Example 3.4.2: Block Sliding Down Frictionless Incline Reprise
- •Example 3.4.3: A Simple Pendulum
- •Example 3.4.4: Looping the Loop
- •3.5: Generalized Work-Mechanical Energy Theorem
- •Example 3.5.1: Block Sliding Down a Rough Incline
- •Example 3.5.2: A Spring and Rough Incline
- •3.5.1: Heat and Conservation of Energy
- •3.6: Power
- •Example 3.6.1: Rocket Power
- •3.7: Equilibrium
- •3.7.1: Energy Diagrams: Turning Points and Forbidden Regions
- •Homework for Week 3
- •Summary
- •4.1: Systems of Particles
- •Example 4.1.1: Center of Mass of a Few Discrete Particles
- •4.1.2: Coarse Graining: Continuous Mass Distributions
- •Example 4.1.2: Center of Mass of a Continuous Rod
- •Example 4.1.3: Center of mass of a circular wedge
- •4.2: Momentum
- •4.2.1: The Law of Conservation of Momentum
- •4.3: Impulse
- •Example 4.3.1: Average Force Driving a Golf Ball
- •Example 4.3.2: Force, Impulse and Momentum for Windshield and Bug
- •4.3.1: The Impulse Approximation
- •4.3.2: Impulse, Fluids, and Pressure
- •4.4: Center of Mass Reference Frame
- •4.5: Collisions
- •4.5.1: Momentum Conservation in the Impulse Approximation
- •4.5.2: Elastic Collisions
- •4.5.3: Fully Inelastic Collisions
- •4.5.4: Partially Inelastic Collisions
- •4.6: 1-D Elastic Collisions
- •4.6.1: The Relative Velocity Approach
- •4.6.2: 1D Elastic Collision in the Center of Mass Frame
- •4.7: Elastic Collisions in 2-3 Dimensions
- •4.8: Inelastic Collisions
- •Example 4.8.1: One-dimensional Fully Inelastic Collision (only)
- •Example 4.8.2: Ballistic Pendulum
- •Example 4.8.3: Partially Inelastic Collision
- •4.9: Kinetic Energy in the CM Frame
- •Homework for Week 4
- •Summary
- •5.1: Rotational Coordinates in One Dimension
- •5.2.1: The r-dependence of Torque
- •5.2.2: Summing the Moment of Inertia
- •5.3: The Moment of Inertia
- •Example 5.3.1: The Moment of Inertia of a Rod Pivoted at One End
- •5.3.1: Moment of Inertia of a General Rigid Body
- •Example 5.3.2: Moment of Inertia of a Ring
- •Example 5.3.3: Moment of Inertia of a Disk
- •5.3.2: Table of Useful Moments of Inertia
- •5.4: Torque as a Cross Product
- •Example 5.4.1: Rolling the Spool
- •5.5: Torque and the Center of Gravity
- •Example 5.5.1: The Angular Acceleration of a Hanging Rod
- •Example 5.6.1: A Disk Rolling Down an Incline
- •5.7: Rotational Work and Energy
- •5.7.1: Work Done on a Rigid Object
- •5.7.2: The Rolling Constraint and Work
- •Example 5.7.2: Unrolling Spool
- •Example 5.7.3: A Rolling Ball Loops-the-Loop
- •5.8: The Parallel Axis Theorem
- •Example 5.8.1: Moon Around Earth, Earth Around Sun
- •Example 5.8.2: Moment of Inertia of a Hoop Pivoted on One Side
- •5.9: Perpendicular Axis Theorem
- •Example 5.9.1: Moment of Inertia of Hoop for Planar Axis
- •Homework for Week 5
- •Summary
- •6.1: Vector Torque
- •6.2: Total Torque
- •6.2.1: The Law of Conservation of Angular Momentum
- •Example 6.3.1: Angular Momentum of a Point Mass Moving in a Circle
- •Example 6.3.2: Angular Momentum of a Rod Swinging in a Circle
- •Example 6.3.3: Angular Momentum of a Rotating Disk
- •Example 6.3.4: Angular Momentum of Rod Sweeping out Cone
- •6.4: Angular Momentum Conservation
- •Example 6.4.1: The Spinning Professor
- •6.4.1: Radial Forces and Angular Momentum Conservation
- •Example 6.4.2: Mass Orbits On a String
- •6.5: Collisions
- •Example 6.5.1: Fully Inelastic Collision of Ball of Putty with a Free Rod
- •Example 6.5.2: Fully Inelastic Collision of Ball of Putty with Pivoted Rod
- •6.5.1: More General Collisions
- •Example 6.6.1: Rotating Your Tires
- •6.7: Precession of a Top
- •Homework for Week 6
- •Week 7: Statics
- •Statics Summary
- •7.1: Conditions for Static Equilibrium
- •7.2: Static Equilibrium Problems
- •Example 7.2.1: Balancing a See-Saw
- •Example 7.2.2: Two Saw Horses
- •Example 7.2.3: Hanging a Tavern Sign
- •7.2.1: Equilibrium with a Vector Torque
- •Example 7.2.4: Building a Deck
- •7.3: Tipping
- •Example 7.3.1: Tipping Versus Slipping
- •Example 7.3.2: Tipping While Pushing
- •7.4: Force Couples
- •Example 7.4.1: Rolling the Cylinder Over a Step
- •Homework for Week 7
- •Week 8: Fluids
- •Fluids Summary
- •8.1: General Fluid Properties
- •8.1.1: Pressure
- •8.1.2: Density
- •8.1.3: Compressibility
- •8.1.5: Properties Summary
- •Static Fluids
- •8.1.8: Variation of Pressure in Incompressible Fluids
- •Example 8.1.1: Barometers
- •Example 8.1.2: Variation of Oceanic Pressure with Depth
- •8.1.9: Variation of Pressure in Compressible Fluids
- •Example 8.1.3: Variation of Atmospheric Pressure with Height
- •Example 8.2.1: A Hydraulic Lift
- •8.3: Fluid Displacement and Buoyancy
- •Example 8.3.1: Testing the Crown I
- •Example 8.3.2: Testing the Crown II
- •8.4: Fluid Flow
- •8.4.1: Conservation of Flow
- •Example 8.4.1: Emptying the Iced Tea
- •8.4.3: Fluid Viscosity and Resistance
- •8.4.4: A Brief Note on Turbulence
- •8.5: The Human Circulatory System
- •Example 8.5.1: Atherosclerotic Plaque Partially Occludes a Blood Vessel
- •Example 8.5.2: Aneurisms
- •Homework for Week 8
- •Week 9: Oscillations
- •Oscillation Summary
- •9.1: The Simple Harmonic Oscillator
- •9.1.1: The Archetypical Simple Harmonic Oscillator: A Mass on a Spring
- •9.1.2: The Simple Harmonic Oscillator Solution
- •9.1.3: Plotting the Solution: Relations Involving
- •9.1.4: The Energy of a Mass on a Spring
- •9.2: The Pendulum
- •9.2.1: The Physical Pendulum
- •9.3: Damped Oscillation
- •9.3.1: Properties of the Damped Oscillator
- •Example 9.3.1: Car Shock Absorbers
- •9.4: Damped, Driven Oscillation: Resonance
- •9.4.1: Harmonic Driving Forces
- •9.4.2: Solution to Damped, Driven, Simple Harmonic Oscillator
- •9.5: Elastic Properties of Materials
- •9.5.1: Simple Models for Molecular Bonds
- •9.5.2: The Force Constant
- •9.5.3: A Microscopic Picture of a Solid
- •9.5.4: Shear Forces and the Shear Modulus
- •9.5.5: Deformation and Fracture
- •9.6: Human Bone
- •Example 9.6.1: Scaling of Bones with Animal Size
- •Homework for Week 9
- •Week 10: The Wave Equation
- •Wave Summary
- •10.1: Waves
- •10.2: Waves on a String
- •10.3: Solutions to the Wave Equation
- •10.3.1: An Important Property of Waves: Superposition
- •10.3.2: Arbitrary Waveforms Propagating to the Left or Right
- •10.3.3: Harmonic Waveforms Propagating to the Left or Right
- •10.3.4: Stationary Waves
- •10.5: Energy
- •Homework for Week 10
- •Week 11: Sound
- •Sound Summary
- •11.1: Sound Waves in a Fluid
- •11.2: Sound Wave Solutions
- •11.3: Sound Wave Intensity
- •11.3.1: Sound Displacement and Intensity In Terms of Pressure
- •11.3.2: Sound Pressure and Decibels
- •11.4: Doppler Shift
- •11.4.1: Moving Source
- •11.4.2: Moving Receiver
- •11.4.3: Moving Source and Moving Receiver
- •11.5: Standing Waves in Pipes
- •11.5.1: Pipe Closed at Both Ends
- •11.5.2: Pipe Closed at One End
- •11.5.3: Pipe Open at Both Ends
- •11.6: Beats
- •11.7: Interference and Sound Waves
- •Homework for Week 11
- •Week 12: Gravity
- •Gravity Summary
- •12.1: Cosmological Models
- •12.2.1: Ellipses and Conic Sections
- •12.4: The Gravitational Field
- •12.4.1: Spheres, Shells, General Mass Distributions
- •12.5: Gravitational Potential Energy
- •12.6: Energy Diagrams and Orbits
- •12.7: Escape Velocity, Escape Energy
- •Example 12.7.1: How to Cause an Extinction Event
- •Homework for Week 12

Week 5: Torque and Rotation in One Dimension |
265 |
Homework for Week 5
Problem 1.
Physics Concepts: Make this week’s physics concepts summary as you work all of the problems in this week’s assignment. Be sure to cross-reference each concept in the summary to the problem(s) they were key to, and include concepts from previous weeks as necessary. Do the work carefully enough that you can (after it has been handed in and graded) punch it and add it to a three ring binder for review and study come finals!
Problem 2.
This problem will help you learn required concepts such as:
•Definition/Evaluation of Moment of Inertia
•Parallel Axis Theorem
so please review them before you begin.
a)Evaluate the moment of inertia of a uniform rod of mass M and length L about its center of mass by direct integration.
pivot
|
y |
|
−L/2 |
L/2 |
x |
|
b)Evaluate the moment of inertia of a uniform rod of mass M and length L about one end by direct integration. Also evaluate it using the parallel axis theorem and the result you just obtained. Which is easier?
pivot
y |
|
L |
x |
|
266 Week 5: Torque and Rotation in One Dimension
Problem 3.
This problem will help you learn required concepts such as:
•Definition/Evaluation of Moment of Inertia
•Parallel Axis Theorem
so please review them before you begin.
a)Evaluate the moment of inertia of a uniform disk of mass M and radius R about its axis of symmetry by direct integration (this can be set up as a “one dimensional integral” and hence is not too di cult).
pivot
c) 
b)Evaluate the moment of inertia of this disk around a pivot at the edge of the disk (for example, a thin nail stuck through a hole at the outer edge) using the parallel axis theorem. Would you care to do the actual integral to find the moment of inertia of the disk in this case?
pivot
d)

Week 5: Torque and Rotation in One Dimension |
267 |
Problem 4.
M,R
H
 θ
θ
This problem will help you learn required concepts such as:
•Newton’s Second Law for Translation and Rotation
•Moment of Inertia
•Conservation of Mechanical Energy
•Static Friction
so please review them before you begin.
A round object with mass m and radius R is released from rest to roll without slipping down an inclined plane of height H at angle θ relative to horizontal. The object has a moment of inertia I = βmR2 (where β is a dimensionless number such as 12 or 25 , that might describe a disk or a solid ball, respectively).
a)Begin by relating v (the speed of the center of mass) to the angular velocity (for the rolling object). You will use this (and the related two equations for s and θ and a and α) repeatedly in rolling problems.
b)Using Newton’s second law in both its linear and rotational form plus the rolling constraint, show that the acceleration of the object is:
a= g sin(θ)
1+ β
c)Using conservation of mechanical energy, show that it arrives at the bottom of the incline with a velocity:
s
v =
2gH
1 + β
d) Show that the condition for the greatest angle for which the object will roll without slipping is
that:
1 tan(θ) ≤ (1 + β )µs
where µs is the coe cient of static friction between the object and the incline.
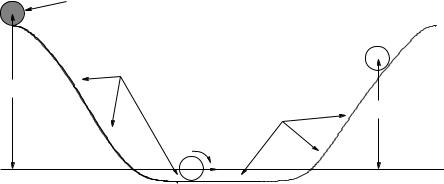
268 |
Week 5: Torque and Rotation in One Dimension |
Problem 5.
m,R
rough
H
icy H’
This problem will help you learn required concepts such as:
•Conservation of Mechanical Energy
•Rotational Kinetic Energy
•Rolling Constraint.
so please review them before you begin.
A disk of mass m and radius R rolls without slipping down a rough slope of height H onto an icy (frictionless) track at the bottom that leads up a second icy (frictionless) hill as shown.
a)How fast is the disk moving at the bottom of the first incline? How fast is it rotating (what is its angular velocity)?
b)Does the disk’s angular velocity change as it leaves the rough track and moves onto the ice (in the middle of the flat stretch in between the hills)?
c)How far up the second hill (vertically, find H′) does the disk go before it stops rising?

Week 5: Torque and Rotation in One Dimension |
269 |
Problem 6.
I (about cm) |
R |
mass m |
|
||
|
r |
F |
|
|
F
F
This problem will help you learn required concepts such as:
•Direction of torque
•Rolling Constraint
so please review them before you begin.
In the figure above, a spool of mass m is wrapped with string around the inner spool. The spool is placed on a rough surface (with coe cient of friction µs = 0.5) and the string is pulled with force
F0.5 mg in the three directions shown.
a)For each picture, indicate the direction that static friction will point. Can the spool slip while it rolls for this magnitude of force?
b)For each picture, indicate the direction that the spool will accelerate.
c)For each picture, find the magnitude of the force exerted by static friction and the magnitude of the acceleration of the spool in terms of r, R or Icm = βmR2.
Note: You can use either the center of mass or the point of contact with the ground (with the parallel axis theorem) as a pivot, the latter being slightly easier both algebraically and intuitively.

270 |
Week 5: Torque and Rotation in One Dimension |
Problem 7. |
|
R
M
m1 m2
H
This problem will help you learn required concepts such as:
•Newton’s Second Law
•Newton’s Second Law for Rotating Systems (torque and angular acceleration)
•Moments of Inertia
•The Rolling Constraint
•Conservation of Mechanical Energy
so please review them before you begin.
In the figure above Atwood’s machine is drawn – two masses m1 and m2 hanging over a massive pulley which you can model as a disk of mass M and radius R, connected by a massless unstretchable string. The string rolls on the pulley without slipping.
a)Draw three free body diagrams (isolated diagrams for each object showing just the forces acting on that object) for the three masses in the figure above.
b)Convert each free body diagram into a statement of Newton’s Second Law (linear or rotational) for that object.
c)Using the rolling constraint (that the pulley rolls without slipping as the masses move up or down) find the acceleration of the system and the tensions in the string on both sides of the pulley in terms of m1, m2, M , g, and R.
d)Suppose mass m2 > m1 and the system is released from rest with the masses at equal heights. When mass m2 has descended a distance H, use conservation of mechanical energy to find velocity of each mass and the angular velocity of the pulley.
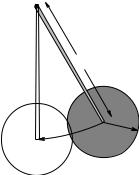
Week 5: Torque and Rotation in One Dimension |
271 |
Problem 8.
pivot
θ
R
r
M
This problem will help you learn required concepts such as:
•Newton’s Second Law for rotating objects
•Moment of Inertia
•Parallel Axis Theorem
•Work in rotating systems
•Rotational Kinetic Energy
•Kinetic Energy in Lab versus CM
so please review them before you begin.
In the picture above, a physical pendulum is constructed by hanging a disk of mass M and radius r on the end of a massless rigid rod in such a way that the center of mass of the disk is a distance R away from the pivot and so that the whole disk pivots with the rod. The pendulum is pulled to an initial angle θ0 (relative to vertically down) and then released.
a)Find the torque about the pivot exerted on the pendulum by gravity at an arbitrary angle θ.
b)Integrate the torque from θ = θ0 to θ = 0 to find the total work done by the gravitational torque as the pendulum disk falls to its lowest point. Note that your answer should be M gR(1− cos(θ0)) = M gH where H is the initial height above this lowest point.
c)Find the moment of inertia of the pendulum about the pivot (using the parallel axis theorem).
d) Set the work you evaluated in b) equal to the rotational kinetic energy of the disk |
1 Iω2 |
using |
||
|
dθ |
|
2 |
|
the moment of inertia you found in c). Solve for ω = |
when the disk is at its lowest point. |
|||
|
dt |
|
|
|
e) Show that this kinetic energy is equal to the kinetic energy of the moving center of mass of the disk 12 M v2 plus the kinetic energy of the disk’s rotation about its own center of mass, 12 Icmω2, at the lowest point.
As an optional additional step, write Newton’s Second Law in rotational coordinates τ = Iα (using the values for the magnitude of the torque and moment of inertia you determined above) and solve for the angular acceleration as a function of the angle θ. In a few weeks we will learn to solve this equation of motion for small angle oscillations, so it is good to practice obtaining it from the basic physics now.

272 |
Week 5: Torque and Rotation in One Dimension |
Problem 9.
m,r
H
R
This problem will help you learn required concepts such as:
•Newton’s Second Law
•Moments of Inertia
•Rotational Kinetic Energy
•The Rolling Constraint
•Conservation of Mechanical Energy
•Centripetal Acceleration
•Static Friction
so please review them before you begin.
A solid ball of mass M and radius r sits at rest at the top of a hill of height H leading to a circular loop-the-loop. The center of mass of the ball will move in a circle of radius R if it goes around the loop. Recall that the moment of inertia of a solid ball is Iball = 25 M R2.
a)Find the minimum height Hmin for which the ball barely goes around the loop staying on the track at the top, assuming that it rolls without slipping the entire time independent of the normal force.
b)How does your answer relate to the minimum height for the earlier homework problem where it was a block that slid around a frictionless track? Does this answer make sense? If it is higher, where did the extra potential energy go? If it is lower, where did the extra kinetic energy come from?
c)Discussion question for recitation: The assumption that the ball will roll around the track without slipping if released from this estimated minimum height is not a good one. Why not?
Week 5: Torque and Rotation in One Dimension |
273 |
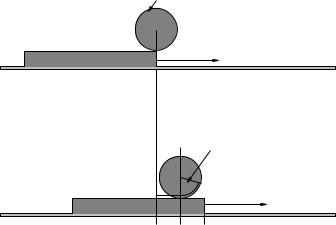
Advanced Problem 10.
m,R
F
M
θ
F
M
This problem will help you learn required concepts such as:
•Newton’s Second Law (linear and rotational)
•Rolling Constraint
•Static and Kinetic Friction
•Changing Coordinate Frames
so please review them before you begin.
A disk of mass m is resting on a slab of mass M , which in turn is resting on a frictionless table. The coe cients of static and kinetic friction between the disk and the slab are µs and µk,
~
respectively. A small force F to the right is applied to the slab as shown, then gradually increased.
~
a) When F is small, the slab will accelerate to the right and the disk will roll on the slab without slipping. Find the acceleration of the slab, the acceleration of the disk, and the angular acceleration of the disk as this happens, in terms of m, M , R, and the magnitude of the force
F .
b) Find the maximum force Fmax such that it rolls without slipping.
c) If F is greater than this, solve once again for the acceleration and angular acceleration of the disk and the acceleration of the slab.
Hint: The hardest single thing about this problem isn’t the physics (which is really pretty straightfoward). It is visualizing the coordinates as the center of mass of the disk moves with a di erent acceleration as the slab. I have drawn two figures above to help you with this – the lower figure represents a possible position of the disk after the slab has moved some distance to the right and the disk has rolled back (relative to the slab! It has moved forward relative to the ground! Why?) without slipping. Note the dashed radius to help you see the angle through which it has rolled and the various dashed lines to help you relate the distance the slab has moved xs, the distance the center of the disk has moved xd, and the angle through which it has rolled θ. Use this relation to connect the acceleration of the slab to the acceleration and angular acceleration of the disk.
If you can do this one, good job!

274 |
Week 5: Torque and Rotation in One Dimension |
Optional Problems
The following problems are not required or to be handed in, but are provided to give you some extra things to work on or test yourself with after mastering the required problems and concepts above and to prepare for quizzes and exams.
Optional Problem 11.
F
R
r
A cable spool of mass M , radius R and moment of inertia I = βM R2 is wrapped around its OUTER disk with fishing line and set on a rough rope as shown. The inner spool has a radius r. The fishing line is then pulled with a force F to the right so that it rolls down the rope without slipping.
a)Find the magnitude and direction of the acceleration of the spool.
b)Find the force (magnitude and direction) exerted by the friction of the rope on the spool.
c)For one particular value of r, the frictional force is zero!. Find that value. For larger values, which way does friction point? For smaller values, which way does friction point? At this value, if the rope were not there would the motion be any di erent?
In analyzing the “walking the spool” problem in class and in the text above, students often ask how they can predict which direction that static friction acts on a rolling spool, and I reply that they can’t! I can’t, not always, because in this problem it can point either way and which way it ultimately points depends on the details of R, r and β! The best you can do is make a reasonable guess as to the direction and let the algebra speak – if your answer comes out negative, friction points the other way.

Week 5: Torque and Rotation in One Dimension |
275 |
Optional Problem 12.
|
M |
M |
R M |
|
R |
M
This problem will help you learn required concepts such as:
•Moment of Inertia
•Newton’s Second Law (translational and rotational)
•Conservation of Mechanical Energy
so please review them before you begin.
A block of mass M sits on a smooth (frictionless) table. A mass M is suspended from an Acme (massless, unstretchable, unbreakable) rope that is looped around the two pulleys, each with the same mass M and radius R as shown and attached to the support of the rightmost pulley. The two pulleys each have the moment of inertia of a disk, I = 12 M R2 and the rope rolls on the pulleys without slipping. At time t = 0 the system is released at rest.
a)Draw free body diagrams for each of the four masses. Don’t forget the forces exerted by the bar that attaches the pulley to the mass on the left or the pulley on the right to the table! Note that some of these forces will cancel due to the constraint that the center of mass of certain masses moves only in one direction or does not move at all. Note also that the torque exerted by the weight of the pulley around the near corder of the mass on the table is not not enough to tip it over.
b)Write the relevant form(s) of Newton’s Second Law for each mass, translational and rotational as needed, separately, wherever the forces in some direction do not cancel. Also write the constraint equations that relate the accelerations (linear and angular) of the masses and pulleys.
c)Find the acceleration of the hanging mass M (only) in terms of the givens. Note that you can’t quite just add all of the equations you get after turning the torque equations into force equations, but if you solve the equations simultaneously, systematically eliminating all internal forces and tensions, you’ll get a simple enough answer.
d)Find the speed of the hanging mass M after it has fallen a height H, using conservation of total
mechanical energy. Show that it is consistent with the “usual” constant-acceleration-from-rest
√
answer v = 2aH for the acceleration found in c).
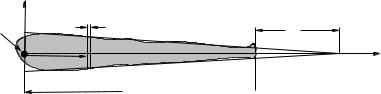
276 |
Week 6: Vector Torque and Angular Momentum |
Optional Problem 13.
dx
pivot |
x 0 |
x
L 
This problem will help you learn required concepts such as:
•Finding the Center of Mass using Integration
•Finding the Moment of Inertia using Integration
so please review them before you begin.
A simple model for the one-dimensional mass distribution of a human leg of length L and mass M is:
λ(x) = C · (L + x0 − x)
Note that this quantity is maximum at x = 0, varies linearly with x, and vanishes smoothly at x = L + x0. That means that it doesn’t reach λ = 0 when x = L, just as the mass per unit length of your leg doesn’t reach zero at your ankles.
a) Find the constant C in terms of M , L, and x0 by evaluating:
Z L
M = λ(x) dx
0
and solving for C.
b)Find the center of mass of the leg (as a distance down the leg from the hip/pivot at the origin). You may leave your answer in terms of C (now that you know it) or you can express it in terms of L and x0 only as you prefer.
c)Find the moment of inertia of the leg about the hip/pivot at the origin. Again, you may leave it in terms of C if you wish or express it in terms of M , L and x0. Do your answers all have the right units?
d)How might one improve the estimate of the moment of inertia to take into account the foot (as a lump of “extra mass” mf out there at x = L that doesn’t quite fit our linear model)?
This is, as you can see, something that an orthopedic specialist might well need to actually do with a much better model in order to e.g. outfit a patient with an artificial hip. True, they might use a computer to do the actual computations required, but is it plausible that they could possibly do what they need to do without knowing the physics involved in some detail?
