Homework for Week 3

Problem 1.

Physics Concepts: Make this week’s physics concepts summary as you work all of the problems in this week’s assignment. Be sure to cross-reference each concept in the summary to the problem(s) they were key to, and include concepts from previous weeks as necessary. Do the work carefully enough that you can (after it has been handed in and graded) punch it and add it to a three ring binder for review and study come finals!

Problem 2.

Derive the Work-Kinetic Energy (WKE) theorem in one dimension from Newton’s second law. You may use any approach used in class or given and discussed in this textbook (or any other), but do it yourself and without looking after studying.

Problem 3.

m

L

θ

D?

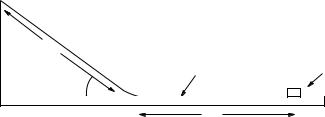
A block of mass m slides down a smooth (frictionless) incline of length L that makes an angle θ with the horizontal as shown. It then reaches a rough surface with a coe cient of kinetic friction

µk.

Use the concepts of work and/or mechanical energy to find the distance D the block slides across the rough surface before it comes to rest. You will find that using the generalized non-conservative work-mechanical energy theorem is easiest, but you can succeed using work and mechanical energy conservation for two separate parts of the problem as well.

Problem 4.

d

H

m

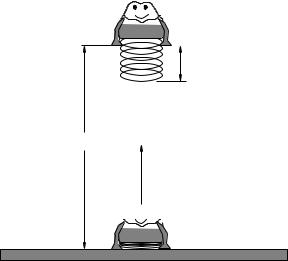
A simple child’s toy is a jumping frog made up of an approximately massless spring of uncompressed length d and spring constant k that propels a molded plastic “frog” of mass m. The frog is pressed down onto a table (compressing the spring by d) and at t = 0 the spring is released so that the frog leaps high into the air.

Use work and/or mechanical energy to determine how high the frog leaps.

Problem 5.

m2

m1

H

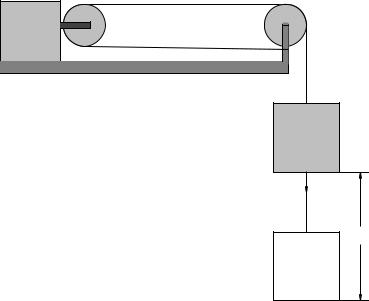
A block of mass m2 sits on a rough table. The coe cients of friction between the block and the table are µs and µk for static and kinetic friction respectively. A much larger mass m1 (easily heavy enough to overcome static friction) is suspended from a massless, unstretchable, unbreakable rope that is looped around the two pulleys as shown and attached to the support of the rightmost pulley. At time t = 0 the system is released at rest.

Use work and/or mechanical energy (where the latter is very easy since the internal work done by the tension in the string cancels) to find the speed of both masses after the large mass m1 has fallen a distance H. Note that you will still need to use the constraint between the coordinates that describe the two masses. Remember how hard you had to “work” to get this answer last week? When time isn’t important, energy is better!

Problem 6.

D

m

F = F oe−x/D

x

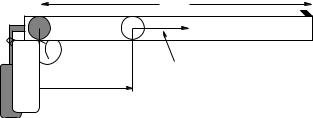
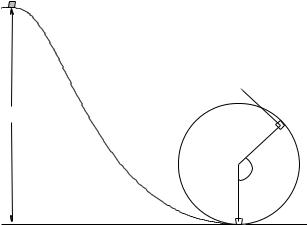
A simple schematic for a paintball gun with a barrel of length D is shown above; when the trigger is pulled carbon dioxide gas under pressure is released into the approximately frictionless barrel behind the paintball (which has mass m). As it enters, the expanding gas is cut o by a special valve so that it exerts a force on the ball of magnitude:

F = F0e−x/D

on the ball, pushing it to the right, where x is measured from the paintball’s initial position as shown, until the ball leaves the barrel.

a)Find the work done on the paintball by the force as the paintball is accelerated a total distance D down the barrel.

b)Use the work-kinetic-energy theorem to compute the kinetic energy of the paintball after it has been accelerated.

c)Find the speed with which the paintball emerges from the barrel after the trigger is pulled.

Problem 7.

m

v

H

R

θ

R

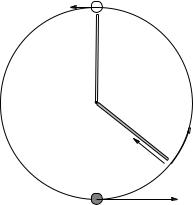
A block of mass M sits at rest at the top of a frictionless hill of height H leading to a circular frictionless loop-the-loop of radius R.

a)Find the minimum height Hmin for which the block barely goes around the loop staying on the track at the top. (Hint: What is the condition on the normal force when it “barely” stays in contact with the track? This condition can be thought of as “free fall” and will help us understand circular orbits later, so don’t forget it.).

Discuss within your recitation group why your answer is a scalar number times R and how this kind of result is usually a good sign that your answer is probably right.

b)If the block is started at height Hmin, what is the normal force exerted by the track at the bottom of the loop where it is greatest?

If you have ever ridden roller coasters with loops, use the fact that your apparent weight is the normal force exerted on you by your seat if you are looping the loop in a roller coaster and discuss with your recitation group whether or not the results you derive here are in accord with your experiences. If you haven’t, consider riding one aware of the forces that are acting on you and how they a ect your perception of weight and change your direction on your next visit to e.g. Busch Gardens to be, in a bizarre kind of way, a physics assignment. (Now c’mon, how many classes have you ever taken that assign riding roller coasters, even as an optional activity?:-)

Problem 8.

vmin

R

T m

vo

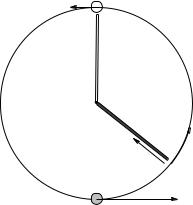
A ball of mass m is attached to a (massless, unstretchable) string and is suspended from a pivot. It is moving in a vertical circle of radius R such that it has speed v0 at the bottom as shown. The ball is in a vacuum; neglect drag forces and friction in this problem. Near-Earth gravity acts down.

a)Find an expression for the force exerted on the ball by the rod at the top of the loop as a function of m, g, R, and vtop, assuming that the ball is still moving in a circle when it gets there.

b)Find the minimum speed vmin that the ball must have at the top to barely loop the loop (staying on the circular trajectory) with a precisely limp string with tension T = 0 at the top.

c)Determine the speed v0 the ball must have at the bottom to arrive at the top with this minimum speed. You may use either work or potential energy for this part of the problem.

Problem 9.

vmin

R

T m

vo

A ball of mass m is attached to a massless rod (note well) and is suspended from a frictionless pivot. It is moving in a vertical circle of radius R such that it has speed v0 at the bottom as shown. The ball is in a vacuum; neglect drag forces and friction in this problem. Near-Earth gravity acts down.

a)Find an expression for the force exerted on the ball by the rod at the top of the loop as a function of m, g, R, and vtop, assuming that the ball is still moving in a circle when it gets there.

b)Find the minimum speed vmin that the ball must have at the top to barely loop the loop (staying on the circular trajectory). Note that this is easy, once you think about how the rod is di erent from a string!

c)Determine the speed v0 the ball must have at the bottom to arrive at the top with this minimum speed. You may use either work or potential energy for this part of the problem.

Problem 10.

m

H

A block of mass M sits at the top of a frictionless hill of height H. It slides down and around a loop-the-loop of radius R, so that its position on the circle can be identified with the angle θ with respect to the vertical as shown

a)Find the magnitude of the normal force as a function of the angle θ.

b)From this, deduce an expression for the angle θ0 at which the block will leave the track if the block is started at a height H = 2R.

Advanced Problem 11.

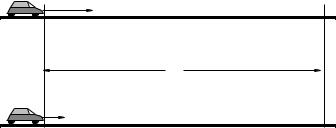
2v0

D

v0

In the figure above we see two cars, one moving at a speed v0 and an identical car moving at a speed 2v0. The cars are moving at a constant speed, so their motors are pushing them forward with a force that precisely cancels the drag force exerted by the air. This drag force is quadratic in their speed:

Fd = −bv2

(in the opposite direction to their velocity) and we assume that this is the only force acting on the car in the direction of motion besides that provided by the motor itself, neglecting various other sources of friction or ine ciency.

a)Prove that the engine of the faster car has to be providing eight times as much power to maintain the higher constant speed than the slower car.

b)Prove that the faster car has to do four times as much work to travel a fixed distance D than the slower car.

Discuss these (very practical) results in your groups. Things you might want to talk over include: Although cars typically do use more gasoline to drive the same distance at 100 kph ( 62 mph) than they do at 50 kph, it isn’t four times as much, or even twice as much. Why not?

Things to think about include gears, engine e ciency, fuel wasted idly, friction, streamlining (dropping to Fd = −bv Stokes’ drag).

Advanced Problem 12.

This is a guided exercise in calculus exploring the kinematics of circular motion and the relation between Cartesian and Plane Polar coordinates. It isn’t as intuitive as the derivation given in the first two weeks, but it is much simpler and is formally correct.

In the figure above, note that:

~r = r cos (θ(t)) xˆ + r sin (θ(t)) yˆ

where r is the radius of the circle and θ(t) is an arbitrary continuous function of time describing where a particle is on the circle at any given time. This is equivalent to:

x(t) = r cos(θ(t))

y(t) = r sin(θ(t))

(going from (r, θ) plane polar coordinates to (x, y) cartesian coordinates and the corresponding:

The first you should already be familiar with as the angular velocity, the second is the angular acceleration. Recall that the tangential speed vt = rω; similarly the tangential acceleration is at = rα as we shall see below.

Work through the following exercises:

a)Find the velocity of the particle ~v in cartesian vector coordinates.

b)Form the dot product ~v · ~r and show that it is zero. This proves that the velocity vector is perpendicular to the radius vector for any particle moving on a circle!

c) Show that the total acceleration of the particle ~a in cartesian vector coordinates can be written as:

Since the direction of ~v results:

(now derived in terms of its cartesian components) and

at = αr.

Optional Problems

The following problems are not required or to be handed in, but are provided to give you some extra things to work on or test yourself with after mastering the required problems and concepts above and to prepare for quizzes and exams.

No optional problems (yet) this week.