
- •Preface
- •Textbook Layout and Design
- •Preliminaries
- •See, Do, Teach
- •Other Conditions for Learning
- •Your Brain and Learning
- •The Method of Three Passes
- •Mathematics
- •Summary
- •Homework for Week 0
- •Summary
- •1.1: Introduction: A Bit of History and Philosophy
- •1.2: Dynamics
- •1.3: Coordinates
- •1.5: Forces
- •1.5.1: The Forces of Nature
- •1.5.2: Force Rules
- •Example 1.6.1: Spring and Mass in Static Force Equilibrium
- •1.7: Simple Motion in One Dimension
- •Example 1.7.1: A Mass Falling from Height H
- •Example 1.7.2: A Constant Force in One Dimension
- •1.7.1: Solving Problems with More Than One Object
- •Example 1.7.4: Braking for Bikes, or Just Breaking Bikes?
- •1.8: Motion in Two Dimensions
- •Example 1.8.1: Trajectory of a Cannonball
- •1.8.2: The Inclined Plane
- •Example 1.8.2: The Inclined Plane
- •1.9: Circular Motion
- •1.9.1: Tangential Velocity
- •1.9.2: Centripetal Acceleration
- •Example 1.9.1: Ball on a String
- •Example 1.9.2: Tether Ball/Conic Pendulum
- •1.9.3: Tangential Acceleration
- •Homework for Week 1
- •Summary
- •2.1: Friction
- •Example 2.1.1: Inclined Plane of Length L with Friction
- •Example 2.1.3: Find The Minimum No-Skid Braking Distance for a Car
- •Example 2.1.4: Car Rounding a Banked Curve with Friction
- •2.2: Drag Forces
- •2.2.1: Stokes, or Laminar Drag
- •2.2.2: Rayleigh, or Turbulent Drag
- •2.2.3: Terminal velocity
- •Example 2.2.1: Falling From a Plane and Surviving
- •2.2.4: Advanced: Solution to Equations of Motion for Turbulent Drag
- •Example 2.2.3: Dropping the Ram
- •2.3.1: Time
- •2.3.2: Space
- •2.4.1: Identifying Inertial Frames
- •Example 2.4.1: Weight in an Elevator
- •Example 2.4.2: Pendulum in a Boxcar
- •2.4.2: Advanced: General Relativity and Accelerating Frames
- •2.5: Just For Fun: Hurricanes
- •Homework for Week 2
- •Week 3: Work and Energy
- •Summary
- •3.1: Work and Kinetic Energy
- •3.1.1: Units of Work and Energy
- •3.1.2: Kinetic Energy
- •3.2: The Work-Kinetic Energy Theorem
- •3.2.1: Derivation I: Rectangle Approximation Summation
- •3.2.2: Derivation II: Calculus-y (Chain Rule) Derivation
- •Example 3.2.1: Pulling a Block
- •Example 3.2.2: Range of a Spring Gun
- •3.3: Conservative Forces: Potential Energy
- •3.3.1: Force from Potential Energy
- •3.3.2: Potential Energy Function for Near-Earth Gravity
- •3.3.3: Springs
- •3.4: Conservation of Mechanical Energy
- •3.4.1: Force, Potential Energy, and Total Mechanical Energy
- •Example 3.4.1: Falling Ball Reprise
- •Example 3.4.2: Block Sliding Down Frictionless Incline Reprise
- •Example 3.4.3: A Simple Pendulum
- •Example 3.4.4: Looping the Loop
- •3.5: Generalized Work-Mechanical Energy Theorem
- •Example 3.5.1: Block Sliding Down a Rough Incline
- •Example 3.5.2: A Spring and Rough Incline
- •3.5.1: Heat and Conservation of Energy
- •3.6: Power
- •Example 3.6.1: Rocket Power
- •3.7: Equilibrium
- •3.7.1: Energy Diagrams: Turning Points and Forbidden Regions
- •Homework for Week 3
- •Summary
- •4.1: Systems of Particles
- •Example 4.1.1: Center of Mass of a Few Discrete Particles
- •4.1.2: Coarse Graining: Continuous Mass Distributions
- •Example 4.1.2: Center of Mass of a Continuous Rod
- •Example 4.1.3: Center of mass of a circular wedge
- •4.2: Momentum
- •4.2.1: The Law of Conservation of Momentum
- •4.3: Impulse
- •Example 4.3.1: Average Force Driving a Golf Ball
- •Example 4.3.2: Force, Impulse and Momentum for Windshield and Bug
- •4.3.1: The Impulse Approximation
- •4.3.2: Impulse, Fluids, and Pressure
- •4.4: Center of Mass Reference Frame
- •4.5: Collisions
- •4.5.1: Momentum Conservation in the Impulse Approximation
- •4.5.2: Elastic Collisions
- •4.5.3: Fully Inelastic Collisions
- •4.5.4: Partially Inelastic Collisions
- •4.6: 1-D Elastic Collisions
- •4.6.1: The Relative Velocity Approach
- •4.6.2: 1D Elastic Collision in the Center of Mass Frame
- •4.7: Elastic Collisions in 2-3 Dimensions
- •4.8: Inelastic Collisions
- •Example 4.8.1: One-dimensional Fully Inelastic Collision (only)
- •Example 4.8.2: Ballistic Pendulum
- •Example 4.8.3: Partially Inelastic Collision
- •4.9: Kinetic Energy in the CM Frame
- •Homework for Week 4
- •Summary
- •5.1: Rotational Coordinates in One Dimension
- •5.2.1: The r-dependence of Torque
- •5.2.2: Summing the Moment of Inertia
- •5.3: The Moment of Inertia
- •Example 5.3.1: The Moment of Inertia of a Rod Pivoted at One End
- •5.3.1: Moment of Inertia of a General Rigid Body
- •Example 5.3.2: Moment of Inertia of a Ring
- •Example 5.3.3: Moment of Inertia of a Disk
- •5.3.2: Table of Useful Moments of Inertia
- •5.4: Torque as a Cross Product
- •Example 5.4.1: Rolling the Spool
- •5.5: Torque and the Center of Gravity
- •Example 5.5.1: The Angular Acceleration of a Hanging Rod
- •Example 5.6.1: A Disk Rolling Down an Incline
- •5.7: Rotational Work and Energy
- •5.7.1: Work Done on a Rigid Object
- •5.7.2: The Rolling Constraint and Work
- •Example 5.7.2: Unrolling Spool
- •Example 5.7.3: A Rolling Ball Loops-the-Loop
- •5.8: The Parallel Axis Theorem
- •Example 5.8.1: Moon Around Earth, Earth Around Sun
- •Example 5.8.2: Moment of Inertia of a Hoop Pivoted on One Side
- •5.9: Perpendicular Axis Theorem
- •Example 5.9.1: Moment of Inertia of Hoop for Planar Axis
- •Homework for Week 5
- •Summary
- •6.1: Vector Torque
- •6.2: Total Torque
- •6.2.1: The Law of Conservation of Angular Momentum
- •Example 6.3.1: Angular Momentum of a Point Mass Moving in a Circle
- •Example 6.3.2: Angular Momentum of a Rod Swinging in a Circle
- •Example 6.3.3: Angular Momentum of a Rotating Disk
- •Example 6.3.4: Angular Momentum of Rod Sweeping out Cone
- •6.4: Angular Momentum Conservation
- •Example 6.4.1: The Spinning Professor
- •6.4.1: Radial Forces and Angular Momentum Conservation
- •Example 6.4.2: Mass Orbits On a String
- •6.5: Collisions
- •Example 6.5.1: Fully Inelastic Collision of Ball of Putty with a Free Rod
- •Example 6.5.2: Fully Inelastic Collision of Ball of Putty with Pivoted Rod
- •6.5.1: More General Collisions
- •Example 6.6.1: Rotating Your Tires
- •6.7: Precession of a Top
- •Homework for Week 6
- •Week 7: Statics
- •Statics Summary
- •7.1: Conditions for Static Equilibrium
- •7.2: Static Equilibrium Problems
- •Example 7.2.1: Balancing a See-Saw
- •Example 7.2.2: Two Saw Horses
- •Example 7.2.3: Hanging a Tavern Sign
- •7.2.1: Equilibrium with a Vector Torque
- •Example 7.2.4: Building a Deck
- •7.3: Tipping
- •Example 7.3.1: Tipping Versus Slipping
- •Example 7.3.2: Tipping While Pushing
- •7.4: Force Couples
- •Example 7.4.1: Rolling the Cylinder Over a Step
- •Homework for Week 7
- •Week 8: Fluids
- •Fluids Summary
- •8.1: General Fluid Properties
- •8.1.1: Pressure
- •8.1.2: Density
- •8.1.3: Compressibility
- •8.1.5: Properties Summary
- •Static Fluids
- •8.1.8: Variation of Pressure in Incompressible Fluids
- •Example 8.1.1: Barometers
- •Example 8.1.2: Variation of Oceanic Pressure with Depth
- •8.1.9: Variation of Pressure in Compressible Fluids
- •Example 8.1.3: Variation of Atmospheric Pressure with Height
- •Example 8.2.1: A Hydraulic Lift
- •8.3: Fluid Displacement and Buoyancy
- •Example 8.3.1: Testing the Crown I
- •Example 8.3.2: Testing the Crown II
- •8.4: Fluid Flow
- •8.4.1: Conservation of Flow
- •Example 8.4.1: Emptying the Iced Tea
- •8.4.3: Fluid Viscosity and Resistance
- •8.4.4: A Brief Note on Turbulence
- •8.5: The Human Circulatory System
- •Example 8.5.1: Atherosclerotic Plaque Partially Occludes a Blood Vessel
- •Example 8.5.2: Aneurisms
- •Homework for Week 8
- •Week 9: Oscillations
- •Oscillation Summary
- •9.1: The Simple Harmonic Oscillator
- •9.1.1: The Archetypical Simple Harmonic Oscillator: A Mass on a Spring
- •9.1.2: The Simple Harmonic Oscillator Solution
- •9.1.3: Plotting the Solution: Relations Involving
- •9.1.4: The Energy of a Mass on a Spring
- •9.2: The Pendulum
- •9.2.1: The Physical Pendulum
- •9.3: Damped Oscillation
- •9.3.1: Properties of the Damped Oscillator
- •Example 9.3.1: Car Shock Absorbers
- •9.4: Damped, Driven Oscillation: Resonance
- •9.4.1: Harmonic Driving Forces
- •9.4.2: Solution to Damped, Driven, Simple Harmonic Oscillator
- •9.5: Elastic Properties of Materials
- •9.5.1: Simple Models for Molecular Bonds
- •9.5.2: The Force Constant
- •9.5.3: A Microscopic Picture of a Solid
- •9.5.4: Shear Forces and the Shear Modulus
- •9.5.5: Deformation and Fracture
- •9.6: Human Bone
- •Example 9.6.1: Scaling of Bones with Animal Size
- •Homework for Week 9
- •Week 10: The Wave Equation
- •Wave Summary
- •10.1: Waves
- •10.2: Waves on a String
- •10.3: Solutions to the Wave Equation
- •10.3.1: An Important Property of Waves: Superposition
- •10.3.2: Arbitrary Waveforms Propagating to the Left or Right
- •10.3.3: Harmonic Waveforms Propagating to the Left or Right
- •10.3.4: Stationary Waves
- •10.5: Energy
- •Homework for Week 10
- •Week 11: Sound
- •Sound Summary
- •11.1: Sound Waves in a Fluid
- •11.2: Sound Wave Solutions
- •11.3: Sound Wave Intensity
- •11.3.1: Sound Displacement and Intensity In Terms of Pressure
- •11.3.2: Sound Pressure and Decibels
- •11.4: Doppler Shift
- •11.4.1: Moving Source
- •11.4.2: Moving Receiver
- •11.4.3: Moving Source and Moving Receiver
- •11.5: Standing Waves in Pipes
- •11.5.1: Pipe Closed at Both Ends
- •11.5.2: Pipe Closed at One End
- •11.5.3: Pipe Open at Both Ends
- •11.6: Beats
- •11.7: Interference and Sound Waves
- •Homework for Week 11
- •Week 12: Gravity
- •Gravity Summary
- •12.1: Cosmological Models
- •12.2.1: Ellipses and Conic Sections
- •12.4: The Gravitational Field
- •12.4.1: Spheres, Shells, General Mass Distributions
- •12.5: Gravitational Potential Energy
- •12.6: Energy Diagrams and Orbits
- •12.7: Escape Velocity, Escape Energy
- •Example 12.7.1: How to Cause an Extinction Event
- •Homework for Week 12

Week 2: Newton’s Laws: Continued |
129 |
2.5: Just For Fun: Hurricanes
Figure 29: Satellite photo of Hurricane Ivan as of September 8, 2004. Note the roughly symmetric rain bands circulating in towards the center and the small but clearly defined “eye”.
Hurricanes are of great interest, at least in the Southeast United States where every fall several of them (on average) make landfall somewhere on the Atlantic or Gulf coast between Texas and North Carolina. Since they not infrequently do billions of dollars worth of damage and kill dozens of people (usually drowned due to flooding) it is worth taking a second to look over their Coriolis dynamics.
In the northern hemisphere, air circulates around high pressure centers in a generally clockwise direction as cool dry air “falls” out of them in all directions, deflecting west as it flows out south and east as it flow out north.
Air circulates around low pressure centers in a counterclockwise direction as air rushes to the center, warms, and lifts. Here the eastward deflection of north-travelling air meets the west deflection of south-travelling air and creates a whirlpool spinning opposite to the far curvature of the incoming air (often flowing in from a circulation pattern around a neighboring high pressure center).
If this circulation occurs over warm ocean water it picks up considerable water vapor and heat. The warm, wet air cools as it lifts in the central pattern of the low and precipitation occurs, releasing the energy of fusion into the rapidly expanding air as wind flowing out of the low pressure center at high altitude in the usual clockwise direction (the “outflow” of the storm). If the low remains over warm ocean water and no “shear” winds blow at high altitude across the developing eye and interfere with the outflow, a stable pattern in the storm emerges that gradually amplifies into a hurricane with a well defined “eye” where the air has very low pressure and no wind at all.
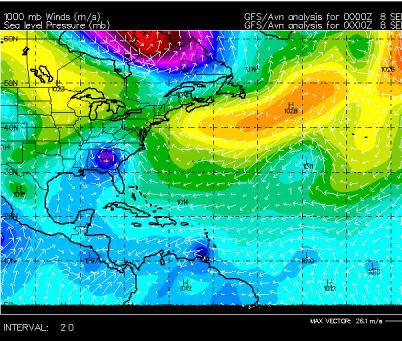
Figure 32 shows a “snapshot” of the high and low pressure centers over much of North and South America and the Atlantic on September 8, 2004. In it, two “extreme low” pressure centers are clearly visible that are either hurricanes or hurricane remnants. Note well the counterclockwise circulation around these lows. Two large high pressure regions are also clearly visible, with air circulating around them (irregularly) clockwise. This rotation smoothly transitions into the rotation around the lows across boundary regions.

130 |
Week 2: Newton’s Laws: Continued |
(North−−Counter Clockwise)
Hurricane
N
Eye
Southward trajectory
North to South deflects west
direction of rotation
Falling deflects east
 S
S
Figure 30:
Figure 31: Coriolis dynamics associated with tropical storms. Air circulating clockwise (from surrounding higher pressure regions) meets at a center of low pressure and forms a counterclockwise “eye”.
As you can see the dynamics of all of this are rather complicated – air cannot just “flow” on the surface of the Earth – it has to flow from one place to another, being replaced as it flows. As it flows north and south, east and west, up and down, pseudoforces associated with the Earth’s rotation join the real forces of gravitation, air pressure di erences, buoyancy associated with di erential heating and cooling due to insolation, radiation losses, conduction and convection, and moisture accumulation and release, and more. Atmospheric modelling is di cult and not terribly skilled (predictive) beyond around a week or at most two, at which point small fluctuations in the initial conditions often grow to unexpectedly dominate global weather patterns, the so-called “butterfly e ect”76 .
In the specific case of hurricanes (that do a lot of damage, providing a lot of political and economic incentive to improve the predictive models) the details of the dynamics and energy release are only gradually being understood by virtue of intense study, and at this point the hurricane models are quite good at predicting motion and consequence within reasonable error bars up to five or six days in advance. There is a wealth of information available on the Internet77 to any who wish to learn more. An article78 on the Atlantic Oceanographic and Meteorological Laboratory’s Hurricane Frequently Asked Questions79 website contains a lovely description of the structure of the eye and the inflowing rain bands.
Atlantic hurricanes usually move from Southeast to Northwest in the Atlantic North of the
76Wikipedia: http://www.wikipedia.org/wiki/Butterfly E ect. So named because “The flap of a butterfly’s wings in Brazil causes a hurricane in the U.S. some months later.” This latter sort of statement isn’t really correct, of course – many things conspire to cause the hurricane. It is intended to reflect the fact that weather systems exhibit deterministic chaotic dynamics – infinite sensitivity to initial conditions so that tiny di erences in initial state lead to radically di erent states later on.
77Wikipedia: http://www.wikipedia.org/wiki/Tropical Cyclone.
78http://www.aoml.noaa.gov/hrd/tcfaq/A11.html
79http://www.aoml.noaa.gov/hrd/weather sub/faq.html
Week 2: Newton’s Laws: Continued |
131 |
Figure 32: Pressure/windfield of the Atlantic on September 8, 2004. Two tropical storms are visible
– the remnants of Hurricane Frances poised over the U.S. Southeast, and Hurricane Ivan just north of South America. Two more low pressure “tropical waves” are visible between South America and Africa – either or both could develop into tropical storms if shear and water temperature are favorable. The low pressure system in the middle of the Atlantic is extratropical and very unlikely to develop into a proper tropical storm.
equator until they hook away to the North or Northeast. Often they sweep away into the North Atlantic to die as mere extratropical storms without ever touching land. When they do come ashore, though, they can pack winds well over a hundred miles an hour. This is faster than the “terminal velocity” associated with atmospheric drag and thereby they are powerful enough to lift a human or a cow right o their feet, or a house right o its foundations. In addition, even mere “tropical storms” (which typically have winds in the range where wind per se does relatively little damage) can drop a foot of rain in a matter of hours across tens of thousands of square miles or spin down local tornadoes with high and damaging winds. Massive flooding, not wind, is the most common cause of loss of life in hurricanes and other tropical storms.
Hurricanes also can form in the Gulf of Mexico, the Carribean, or even the waters of the Pacific close to Mexico. Tropical cyclones in general occur in all of the world’s tropical oceans except for the Atlantic south of the equator, with the highest density of occurrence in the Western Pacific (where they are usually called “typhoons” instead of “hurricanes”). All hurricanes tend to be highly unpredictable in their behavior as they bounce around between and around surrounding air pressure ridges and troughs like a pinball in a pinball machine, and even the best of computational models, updated regularly as the hurricane evolves, often err by over 100 kilometers over the course of just a day or two.
132 |
Week 2: Newton’s Laws: Continued |
Homework for Week 2
Problem 1.
Physics Concepts: Make this week’s physics concepts summary as you work all of the problems in this week’s assignment. Be sure to cross-reference each concept in the summary to the problem(s) they were key to, and include concepts from previous weeks as necessary. Do the work carefully enough that you can (after it has been handed in and graded) punch it and add it to a three ring binder for review and study come finals!
Problem 2.
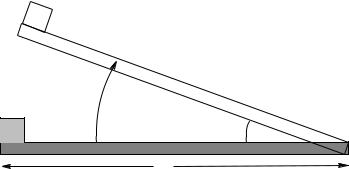
m |
θ |
|
|
|
L |
A block of mass m sits at rest on a rough plank of length L that can be gradually tipped up until the block slides. The coe cient of static friction between the block and the plank is µs; the coe cient of dynamic friction is µk and as usual, µk < µs.
a)Find the angle θ0 at which the block first starts to move.
b)Suppose that the plank is lifted to an angle θ > θ0 (where the mass will definitely slide) and the mass is released from rest at time t0 = 0. Find its acceleration a down the incline.
c)Finally, find the time tf that the mass reaches the lower end of the plank.

Week 2: Newton’s Laws: Continued |
133 |
Problem 3.
m1 r
v 
m2 
A hockey puck of mass m1 is tied to a string that passes through a hole in a frictionless table, where it is also attached to a mass m2 that hangs underneath. The mass is given a push so that it moves in a circle of radius r at constant speed v when mass m2 hangs free beneath the table. Find r as a function of m1, m2, v, and g.
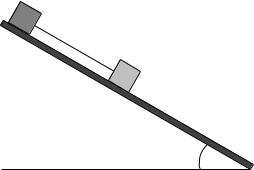
Problem 4.
θ
m
F
M
A small square block m is sitting on a larger wedge-shaped block of mass M at an upper angle θ0 such that the little block will slide on the big block if both are started from rest and no other forces are present. The large block is sitting on a frictionless table. The coe cient of static friction between the large and small blocks is µs. With what range of force F can you push on the large block to the right such that the small block will remain motionless with respect to the large block and neither slide up nor slide down?

134 |
Week 2: Newton’s Laws: Continued |
Problem 5.
m1
m 2
A mass m1 is attached to a second mass m2 by an Acme (massless, unstretchable) string. m1 sits on a table with which it has coe cients of static and dynamic friction µs and µk respectively. m2 is hanging over the ends of a table, suspended by the taut string from an Acme (frictionless, massless) pulley. At time t = 0 both masses are released.
a)What is the minimum mass m2,min such that the two masses begin to move?
b)If m2 = 2m2,min, determine how fast the two blocks are moving when mass m2 has fallen a height H (assuming that m1 hasn’t yet hit the pulley)?
Problem 6.
v |
m |
towards center |
R |
θ |
|
(top view) |
(side view) |
A car of mass m is rounding a banked curve that has radius of curvature R and banking angle θ. Find the speed v of the car such that it succeeds in making it around the curve without skidding on an extremely icy day when µs ≈ 0.

Week 2: Newton’s Laws: Continued |
135 |
Problem 7.
v |
m |
towards center |
R |
θ |
|
(top view) |
(side view) |
A car of mass m is rounding a banked curve that has radius of curvature R and banking angle θ. The coe cient of static friction between the car’s tires and the road is µs. Find the range of speeds v of the car such that it can succeed in making it around the curve without skidding.
Problem 8.
v
m
You and a friend are working inside a cylindrical new space station that is a hundred meters long and thirty meters in radius and filled with a thick air mixture. It is lunchtime and you have a bag of oranges. Your friend (working at the other end of the cylinder) wants one, so you throw one at him
~
at speed v0 at t = 0. Assume Stokes drag, that is F d = −b~v (this is probably a poor assumption depending on the initial speed, but it makes the algebra relatively easy and qualitatively describes the motion well enough).
a)Derive an algebraic expression for the velocity of the orange as a function of time.
b)How long does it take the orange to lose half of its initial velocity?
136 |
Week 2: Newton’s Laws: Continued |
Problem 9.
R
m v
A bead of mass m is threaded on a metal hoop of radius R. There is a coe cient of kinetic friction µk between the bead and the hoop. It is given a push to start it sliding around the hoop with initial speed v0. The hoop is located on the space station, so you can ignore gravity.
a)Find the normal force exerted by the hoop on the bead as a function of its speed.
b)Find the dynamical frictional force exerted by the hoop on the bead as a function of its speed.
c)Find its speed as a function of time. This involves using the frictional force on the bead in Newton’s second law, finding its tangential acceleration on the hoop (which is the time rate of change of its speed) and solving the equation of motion.
All answers should be given in terms of m, µk, R, v (where requested) and v0.

Week 2: Newton’s Laws: Continued |
137 |
Problem 10.
m2
m1
A block of mass m2 sits on a rough table. The coe cients of friction between the block and the table are µs and µk for static and kinetic friction respectively. A mass m1 is suspended from an massless, unstretchable, unbreakable rope that is looped around the two pulleys as shown and attached to the support of the rightmost pulley. At time t = 0 the system is released at rest.
a)Find an expression for the minimum mass m1,min such that the masses will begin to move.
b)Suppose m1 = 2m1,min (twice as large as necessary to start it moving). Solve for the accelerations of both masses. Hint: Is there a constraint between how far mass m2 moves when mass m1 moves down a short distance?
c)Find the speed of both masses after the small mass has fallen a distance H. Remember this answer and how hard you had to work to find it – next week we will find it much more easily.
138 |
Week 2: Newton’s Laws: Continued |
Problem 11.
1
m
2
m
θ
Two blocks, each with the same mass m but made of di erent materials, sit on a rough plane inclined at an angle θ such that they will slide (so that the component of their weight down the incline exceeds the maximum force exerted by static friction). The first (upper) block has a coe cient of kinetic friction of µk1 between block and inclined plane; the second (lower) block has coe cient of kinetic friction µk2. The two blocks are connected by an Acme string.
Find the acceleration of the two blocks a1 and a2 down the incline:
a)when µk1 > µk2;
b)when µk2 > µk1.
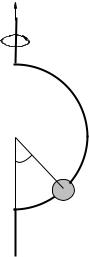
Week 2: Newton’s Laws: Continued |
139 |
Advanced Problem 12.
ω
θR
m
A small frictionless bead is threaded on a semicircular wire hoop with radius R, which is then spun on its vertical axis as shown above at angular velocity ω.
a)Find an expression for θ in terms of R, g and ω.
b)What is the smallest angular frequency ωmin such that the bead will not sit at the bottom at θ = 0, for a given R.
140 |
Week 3: Work and Energy |
Optional Problems
The following problems are not required or to be handed in, but are provided to give you some extra things to work on or test yourself with after mastering the required problems and concepts above and to prepare for quizzes and exams.
No optional problems (yet) this week.
