
- •Preface
- •Textbook Layout and Design
- •Preliminaries
- •See, Do, Teach
- •Other Conditions for Learning
- •Your Brain and Learning
- •The Method of Three Passes
- •Mathematics
- •Summary
- •Homework for Week 0
- •Summary
- •1.1: Introduction: A Bit of History and Philosophy
- •1.2: Dynamics
- •1.3: Coordinates
- •1.5: Forces
- •1.5.1: The Forces of Nature
- •1.5.2: Force Rules
- •Example 1.6.1: Spring and Mass in Static Force Equilibrium
- •1.7: Simple Motion in One Dimension
- •Example 1.7.1: A Mass Falling from Height H
- •Example 1.7.2: A Constant Force in One Dimension
- •1.7.1: Solving Problems with More Than One Object
- •Example 1.7.4: Braking for Bikes, or Just Breaking Bikes?
- •1.8: Motion in Two Dimensions
- •Example 1.8.1: Trajectory of a Cannonball
- •1.8.2: The Inclined Plane
- •Example 1.8.2: The Inclined Plane
- •1.9: Circular Motion
- •1.9.1: Tangential Velocity
- •1.9.2: Centripetal Acceleration
- •Example 1.9.1: Ball on a String
- •Example 1.9.2: Tether Ball/Conic Pendulum
- •1.9.3: Tangential Acceleration
- •Homework for Week 1
- •Summary
- •2.1: Friction
- •Example 2.1.1: Inclined Plane of Length L with Friction
- •Example 2.1.3: Find The Minimum No-Skid Braking Distance for a Car
- •Example 2.1.4: Car Rounding a Banked Curve with Friction
- •2.2: Drag Forces
- •2.2.1: Stokes, or Laminar Drag
- •2.2.2: Rayleigh, or Turbulent Drag
- •2.2.3: Terminal velocity
- •Example 2.2.1: Falling From a Plane and Surviving
- •2.2.4: Advanced: Solution to Equations of Motion for Turbulent Drag
- •Example 2.2.3: Dropping the Ram
- •2.3.1: Time
- •2.3.2: Space
- •2.4.1: Identifying Inertial Frames
- •Example 2.4.1: Weight in an Elevator
- •Example 2.4.2: Pendulum in a Boxcar
- •2.4.2: Advanced: General Relativity and Accelerating Frames
- •2.5: Just For Fun: Hurricanes
- •Homework for Week 2
- •Week 3: Work and Energy
- •Summary
- •3.1: Work and Kinetic Energy
- •3.1.1: Units of Work and Energy
- •3.1.2: Kinetic Energy
- •3.2: The Work-Kinetic Energy Theorem
- •3.2.1: Derivation I: Rectangle Approximation Summation
- •3.2.2: Derivation II: Calculus-y (Chain Rule) Derivation
- •Example 3.2.1: Pulling a Block
- •Example 3.2.2: Range of a Spring Gun
- •3.3: Conservative Forces: Potential Energy
- •3.3.1: Force from Potential Energy
- •3.3.2: Potential Energy Function for Near-Earth Gravity
- •3.3.3: Springs
- •3.4: Conservation of Mechanical Energy
- •3.4.1: Force, Potential Energy, and Total Mechanical Energy
- •Example 3.4.1: Falling Ball Reprise
- •Example 3.4.2: Block Sliding Down Frictionless Incline Reprise
- •Example 3.4.3: A Simple Pendulum
- •Example 3.4.4: Looping the Loop
- •3.5: Generalized Work-Mechanical Energy Theorem
- •Example 3.5.1: Block Sliding Down a Rough Incline
- •Example 3.5.2: A Spring and Rough Incline
- •3.5.1: Heat and Conservation of Energy
- •3.6: Power
- •Example 3.6.1: Rocket Power
- •3.7: Equilibrium
- •3.7.1: Energy Diagrams: Turning Points and Forbidden Regions
- •Homework for Week 3
- •Summary
- •4.1: Systems of Particles
- •Example 4.1.1: Center of Mass of a Few Discrete Particles
- •4.1.2: Coarse Graining: Continuous Mass Distributions
- •Example 4.1.2: Center of Mass of a Continuous Rod
- •Example 4.1.3: Center of mass of a circular wedge
- •4.2: Momentum
- •4.2.1: The Law of Conservation of Momentum
- •4.3: Impulse
- •Example 4.3.1: Average Force Driving a Golf Ball
- •Example 4.3.2: Force, Impulse and Momentum for Windshield and Bug
- •4.3.1: The Impulse Approximation
- •4.3.2: Impulse, Fluids, and Pressure
- •4.4: Center of Mass Reference Frame
- •4.5: Collisions
- •4.5.1: Momentum Conservation in the Impulse Approximation
- •4.5.2: Elastic Collisions
- •4.5.3: Fully Inelastic Collisions
- •4.5.4: Partially Inelastic Collisions
- •4.6: 1-D Elastic Collisions
- •4.6.1: The Relative Velocity Approach
- •4.6.2: 1D Elastic Collision in the Center of Mass Frame
- •4.7: Elastic Collisions in 2-3 Dimensions
- •4.8: Inelastic Collisions
- •Example 4.8.1: One-dimensional Fully Inelastic Collision (only)
- •Example 4.8.2: Ballistic Pendulum
- •Example 4.8.3: Partially Inelastic Collision
- •4.9: Kinetic Energy in the CM Frame
- •Homework for Week 4
- •Summary
- •5.1: Rotational Coordinates in One Dimension
- •5.2.1: The r-dependence of Torque
- •5.2.2: Summing the Moment of Inertia
- •5.3: The Moment of Inertia
- •Example 5.3.1: The Moment of Inertia of a Rod Pivoted at One End
- •5.3.1: Moment of Inertia of a General Rigid Body
- •Example 5.3.2: Moment of Inertia of a Ring
- •Example 5.3.3: Moment of Inertia of a Disk
- •5.3.2: Table of Useful Moments of Inertia
- •5.4: Torque as a Cross Product
- •Example 5.4.1: Rolling the Spool
- •5.5: Torque and the Center of Gravity
- •Example 5.5.1: The Angular Acceleration of a Hanging Rod
- •Example 5.6.1: A Disk Rolling Down an Incline
- •5.7: Rotational Work and Energy
- •5.7.1: Work Done on a Rigid Object
- •5.7.2: The Rolling Constraint and Work
- •Example 5.7.2: Unrolling Spool
- •Example 5.7.3: A Rolling Ball Loops-the-Loop
- •5.8: The Parallel Axis Theorem
- •Example 5.8.1: Moon Around Earth, Earth Around Sun
- •Example 5.8.2: Moment of Inertia of a Hoop Pivoted on One Side
- •5.9: Perpendicular Axis Theorem
- •Example 5.9.1: Moment of Inertia of Hoop for Planar Axis
- •Homework for Week 5
- •Summary
- •6.1: Vector Torque
- •6.2: Total Torque
- •6.2.1: The Law of Conservation of Angular Momentum
- •Example 6.3.1: Angular Momentum of a Point Mass Moving in a Circle
- •Example 6.3.2: Angular Momentum of a Rod Swinging in a Circle
- •Example 6.3.3: Angular Momentum of a Rotating Disk
- •Example 6.3.4: Angular Momentum of Rod Sweeping out Cone
- •6.4: Angular Momentum Conservation
- •Example 6.4.1: The Spinning Professor
- •6.4.1: Radial Forces and Angular Momentum Conservation
- •Example 6.4.2: Mass Orbits On a String
- •6.5: Collisions
- •Example 6.5.1: Fully Inelastic Collision of Ball of Putty with a Free Rod
- •Example 6.5.2: Fully Inelastic Collision of Ball of Putty with Pivoted Rod
- •6.5.1: More General Collisions
- •Example 6.6.1: Rotating Your Tires
- •6.7: Precession of a Top
- •Homework for Week 6
- •Week 7: Statics
- •Statics Summary
- •7.1: Conditions for Static Equilibrium
- •7.2: Static Equilibrium Problems
- •Example 7.2.1: Balancing a See-Saw
- •Example 7.2.2: Two Saw Horses
- •Example 7.2.3: Hanging a Tavern Sign
- •7.2.1: Equilibrium with a Vector Torque
- •Example 7.2.4: Building a Deck
- •7.3: Tipping
- •Example 7.3.1: Tipping Versus Slipping
- •Example 7.3.2: Tipping While Pushing
- •7.4: Force Couples
- •Example 7.4.1: Rolling the Cylinder Over a Step
- •Homework for Week 7
- •Week 8: Fluids
- •Fluids Summary
- •8.1: General Fluid Properties
- •8.1.1: Pressure
- •8.1.2: Density
- •8.1.3: Compressibility
- •8.1.5: Properties Summary
- •Static Fluids
- •8.1.8: Variation of Pressure in Incompressible Fluids
- •Example 8.1.1: Barometers
- •Example 8.1.2: Variation of Oceanic Pressure with Depth
- •8.1.9: Variation of Pressure in Compressible Fluids
- •Example 8.1.3: Variation of Atmospheric Pressure with Height
- •Example 8.2.1: A Hydraulic Lift
- •8.3: Fluid Displacement and Buoyancy
- •Example 8.3.1: Testing the Crown I
- •Example 8.3.2: Testing the Crown II
- •8.4: Fluid Flow
- •8.4.1: Conservation of Flow
- •Example 8.4.1: Emptying the Iced Tea
- •8.4.3: Fluid Viscosity and Resistance
- •8.4.4: A Brief Note on Turbulence
- •8.5: The Human Circulatory System
- •Example 8.5.1: Atherosclerotic Plaque Partially Occludes a Blood Vessel
- •Example 8.5.2: Aneurisms
- •Homework for Week 8
- •Week 9: Oscillations
- •Oscillation Summary
- •9.1: The Simple Harmonic Oscillator
- •9.1.1: The Archetypical Simple Harmonic Oscillator: A Mass on a Spring
- •9.1.2: The Simple Harmonic Oscillator Solution
- •9.1.3: Plotting the Solution: Relations Involving
- •9.1.4: The Energy of a Mass on a Spring
- •9.2: The Pendulum
- •9.2.1: The Physical Pendulum
- •9.3: Damped Oscillation
- •9.3.1: Properties of the Damped Oscillator
- •Example 9.3.1: Car Shock Absorbers
- •9.4: Damped, Driven Oscillation: Resonance
- •9.4.1: Harmonic Driving Forces
- •9.4.2: Solution to Damped, Driven, Simple Harmonic Oscillator
- •9.5: Elastic Properties of Materials
- •9.5.1: Simple Models for Molecular Bonds
- •9.5.2: The Force Constant
- •9.5.3: A Microscopic Picture of a Solid
- •9.5.4: Shear Forces and the Shear Modulus
- •9.5.5: Deformation and Fracture
- •9.6: Human Bone
- •Example 9.6.1: Scaling of Bones with Animal Size
- •Homework for Week 9
- •Week 10: The Wave Equation
- •Wave Summary
- •10.1: Waves
- •10.2: Waves on a String
- •10.3: Solutions to the Wave Equation
- •10.3.1: An Important Property of Waves: Superposition
- •10.3.2: Arbitrary Waveforms Propagating to the Left or Right
- •10.3.3: Harmonic Waveforms Propagating to the Left or Right
- •10.3.4: Stationary Waves
- •10.5: Energy
- •Homework for Week 10
- •Week 11: Sound
- •Sound Summary
- •11.1: Sound Waves in a Fluid
- •11.2: Sound Wave Solutions
- •11.3: Sound Wave Intensity
- •11.3.1: Sound Displacement and Intensity In Terms of Pressure
- •11.3.2: Sound Pressure and Decibels
- •11.4: Doppler Shift
- •11.4.1: Moving Source
- •11.4.2: Moving Receiver
- •11.4.3: Moving Source and Moving Receiver
- •11.5: Standing Waves in Pipes
- •11.5.1: Pipe Closed at Both Ends
- •11.5.2: Pipe Closed at One End
- •11.5.3: Pipe Open at Both Ends
- •11.6: Beats
- •11.7: Interference and Sound Waves
- •Homework for Week 11
- •Week 12: Gravity
- •Gravity Summary
- •12.1: Cosmological Models
- •12.2.1: Ellipses and Conic Sections
- •12.4: The Gravitational Field
- •12.4.1: Spheres, Shells, General Mass Distributions
- •12.5: Gravitational Potential Energy
- •12.6: Energy Diagrams and Orbits
- •12.7: Escape Velocity, Escape Energy
- •Example 12.7.1: How to Cause an Extinction Event
- •Homework for Week 12

58 |
Week 1: Newton’s Laws |
kind of motion does the overall solution describe, on the interval from t = (−∞, ∞)? Do we need to use a certain amount of common sense to avoid using the algebraic solution for times or values of y for which they make no sense, such as y < 0 or t < 0 (in the ground or before we let go of the ball, respectively)?
The last thing we might look at I’m going to let you do on your own (don’t worry, it’s easy enough to do in your head). Assuming that this algebraic solution is valid for any reasonable H, how fast does the ball hit the ground after falling (say) 5 meters? How about 20 = 4 5 meters? How about 80 = 16 5 meters? How long does it take for the ball to fall 5 meters, 20 meters, 80 meters, etc? In this course we won’t do a lot of arithmetic, but whenever we learn a new idea with parameters like g in it, it is useful to do a little arithmetical exploration to see what a “reasonable” answer looks like. Especially note how the answers scale with the height – if one drops it from 4x the height, how much does that increase the time it falls and speed with which it hits?
One of these heights causes it to hit the ground in one second, and all of the other answers scale with it like the square root. If you happen to remember this height, you can actually estimate how long it takes for a ball to fall almost any height in your head with a division and a square root, and if you multiply the time answer by ten, well, there is the speed with which it hits! We’ll do some conceptual problems that help you understand this scaling idea for homework.
This (a falling object) is nearly a perfect problem archetype or example for one dimensional motion. Sure, we can make it more complicated, but usually we’ll do that by having more than one thing move in one dimension and then have to figure out how to solve the two problems simultaneously and answer questions given the results.
Let’s take a short break to formally solve the equation of motion we get for a constant force in one dimension, as the general solution exhibits two constants of integration that we need to be able to identify and evaluate from initial conditions. Note well that the next problem is almost identical
~
to the former one. It just di ers in that you are given the force F itself, not a knowledge that the force is e.g. “gravity”.
Example 1.7.2: A Constant Force in One Dimension
This time we’ll imagine a di erent problem. A car of mass m is travelling at a constant speed v0 as it enters a long, nearly straight merge lane. A distance d from the entrance, the driver presses the accelerator and the engine exerts a constant force of magnitude F on the car.
a)How long does it take the car to reach a final velocity vf > v0?
b)How far (from the entrance) does it travel in that time?
As before, we need to start with a good picture of what is going on. Hence a car:
|
y |
|
|
|
|
|
t = 0 |
|
t = t f |
m |
v |
v0 |
F |
v |
|
0 |
|
f |
|
|
|
|
x |
d |
D |
Figure 6: One possible way to portray the motion of the car and coordinatize it.
Week 1: Newton’s Laws |
59 |
In figure 6 we see what we can imagine are three “slices” of the car’s position as a function of time at the moments described in the problem. On the far left we see it “entering a long, nearly straight merge lane”. The second position corresponds to the time the car is a distance d from the entrance, which is also the time the car starts to accelerate because of the force F . I chose to start the clock then, so that I can integrate to find the position as a function of time while the force is being applied. The final position corresponds to when the car has had the force applied for a time tf and has acquired a velocity vf . I labelled the distance of the car from the entrance D at that time. The mass of the car is indicated as well.
This figure completely captures the important features of the problem! Well, almost. There are two forces I ignored altogether. One of them is gravity, which is pulling the car down. The other is the so-called normal force exerted by the road on the car – this force pushes the car up. I ignored them because my experience and common sense tell me that under ordinary circumstances the road doesn’t push on the car so that it jumps into the air, nor does gravity pull the car down into the road
– the two forces will balance and the car will not move or accelerate in the vertical direction. Next week we’ll take these forces into explicit account too, but here I’m just going to use my intuition that they will cancel and hence that the y-direction can be ignored, all of the motion is going to be in the x-direction as I’ve defined it with my coordinate axes.
It’s time to follow our ritual. We will write Newton’s Second Law and solve for the acceleration (obtaining an equation of motion). Then we will integrate twice to find first vx(t) and then x(t). We will have to be extra careful with the constants of integration this time, and in fact will get a very general solution, one that can be applied to all constant acceleration problems, although I do not recommend that you memorize this solution and try to use it every time you see Newton’s Second Law! For one thing, we’ll have quite a few problems this year where the force, and acceleration, are not constant and in those problems the solution we will derive is wrong. Alas, to my own extensive and direct experience, students that memorize kinematic solutions to the constant acceleration problem instead of learning to solve it with actual integration done every time almost invariably try applying the solution to e.g. the harmonic oscillator problem later, and I hate that. So don’t memorize the answer; learn how to derive it and practice the derivation until (sure) you know the result, and also know when you can use it.
Thus:
F= max
ax = |
|
F |
= a0 |
(a constant) |
|
|
|
||||
m |
|||||
dvx |
= |
a0 |
|
(50) |
|
dt |
|
||||
|
|
|
|
|
|
Next, multiply through by dt and integrate both sides:
vx(t) = Z |
dvx = Z |
a0 |
dt = a0t + V = m t + V |
(51) |
|
|
|
|
|
F |
|
Either of the last two are valid answers, provided that we define a0 = F/m somewhere in the solution and also provided that the problem doesn’t explicitly ask for an answer to be given in terms of F and m. V is a constant of integration that we will evaluate below.
Note that if a0 = F/m was not a constant (say that F(t) is a function of time) then we would have to do the integral :
vx(t) = |
Z Fm |
dt = m Z |
F (t) dt =??? |
(52) |
||
|
|
(t) |
1 |
|
|
|
At the very least, we would have to know the explicit functional form of F (t) to proceed, and the answer would not be linear in time.

60 Week 1: Newton’s Laws
At time t = 0, the velocity of the car in the x-direction is v0, so (check for yourself) V = v0 and:
vx(t) = a0t + v0 = |
dx |
(53) |
dt |
We multiply this equation by dt on both sides, integrate, and get:
x(t) = Z |
dx = Z |
(a0t + v0) dt = 2 a0t2 |
+ v0t + x0 |
(54) |
|
|
|
1 |
|
|
|
where x0 is the constant of integration. We note that at time t = 0, x(0) = d, so x0 = d. Thus:
x(t) = |
1 |
a0t2 |
+ v0t + d |
(55) |
|
2 |
|||||
|
|
|
|
It is worth collecting the two basic solutions in one place. It should be obvious that for any one-dimensional (say, in the x-direction) constant acceleration ax = a0 problem we will always find that:
vx(t) |
= |
a0t + v0 |
(56) |
||||
x(t) |
= |
|
1 |
a0t2 |
+ v0t + x0 |
(57) |
|
2 |
|||||||
|
|
|
|
|
|||
where x0 is the x-position at time t = 0 and v0 is the x-velocity at time t = 0. You can see why it is so very tempting to just memorize this result and pretend that you know a piece of physics, but don’t!
The algebra that led to this answer is basically ordinary math with units. As we’ve seen, “math with units” has a special name all its own – kinematics – and the pair of equations 56 and 57 are called the kinematic solutions to the constant acceleration problem. Kinematics should be contrasted with dynamics, the physics of forces and laws of nature that lead us to equations of motion. One way of viewing our solution strategy is that – after drawing and decorating our figure, of course – we solve first the dynamics problem of writing our dynamical principle (Newton’s Second Law with the appropriate vector total force), turning it into a di erential equation of motion, then solving the resulting kinematics problem represented by the equation of motion with calculus. Don’t be tempted to skip the calculus and try to memorize the kinematic solutions – it is just as important to understand and be able to do the kinematic calculus quickly and painlessly as it is to be able to set up the dynamical part of the solution.
Now, of course, we have to actually answer the questions given above. To do this requires as before logic, common sense, intuition, experience, and math. First, at what time tf does the car have speed vf ? When:
vx(tf ) = vf = a0tf + v0 |
(58) |
of course. You can easily solve this for tf . Note that I just transformed the English statement “At tf , the car must have speed vf ” into an algebraic equation that means the exact same thing!
Second, what is D? Well in English, the distance D from the entrance is where the car is at time tf , when it is also travelling at speed vf . If we turn this sentence into an equation we get:
x(t |
) = D = |
1 |
a t2 |
+ v |
t |
|
+ d |
(59) |
|
|
|||||||
f |
|
2 0 f |
0 |
|
f |
|
|
|
Again, having solved the previous equation algebraically, you can substitute the result for tf into this equation and get D in terms of the originally given quantities! The problem is solved, the questions are answered, we’re finished.
Or rather, you will be finished, after you fill in these last couple of steps on your own!
Week 1: Newton’s Laws |
61 |
1.7.1: Solving Problems with More Than One Object
One of the keys to answering the questions in both of these examples has been turning easy-enough statements in English into equations, and then solving the equations to obtain an answer to a question also framed in English. So far, we have solved only single equations, but we will often be working with more than one thing at a time, or combining two or more principles, so that we have to solve several simultaneous equations.
The only change we might make to our existing solution strategy is to construct and solve the equations of motion for each object or independent aspect (such as dimension) of the problem. In a moment, we’ll consider problems of the latter sort, where this strategy will work when the force in one coordinate direction is independent of the force in another coordinate direction! . First, though, let’s do a couple of very simple one-dimensional problems with two objects with some sort of constraint connecting the motion of one to the motion of the other.
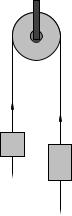
Example 1.7.3: Atwood’s Machine
T
T
m1
m2
 m 1 g
m 1 g
 m 2 g
m 2 g
Figure 7: Atwood’s Machines consists of a pair of masses (usually of di erent mass) connected by a string that runs over a pulley as shown. Initially we idealize by considering the pulley to be massless and frictionless, the string to be massless and unstretchable, and ignore drag forces.
A mass m1 and a second mass m2 are hung at both ends of a massless, unstretchable string that runs over a frictionless, massless pulley as shown in figure 7. Gravity near the Earth’s surface pulls both down. Assuming that the masses are released from rest at time t = 0, find:
a)The acceleration of both masses;
b)The tension T in the string;
c)The speed of the masses after they have moved through a distance H in the direction of the more massive one.
The trick of this problem is to note that if mass m2 goes down by a distance (say) x, mass m1 goes up by the same distance x and vice versa. The magnitude of the displacement of one is the same as that of the other, as they are connected by a taut unstretchable string. This also means that the speed of one rising equals the speed of the other falling, the magnitude of the acceleration of one up equals the magnitude of the acceleration of the other down. So even though it at first looks like you need two coordinate systems for this problem, x1 (measured from m1’s initial position, up or down) will equal x2 (measured from m2’s initial position, down or up) be the same. We therefore
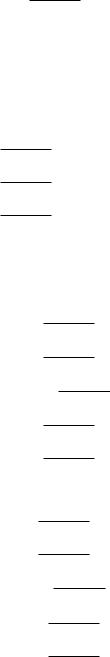
62 Week 1: Newton’s Laws
can just use x to describe this displacement (the displacement of m1 up and m2 down from its starting position), with vx and ax being the same for both masses with the same convention.
This, then, is a wraparound one-dimensional coordinate system, one that “curves around the pulley”. In these coordinates, Newton’s Second Law for the two masses becomes the two equations:
F1 |
= |
T − m1g = m1ax |
(60) |
F2 |
= |
m2g − T = m2ax |
(61) |
This is a set of two equations and two unknowns (T and ax). It is easiest to solve by elimination.
If we add the two equations we eliminate T and get: |
|
||||
m2g − m1g = (m2 − m1)g = m1ax + m2ax = (m1 + m2)ax |
(62) |
||||
or |
|
|
|
||
ax = |
m2 |
− m1 |
g |
(63) |
|
m1 |
|||||
|
+ m2 |
|
|||
In the figure above, if m2 > m1 (as the figure suggests) then both mass m2 will accelerate down and m1 will accelerate up with this constant acceleration.
We can find T by substituting this value for ax into either force equation:
T − m1g = |
m1ax |
|
|
|
|
|||||
T |
− |
m |
g = |
|
m2 − m1 |
m |
g |
|||
|
1 |
|
|
m1 + m2 |
1 |
|
|
|
||
|
|
T = |
|
m2 − m1 |
m1g + m1g |
|||||
|
|
|
|
|
m1 + m2 |
|
|
|
|
|
|
|
T = |
|
m2 − m1 |
m1g + |
m2 + m1 |
m1g |
|||
|
|
|
|
|
||||||
|
|
|
|
|
m1 + m2 |
|
|
m1 + m2 |
||
|
|
T = |
|
2m2m1 |
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
m1 + m2 |
|
|
|
|
|
ax is constant, so we can evaluate vx(t) and x(t) exactly as we did for a falling ball:
ax = |
dvx |
|
= |
|
|
m2 − m1 |
g |
||||||||||||
|
dt |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
m1 + m2 |
||||||||||||||
|
|
|
dvx |
= |
|
|
m2 − m1 |
g dt |
|||||||||||
Z |
|
|
|
|
|
|
|
m1 + m2 |
|||||||||||
|
|
|
x |
|
|
Z |
m1 |
+ m2 |
|||||||||||
|
|
|
dv |
|
|
= |
|
|
|
|
|
m2 |
− m1 |
g dt |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
vx |
= |
|
|
m2 − m1 |
gt + C |
|||||||||||
|
|
|
|
|
|
|
|
m1 + m2 |
|||||||||||
|
vx(t) = |
|
|
m2 − m1 |
gt |
||||||||||||||
|
|
|
|
|
|
|
|
m1 + m2 |
|||||||||||
and then: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
vx(t) = |
dx |
|
|
= |
|
m2 − m1 |
gt |
||||||||||||
dt |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
m1 + m2 |
||||||||||||
|
|
|
dx |
= |
|
m2 − m1 |
gt dt |
||||||||||||
Z |
|
|
|
|
m1 + m2 |
||||||||||||||
|
|
|
Z |
m1 |
+ m2 |
||||||||||||||
|
|
|
dx |
= |
|
|
|
|
|
m2 |
− m1 |
gt dt |
|||||||
|
|
|
|
1 |
|
m2 − m1 |
|
||||||||||||
|
|
|
x = |
|
|
gt2 + C′ |
|||||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
2 m1 + m2 |
|||||||||||
|
x(t) = |
|
1 |
|
m2 − m1 |
gt2 |
|||||||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
2 m1 + m2 |
|||||||||||
(64)
(65)
(66)
