1.11.5. Регрессионные модели множественной корреляции
Корреляционная зависимость результативного признака от нескольких факторов называется множественной корреляцией.
Регрессионной моделью множественной корреляции называется уравнение
,
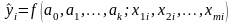где f – некоторая математическая функция;
– параметры;
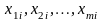– значения факторов
;
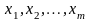– теоретические значения результативного признака.
Линейная модель корреляционной зависимости результативного признака y от m факторов имеет вид:
,
.
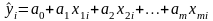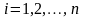(1.11.33)
Модель (1.11.33) так же, как и линейную модель (1.11.5) парной корреляции, можно записать в матричной форме (1.11.9), где
,
,
,
а МНК-оценки параметров этой модели можно вычислить по формуле (1.11.10).
Некоторые нелинейные регрессионные модели множественной корреляции сводятся к линейной модели. Рассмотрим некоторые из них.
1. Полулогарифмическая модель
,
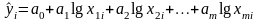(1.11.34)
является линейной
моделью относительно
.
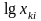2. Гиперболическая модель
,
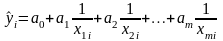(1.11.35)
является линейной
моделью относительно
.
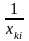3. Экспоненциальная модель
,
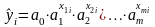(1.11.36)
логарифмированием преобразуется к линейной модели:
,.
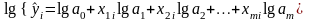(1.11.37)
4. Степенная модель
,
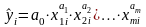(1.11.38)
логарифмированием преобразуется к линейной модели:
,.
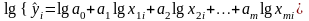(1.11.39)
Адекватность модели множественной корреляции оценивается средней ошибкой аппроксимации (1.11.19).
Коэффициент
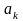линейной модели показывает, на сколько
единиц изменяется значение результативного
признака при увеличении k-го
фактора на
одну единицу.
Сравнение МНК-оценок параметров линейной модели дает представление о степени влияния факторов на результативный признак только тогда, когда они сопоставимы. Чтобы сделать эти оценки сопоставимыми, их нормируют по формуле
,
(1.11.40)
где
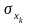и
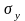
среднеквадратические отклонения
соответственно k-го
фактора и результативного признака.
Частный коэффициент эластичности:
,
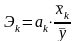(1.11.41)
где
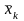
среднее значение k-го
фактора,
среднее значение результативного признака,
коэффициент линейной модели при k-ом факторе,
показывает, на сколько процентов в среднем изменяется результативный признак при изменении k-го фактора на 1%.
Сила связи линейной множественной корреляции оценивается с помощью коэффициента множественной корреляции, вычисляемого по формуле
.
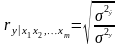(1.11.42)
Значение коэффициента множественной корреляции на значимость проверяется по правилу:
вычислить эмпирическое значение
,
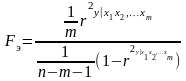(1.11.43)
где n – число наблюдений, m – число факторов;
2) найти
в табл. П5 по числам
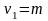и
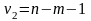и уровню значимости
критическое значение
;
3)
если
,
то
коэффициент множественной корреляции
признается значимым с вероятностью
.
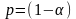В случае двухфакторной линейной корреляции множественный коэффициент корреляции можно вычислить, зная линейные коэффициенты парных корреляций, по формуле
.
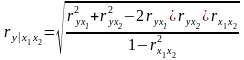(1. 11.44)
Для оценки вклада во множественный коэффициент корреляции каждого из факторов вычисляют частные коэффициенты корреляции, т. е. коэффициенты корреляции, в которой исключается влияние одного фактора. В случае двухфакторной линейной корреляции частные коэффициенты корреляции вычисляются по формулам
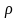и
.
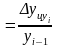(1.11.45)
Квадрат частного коэффициента корреляции называется частным коэффициентом детерминации. Он указывает вклад фактора в колеблемость результативного признака.
Наличие мультиколлинеарности, т. е. линейной зависимости меж-ду факторами, приводит к искажению значений параметров линейной модели и изменению смысла их экономической интерпретации. Эта проблема решается в эконометрике.
Пример
1.11.3. В
табл. 1.11.11 приведена зависимость прибыли
у
млн. руб.
от затрат
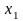коп.
на 1 руб. произведенной продукции
и от стоимости
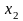млрд. руб. основных фондов предприятия.
Таблица 1.11.11
i |
|
|
|
i |
|
|
|
1 |
221 |
96 |
4,3 |
4 |
606 |
89 |
3,9 |
2 |
1070 |
77 |
5,9 |
5 |
779 |
82 |
4,3 |
3 |
1001 |
77 |
5,9 |
6 |
789 |
81 |
4,9 |
Составим линейную модель (1.11.9) данной зависимости, где
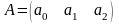и
.
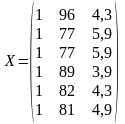Найдем МНК-оценки параметров модели по формуле (1.11.10), применяя функции МУМНОЖ и МОБР для вычисления в Excel произведения матриц и обратной матрицы:
=
=
,
,
=
,
=
=
.
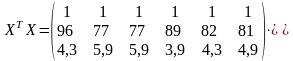
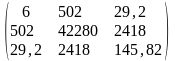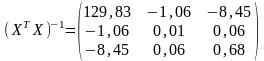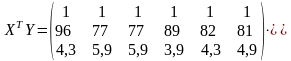
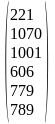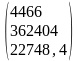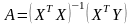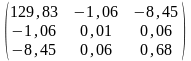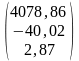Таким образом, линейная регрессионная модель зависимости прибыли от затрат на 1 руб. произведенной продукции и от стоимости основных фондов имеет вид:
.
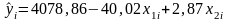(1.11.46)
Для вычисления средней ошибки аппроксимации (1.11.19) модели (1.11.46) и частных коэффициентов эластичности составим расчетную табл. 1.11.12. Вычислим:
средние значения:
,
,
;
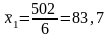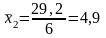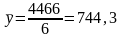среднюю ошибку аппроксимации:
;
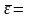
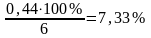частные коэффициенты эластичност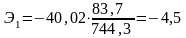и:
и
.
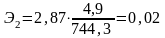Таблица 1.11.12