Расчетные показатели

7	95	–2	-14	28
10	105	-1	-10	10
15	115	0	0	0
12	125	1	12	12
			-12	50

Применяя формулы (1.8.4) и (1.9.6) и суммы в итоговой строке табл. 1.9.5, получим:

, .

Упражнение 1.9.3. Вычислите среднее значение и дисперсию по данным табл. 1.9.5, применяя формулы (1.8.4) и (1.9.6).

Дисперсию, среднее линейное отклонение и среднеквадратическое отклонение признака, значения которого несгруппированы, можно вычислить, применяя Excel, с помощью статистических функций ДИСПР, СРОТКЛОН и СТАНДОТКЛОНА. На рис. 1.9.2 изображен лист, на котором с помощью указанных функций вычислены показатели вариации распределения пар обуви по размерам (пример 1.5.1).

Упражнение 1.9.2. С помощью функций ДИСПР, СРОТКЛОН и СТАНДОТКЛОНА вычислите дисперсию, среднее линейное отклонение и среднеквадратическое отклонение признака по данным в упражнении 1.5.1.

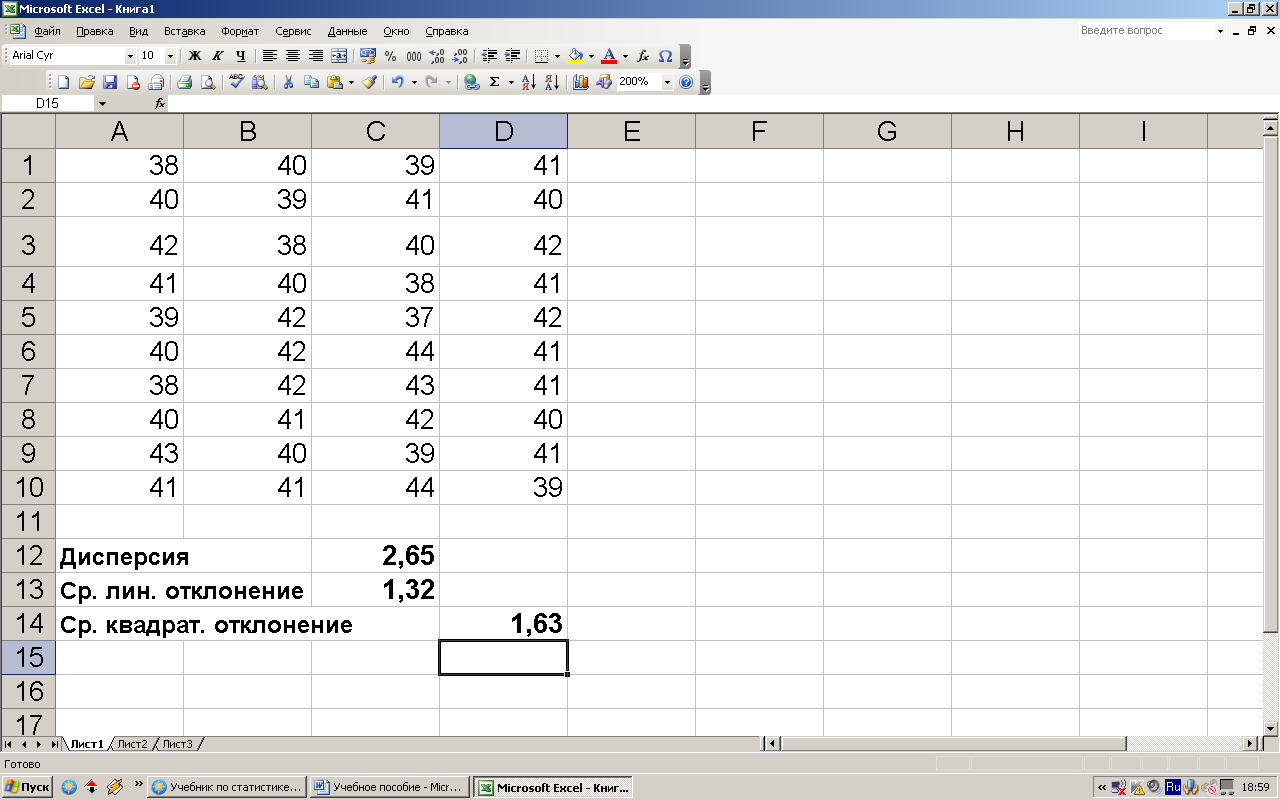
Рис. 1.9.2. Показатели вариации распределения пар обуви по размерам

1.9.2. Дисперсия альтернативного признака

Обозначая долю единиц совокупности, обладающих альтернативным признаком х, через р, а не обладающих – через q (p+q=1), вычислим дисперсию по формуле (1.9.5):

.

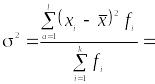
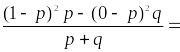
Таким образом, дисперсия альтернативного признака вычисляется по формуле:

. (1.9.7)

Пример 1.9.6. По данным примера 1.8.10 вычислим дисперсию и среднеквадратическое отклонение признака «изделие  нестандартное». Полагая в формуле (1.9.7) , получим:

, .

Упражнение 1.9.4. По данным, приведенным в упражнении 1.8.5, вычислите дисперсию и среднеквадратическое отклонение признака «студент получил неудовлетворительную оценку за контрольную работу по статистике».

1.9.3. Относительные показатели вариации

Относительные показатели вариации представляют собой отношения абсолютных показателей вариации к среднему значению, выраженные в процентах.

Коэффициент осцилляции:

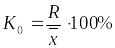(1.9.8)

характеризует колеблемость крайних значений признака около его среднего значения.

Относительное линейное отклонение:

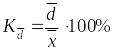(1.9.9)

характеризует долю усредненного значения абсолютных отклонений значений признака от его среднего значения.

Коэффициент вариации:

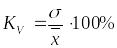(1.9.10)

характеризует однородность статистической совокупности по группировочному признаку: если , то статистическую совокупность можно считать однородной.

Упражнение 1.9.5. Вычислите относительные показатели вариации по данным, приведенным в табл. 1.9.5, и сформулируйте вывод об однородности предприятий по объему товарооборота.

1.9.4. Изучение влияния факторов на вариацию признака

Признак F, влияющий на признак х, называется фактором.

Пусть вариационный ряд распределения единиц статистической совокупности по группировочному признаку х разбит на k рядов по некоторому фактору F.

Дисперсия признака х характеризует его вариацию, обусловленную влиянием всех факторов, включая фактор F. Поэтому эта дисперсия называется общей дисперсией.

Часть вариации, которая обусловлена фактором F, характеризуется межгрупповой дисперсией, вычисляемой по формуле:

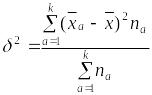, (1.9.11)

где – среднее значение признака х в а-й группе,

– численность единиц а-й группы.

Разность характеризует ту часть вариации признака х, которая возникает под влиянием всех факторов, кроме фактора F. Эта разность равна арифметическому среднему значению групповых дисперсий:

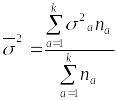, (1.9.12)

где – дисперсия признака х в а-й группе.

Равенство = называется правилом сложения дисперсий.

Доля дисперсии признака х, которая возникает под влиянием фактора F, вычисляется по формуле:

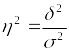. (1.9.13)

Число (1.9.13) называется эмпирическим коэффициентом детерминации. Арифметический квадратный корень из коэффициента (1.9.13):

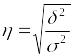(1.9.14)

называется эмпирическим корреляционным отношением

Отношение (1.9.14) оценивает влияние фактора F на вариацию признака х. Оно изменяется от 0 до 1. Если η = 0, то признак F не влияет на признак х и поэтому не является фактором. Если η = 1, то F – единственный фактор, влияющий на признак х. Чем ближе число η к 1, тем сильнее фактор F влияет на вариацию признака х.

Заметим, что в силу правила сложения дисперсий эмпирическое корреляционное отношение можно вычислять также по формуле

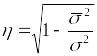. (1.9.15)

Пример 1.9.7. Интервальный ряд распределения магазинов по объему товарооборота (табл. 1.9.4) разбит на два ряда по числу работников (табл. 1.9.7). В первый ряд вошли магазины с числом работников, меньшим или равным 50 чел.

Оценим влияние количества работников на товарооборот магазинов. Среднее значение и дисперсия ряда, представленного табл. 1.9.4, были вычислены в примере 1.9.4 (рис. 1.9.1): млн. руб., . Применяя Excel, вычислим групповые дисперсии (рис. 1.9.3). Вычислим среднее значение групповых дисперсий:

и межгрупповую дисперсию:

.

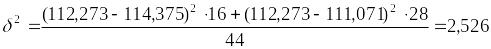Проверяем вычисления по правилу сложения дисперсий:

103,673+2,526=106,199.

Таблица 1.9.7