23. Решение одиночных нелинейных уравнений Решение одиночных нелинейных уравнений
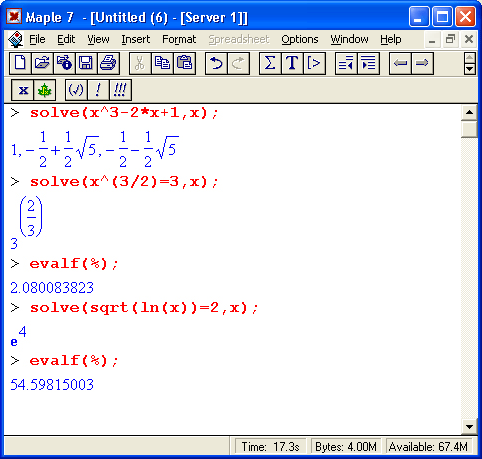
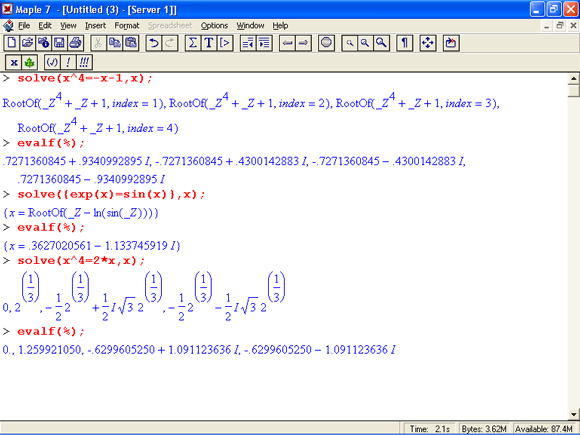
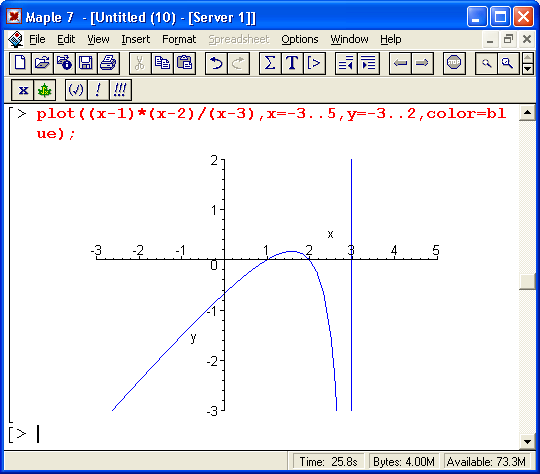
Решение одиночных нелинейных уравнений вида f(x) = 0 легко обеспечивается функций solve(f,(x),x). Это демонстрируют следующие примеры:
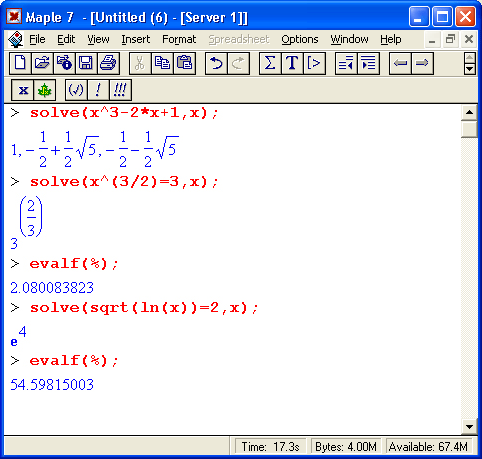
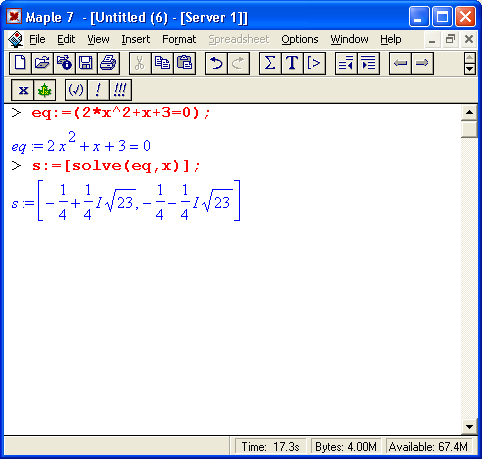
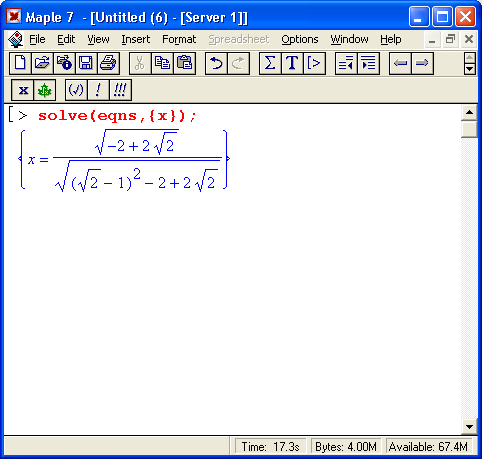
Часто бывает удобно представлять уравнение и его решение в виде отдельных объектов, отождествленных с определенной переменной:
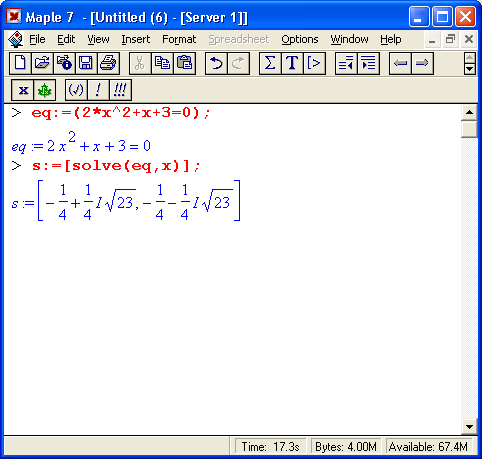
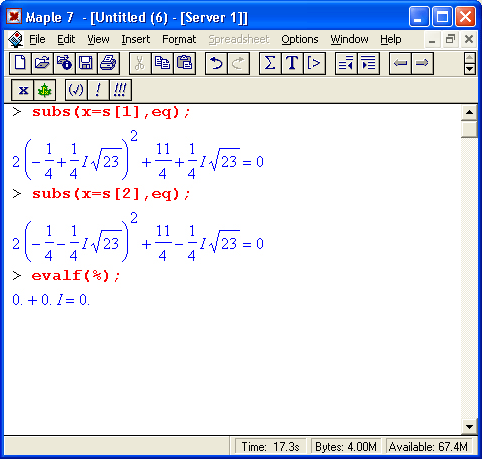
В частности, это позволяет легко проверить решение (даже если оно не одно, как в приведенном примере) подстановкой (subs):
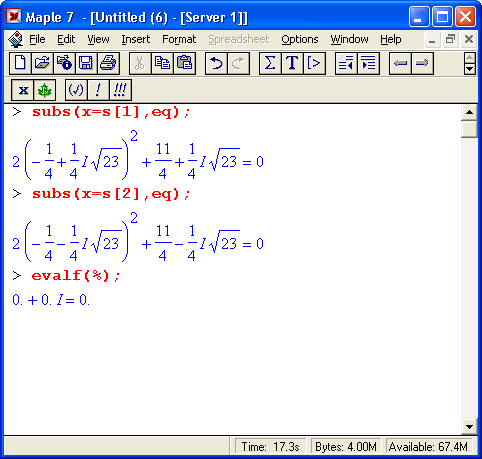
Сводящиеся к одному уравнению равенства вида f1(x)=fl(x) также решаются функцией solve(fl(x)=f2(x),x):
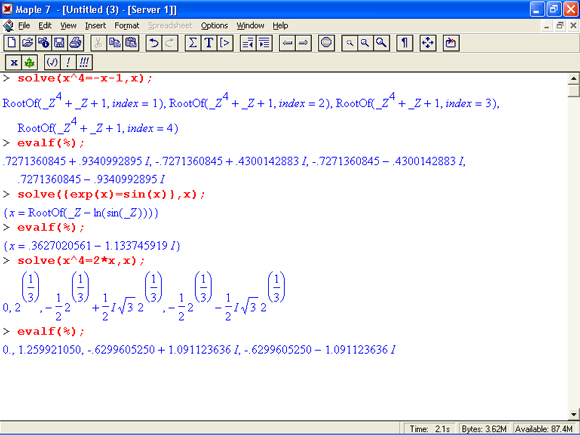
Обратите внимание в этих примерах на эффективность применения функции evalf, позволяющей получить решения, выраженные через функцию RootOf, в явном виде.
50.gif
51.gif
52.gif
53.gif
24. Решение тригонометрических уравнений
Решение тригонометрических уравнений
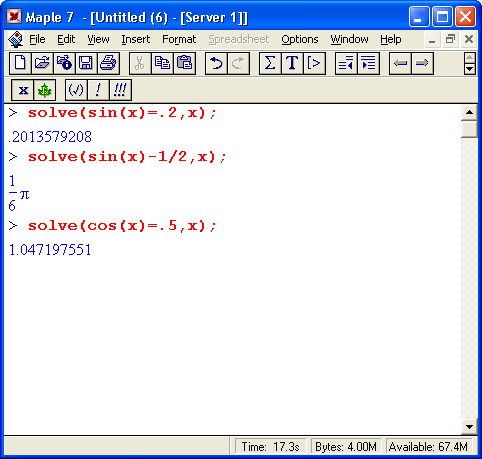
Функция solve может использоваться для решения тригонометрических уравнений:
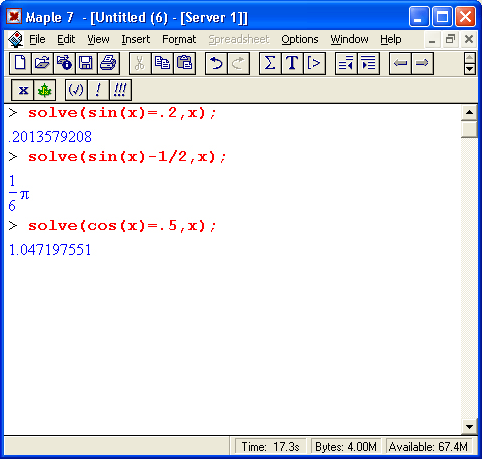
Однако из приведенных примеров видно, что при этом найдено только одно (главное) решение. Периодичность тригонометрических функций и связанная с этим множественность решений оказались проигнорированы. Однако можно попытаться найти все периодические решения, выполнив следующую команду:
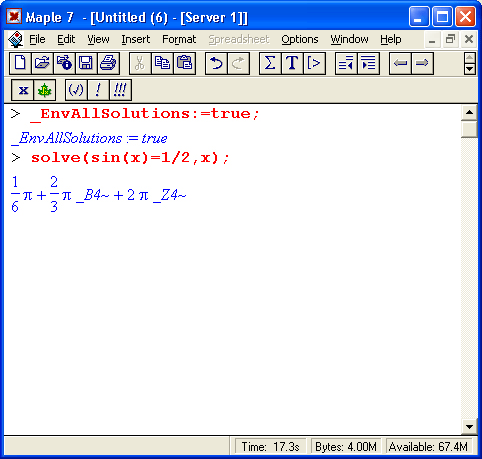
> _EnvAllSolutions:=true;
EnvAllSolutions := true
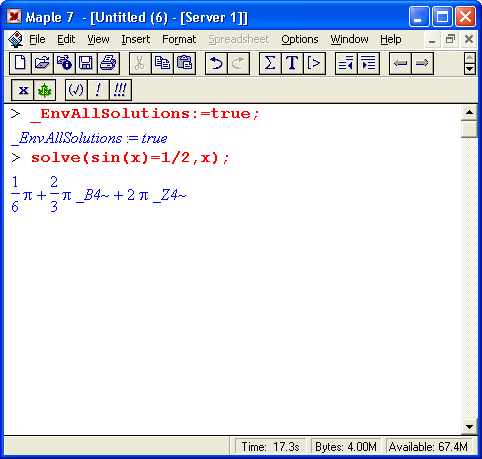
Указанная в ней системная переменная отвечает за поиск всех периодических решений, когда ее значение равно true, и дает поиск только главных решений при значении false, принятом по умолчанию. Так что теперь можно получить следующее:
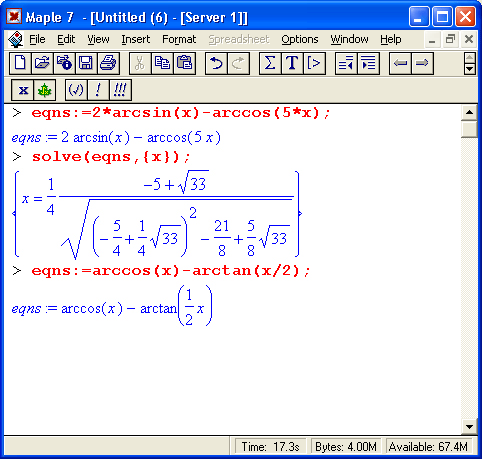
На рис. 8.11 показан более сложный случай решения нелинейного уравнения вида f1(x)=f2(x). где f1(х) = sin(x) и f2(x) = cos(x) - 1. Решение дано в графическом виде и в аналитическом для двух случаев — нахождения главных значений корней и нахождения всех корней.
В решениях встречаются переменные _В1- и _Z1~, означающие ряд натуральных чисел. Благодаря этому через них можно представить периодически повторяющиеся решения.
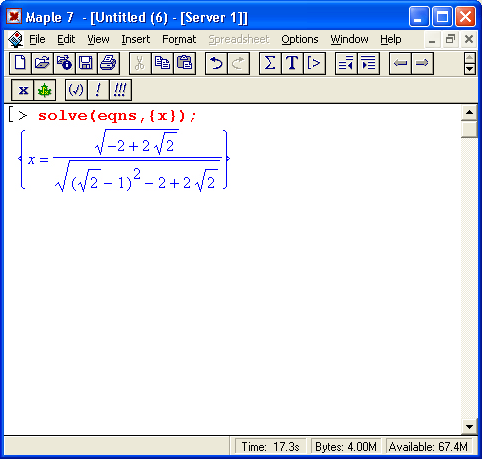
Примеры решения уравнений с обратными тригонометрическими функциями показаны ниже:
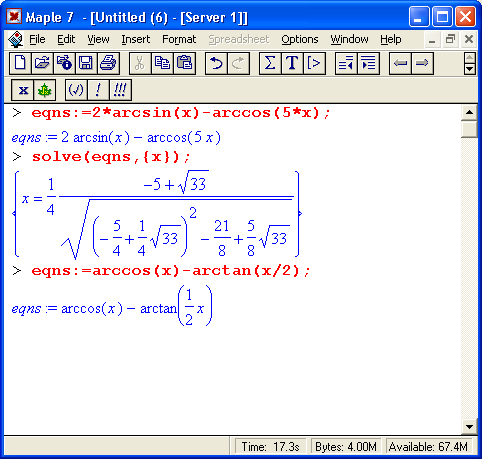
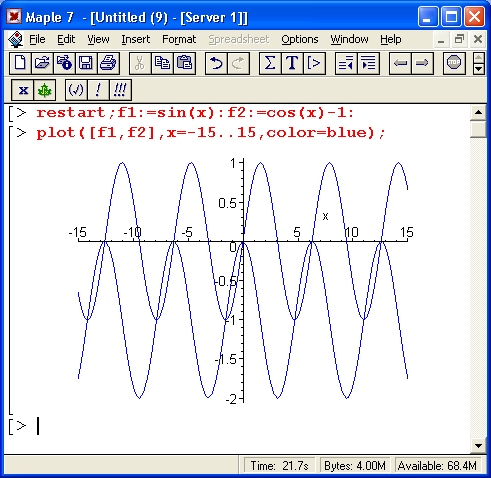
Рис. 8.11. Пример решения уравнения, имеющего периодические решения
54.gif
55.gif
56.gif
57.gif
67.gif
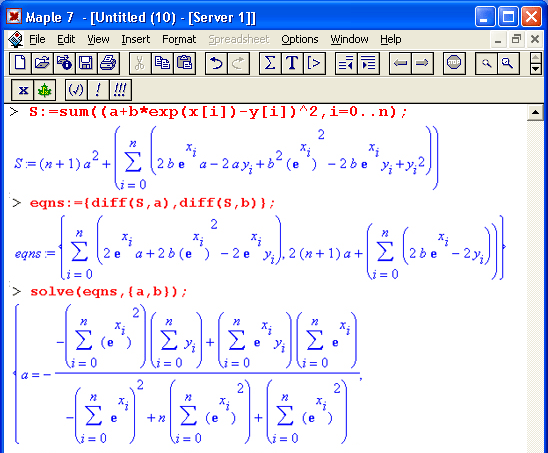
25. Решение систем линейных уравнений.
Решение систем линейных уравнений
Для решения систем линейных уравнений созданы мощные матричные методы, которые будут описаны отдельно. Однако функция solve также может с успехом решать системы линейных уравнений. Такое решение в силу простоты записи функции может быть предпочтительным. Для решения система уравнений и перечень неизвестных задаются в виде множеств (см. приведенные ниже примеры).
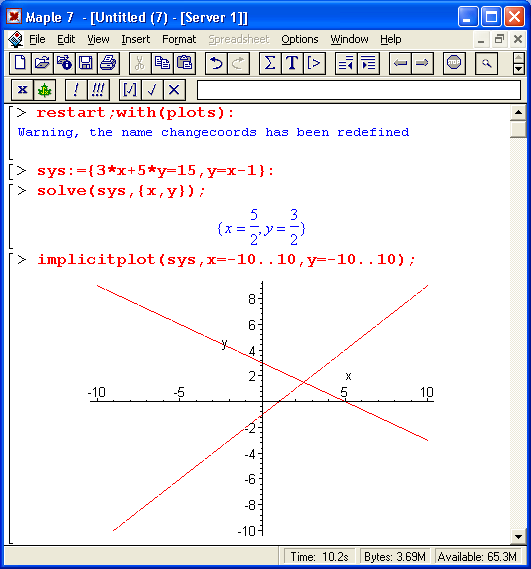
Рисунок 8.12 дает два примера решения систем из двух линейных уравнений. В первом примере функция solve возвращает решение в виде значений неизвестных х и у, а во втором отказывается это делать.
В чем дело? Оказывается, в том, что во втором случае система просто не имеет решения. Импликативная графика пакета расширения plots дает прекрасную возможность проиллюстрировать решение. Так, нетрудно заметить, что в первом случае геометрическая трактовка решения сводится к нахождению точки пересечения двух прямых, отображающих два уравнения. При этом имеется единственное решение, дающее значения х и у.
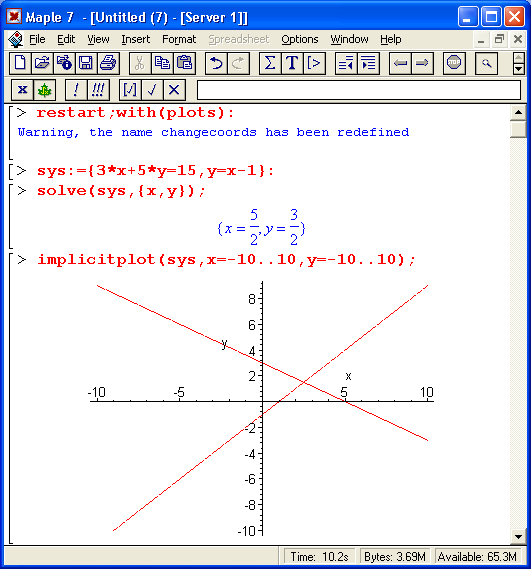
Рис. 8.12. Примеры решения системы из двух линейных уравнений с графической иллюстрацией
Во втором случае решения и впрямь нет, ибо уравнения задают параллельно расположенные прямые, которые никогда не пересекаются. Рекомендуем читателю самостоятельно проверить и третий случай — бесконечного множества решений. Он имеет место, если оба уравнения описывают одну и ту же зависимость и их графики сливаются в одну прямую.
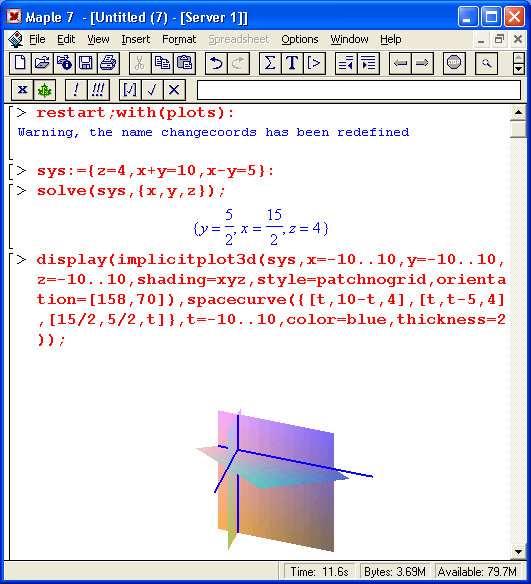
Решение систем из трех линейных уравнений также имеет наглядную геометрическую интерпретацию — в виде точки, в которой пересекаются три плоскости, каждая из которых описывается функцией двух переменных. Для наглядности желательно представить и линии пересечения плоскостей. Это позволяет сделать функция импликативной трехмерной графики tmplicitplotSd, что и показано на рис. 8.13. Для объединения графиков площадей использована функция display.
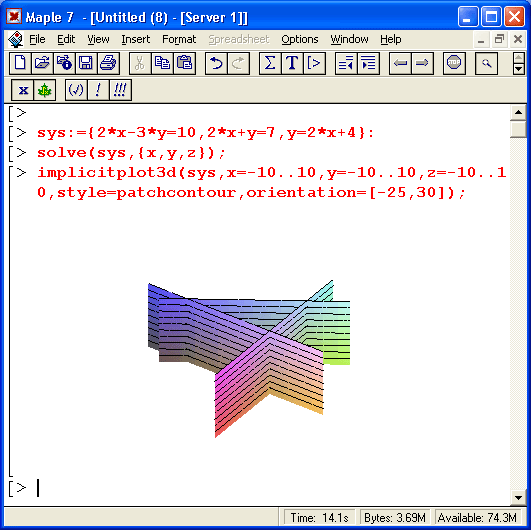
Некоторые проблемы с решением систем из трех линейных уравнений иллюстрируют примеры, приведенные на рис. 8.14, В первом примере решения вообще нет. График показывает, в чем дело, — линии пересечения плоскостей идут параллельно и нигде не пересекаются. Во втором примере все три плоскости пересекаются по одной линии.
Рис. 8.13.Пример решения системы из трех линейных уравнений с графической иллюстрацией решения
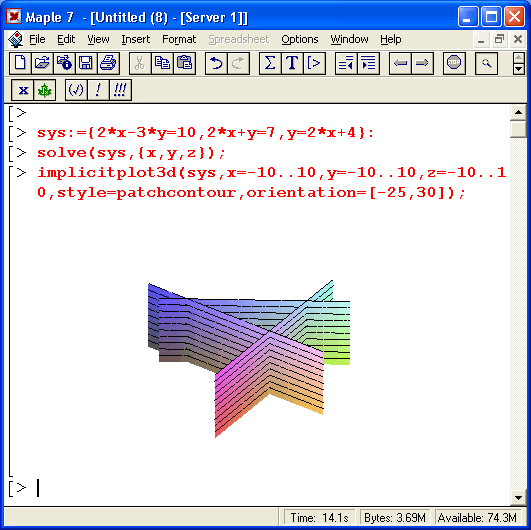
Рис. 8.14.Графическая иллюстрация особых случаев решения системы из трех линейных уравнений
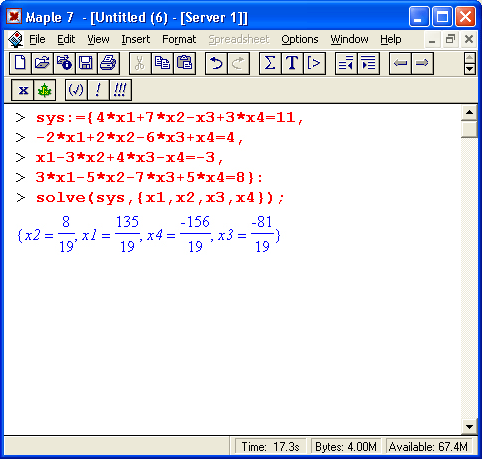
Следующий пример показывает решение системы из четырех линейных уравнений:
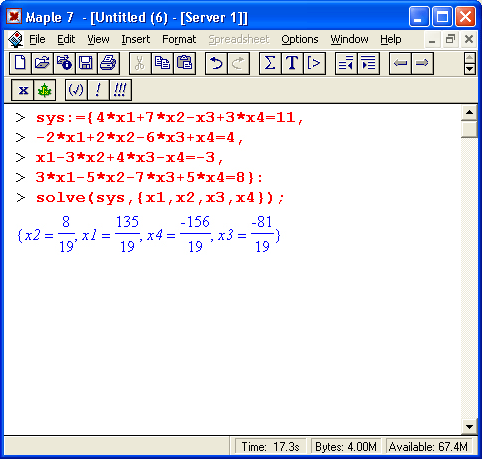
Эта система имеет решение, но его простая графическая иллюстрация уже невозможна.
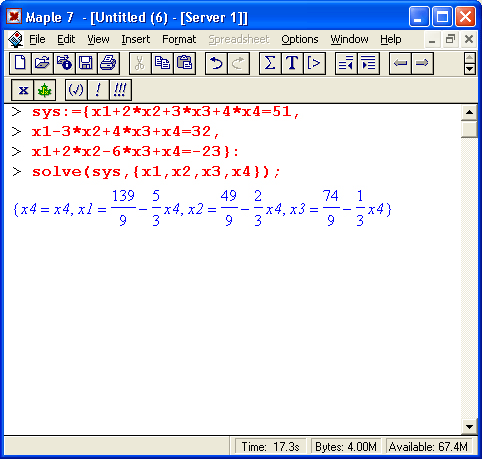
Случай решения неполной системы уравнений (уравнений — 3, а неизвестных — 4) иллюстрирует следующий пример:
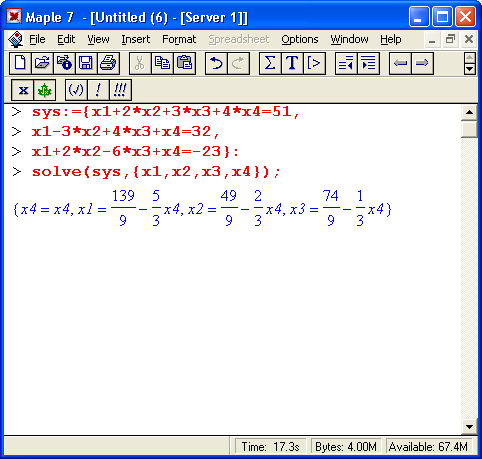
Как видно из приведенных примеров, функция solve неплохо справляется с решением систем линейных уравнений.
58.gif
59.gif
83.gif
84.gif
85.gif
26. Решение систем нелинейных и трансцендентных уравнений
Решение систем нелинейных и трансцендентных уравнений
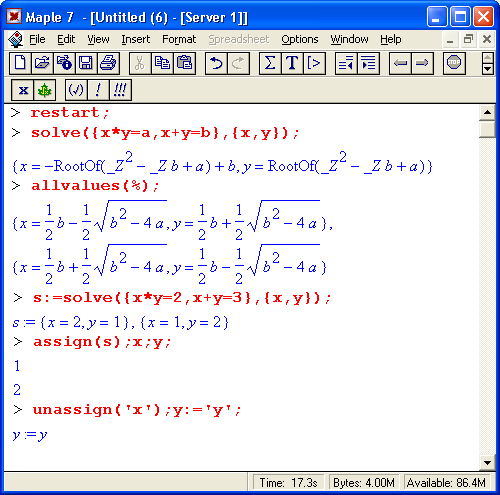
Функция solve может использоваться для решения систем нелинейных и трансцендентных уравнений. Для этого система уравнений и перечень неизвестных задаются в виде множеств. Ниже приведены примеры решения уравнений:
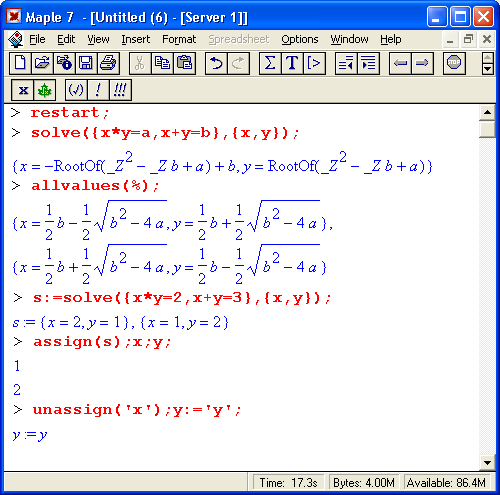
В этих примерах хорошо видна техника работы с функциями solve и assign. В конце примеров показано восстановление неопределенного статуса переменных х и у с помощью функции unassign и снятие определения переменных с помощью заключения их в прямые апострофы.
60.gif
27. Функция RootOf.
Функция RootOf
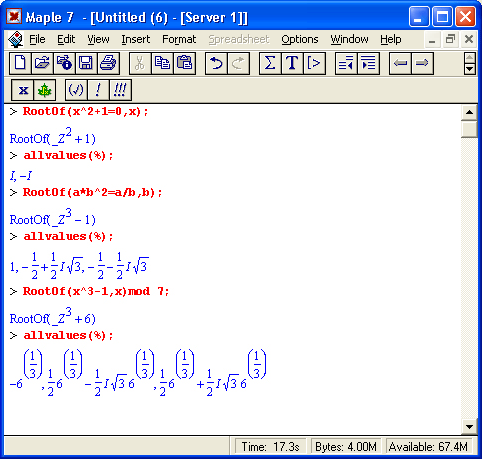
В решениях уравнений нередко появляется функция RootOf, означающая, что корни нельзя выразить в радикалах. Эта функция применяется и самостоятельно в виде RootOf(ехрr) или RootOf(ехрr, х), где ехрr — алгебраическое выражение или равенство, х — имя переменной, относительно которой ищется решение. Если х не указана, ищется универсальное решение по переменной _Z. Когда ехрr задано не в виде равенства, решается уравнение ехрr=0. Для получения решений вида RootOf в явном виде может использоваться функция all values. Примеры применения функции RootOf:
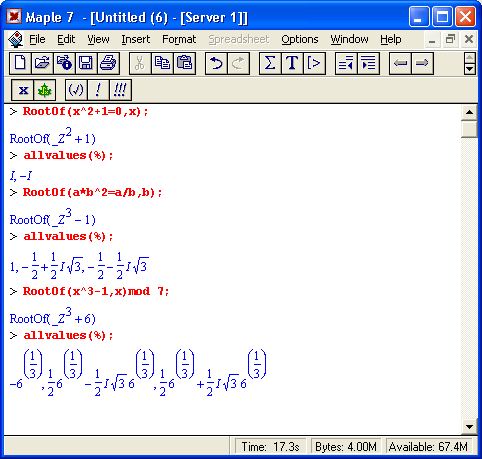
Итак, функция RootOf является эффективным способом представления решения в компактном виде. Как уже отмечалось, наряду с самостоятельным применением она часто встречается в составе результатов решения нелинейных уравнений.
61.gif
28. Решение уравнений со специальными функциями
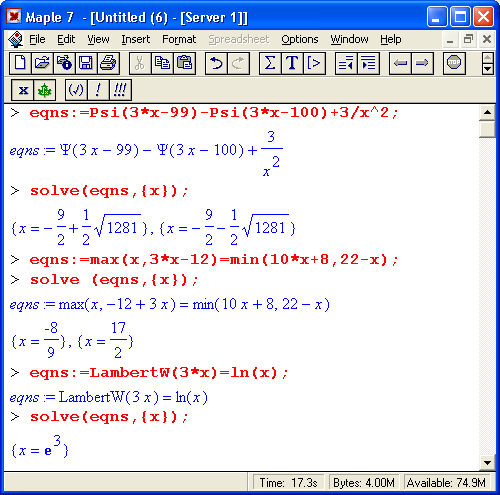
Решение уравнений со специальными функциями
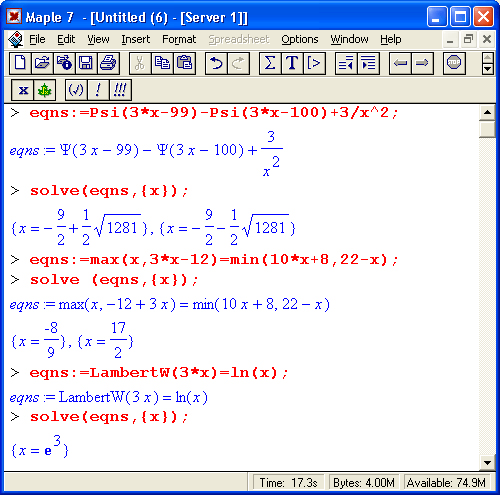
К важным достоинствам Maple 7 относится возможность решения уравнений, содержащих специальные функции как в записи исходных выражений, так и в результатах решения. Приведем несколько примеров такого рода:
62.gif
29. Решение неравенств
Решение неравенств
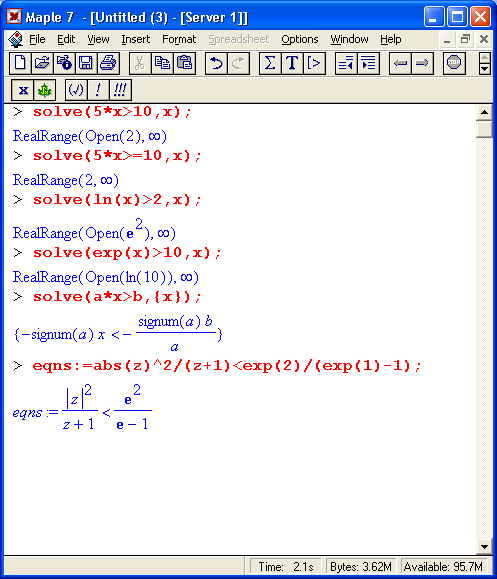
Неравенства в математике встречаются почти столь же часто, как и равенства. Они вводятся знаками отношений, например: > (больше), < (меньше) и т. д. Решение неравенств существенно расширяет возможности функции solve. При этом неравенства задаются так же, как и равенства. Приведенные на рис. 8.15 примеры поясняют технику решения неравенств.
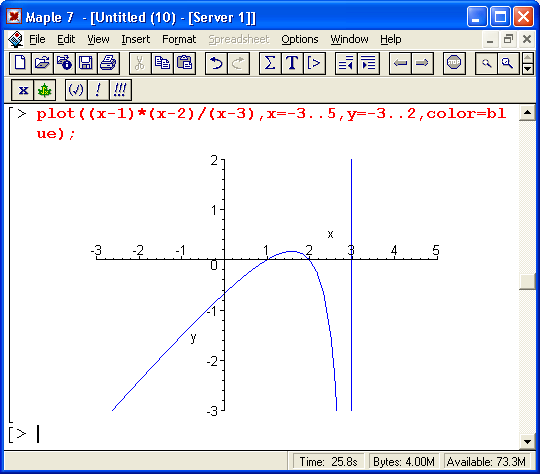
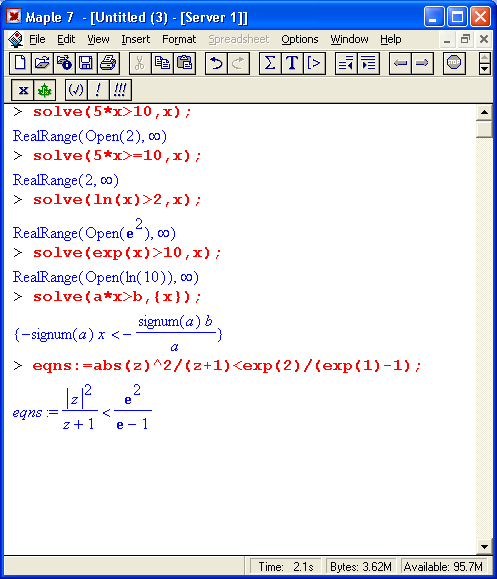
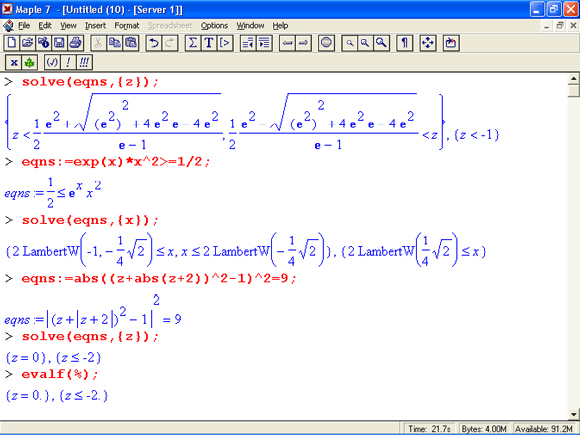
Из приведенных примеров очевидна форма решений — представлены критические значения аргумента, вплоть до не включаемых значений области действия неравенства (они указываются словом Open). Всегда разумным является построение графика выражения, которое задает неравенство, — это позволяет наглядно убедиться в правильности решения. Приведем еще несколько примеров решения неравенств в аналитической форме:
а
б
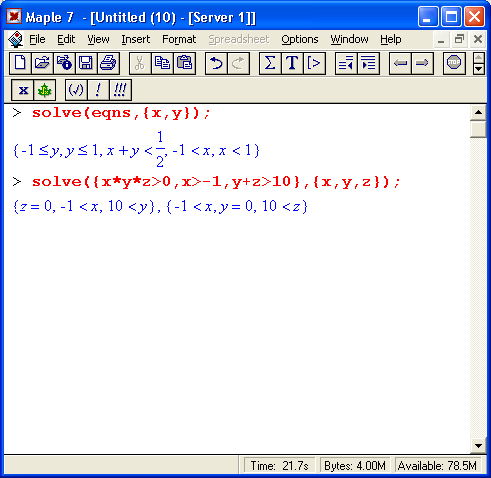
Рис. 8.15. Примеры, иллюстрирующие решение неравенств
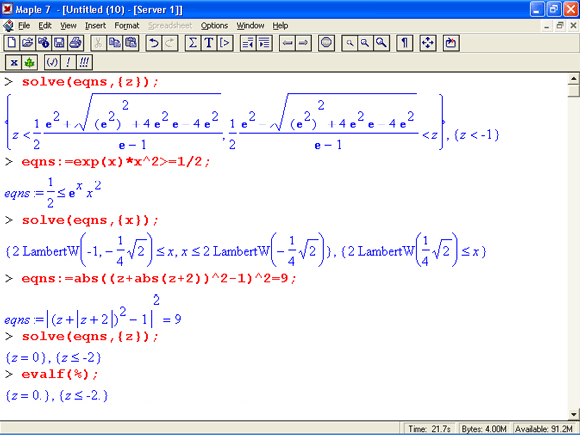
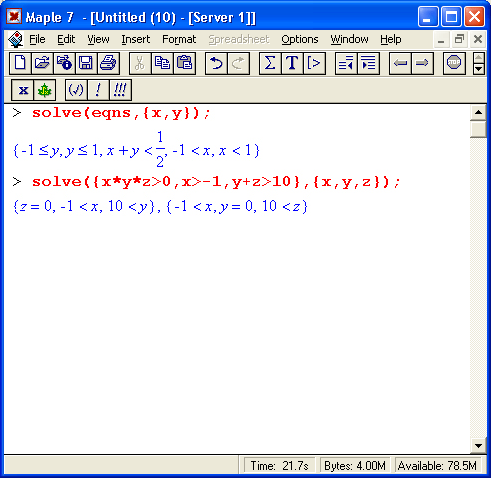
В последних примерах показано решение систем неравенств." При этом выдаются области определения нескольких переменных.
63.gif
68.gif
69.gif
77.gif
30. Решение функциональных уравнений
Решение функциональных уравнений
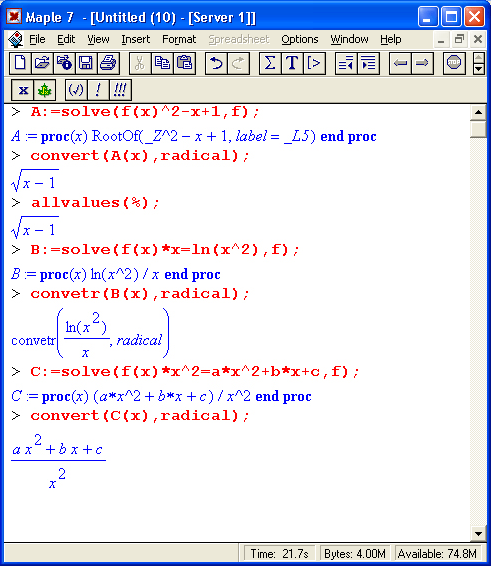
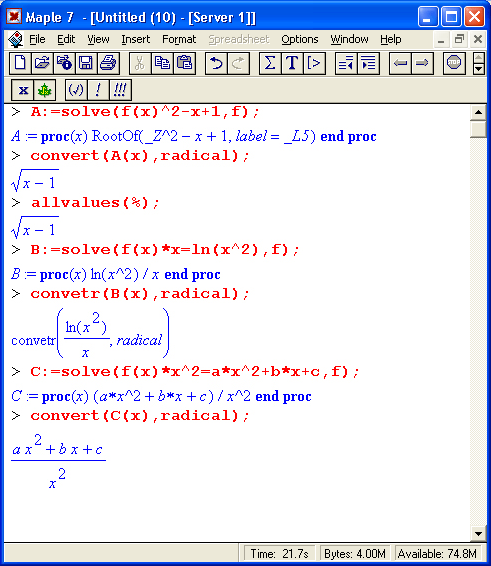
Решение функционального уравнения, содержащего в составе равенства некоторую функцию f(x), заключается в нахождении этой функции. Для этого можно использовать функцию solve, что демонстрируют приведенные ниже примеры:
70.gif
31. Решение уравнений с линейными операторами
Решение уравнений с линейными операторами
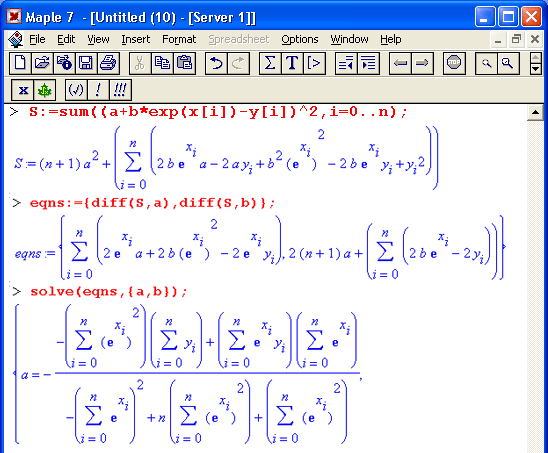
Maple 7 позволяет решать уравнения с линейными операторами, например с операторами суммирования рядов и дифференцирования. Ограничимся одним примером такого рода:
71.gif
32. Решение в численном виде — функция fsolve
Решение в численном виде — функция fsolve
Для получения численного решения нелинейного уравнения или системы нелинейных уравнений в форме вещественных чисел удобно использовать функцию:
fsolve( eqns. vars. options )
Эта функция может быть использована со следующими параметрами:
complex — находит один или все корни полинома в комплексной форме;
full digits — задает вычисления для полного числа цифр, заданного функцией Digits;
maxsols=n — задает нахождение только n корней;
interval — задается в виде а. .b или х=а. .b, или (х=а. .b, y=c. .d, ...} и обеспечивает поиск корней в указанном интервале.
Функция fsolve дает решения сразу в форме вещественных или комплексных чисел, что и показывают следующие примеры:
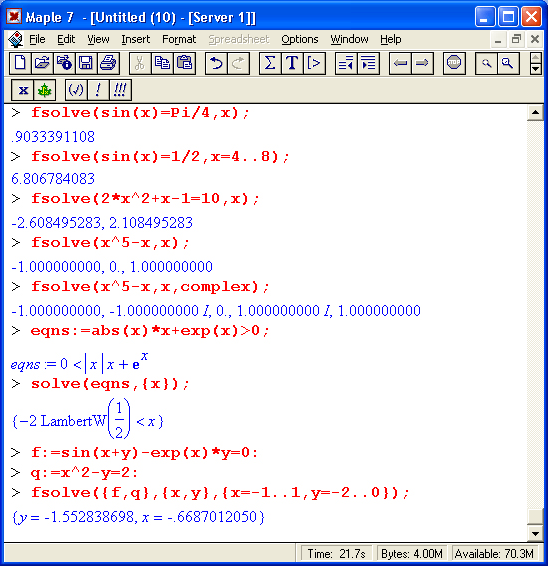
Заметим, что локализация поиска корней в заданном интервале позволяет отыскивать такие решения, которые не удается получить с помощью функций solve и fsolve в обычном применении. В последнем из приведенных примеров дается решение системы нелинейных уравнений, представленных уравнениями f и д.
Чтобы еще раз показать различие между функциями solve и fsolve, рассмотрим пример решения с их помощью одного и того же уравнения erf(x) = 1/2:
> so1ve(erf(x)=l/2,x);
RootOf(2erf(_Z)-l)
> fsolve(erf(x)=l/2);
.4769362762
Функция solve в этом случае находит нетривиальное решение в комплексной форме через функцию RootOf, тогда как функция fsolve находит обычное приближенное решение.
72.gif
