15. Моделирование и расчет электронных схем

Моделирование и расчет электронных схем

Нужно ли применять Maple для моделирования и расчета электронных схем?

Нужно ли применять системы компьютерной математики для анализа, расчета и моделирования электронных схем? Ответ на этот вопрос не так прост, как кажется с первого взгляда. С одной стороны, к услугам пользователя компьютера сейчас имеется ряд программ схемотехнического моделирования, например Micro-CAP, Electronics Workbench, PSpice, Design Labs и др., автоматически составляющих и решающих большие системы уравнений состояния электронных схем и моделирующих работу бесчисленного множества электронных схем без кропотливого «ручного» составления уравнений.

Но, с другой стороны, анализ схем в таких программах настолько автоматизирован, что начисто теряется его физическая и математическая сущность. Это не так уж страшно, когда моделируются типовые схемы на давно известных или, скорее, просто хорошо знакомых электронных приборах. Но это явно плохо, когда объектом исследования и моделирования являются новые нетрадиционные схемы на новых или малоизвестных приборах или когда знание физических и математических основ работы таких схем принципиально необходимо. Например, при изучении их в вузах и университетах. В этом случае применение систем компьютерной математики не только возможно, но и принципиально необходимо.

16. Малосигнальный анализ усилителя на полевом транзисторе

Малосигнальный анализ усилителя на полевом транзисторе

Рассмотрим классический усилительный каскад на полевом транзисторе, схема которого приведена на рис. 17.12, а. Его эквивалентная малосигнальная схема представлена на рис. 17.12, б.

a

б

Рис. 17.12. Принципиальная (о) и эквивалентная(6) схемы усилителя на полевом транзисторе

Наша цель заключается в расчете характеристик усилителя операторным методом. Подключим нужный нам пакет plots:

> restart:with(plots):

Warning, the name changecoords has been redefined

Из законов Киргофа вытекает, что сумма токов, втекающих в каждый узел и вытекающих из него равна 0. Следовательно, для узлов эквивалентной схемы рис. 17.12 можно записать следующую систему уравнений в операторной форме:

Переменные напряжения на узлах схемы находятся из аналитического решения данной системы. При этом заблокируем вывод их аналитических значений, поскольку он очень громоздок. Тем не менее вы можете посмотреть на полученные формулы, поставив знак точки с запятой вместо знака двоеточия в приведенных ниже выражениях:

> solve({eql,eq2,eq3.eq4}б{Vl,V2.V3,Vo}):

Обеспечим присвоение переменным Vo, VI, V2 и V3 найденных из решения системы уравнений значений:

> assign(%):

Теперь найдем операторную передаточную функцию в аналитическом виде:

В соответствии с выбранным операторным методом анализа введем обозначения:

Это позволяет найти Н как функцию от частоты f также в аналитическом виде:

Это тоже довольно громоздкое выражение, и его применение при «ручном» анализе потребовало бы от нас немало изобретательности. Между тем Maple 7 позволяет «в два счета» определить из него амплитудно-частотную (AVM) и фазо- частотную (PhaseAV) характеристики усилителя как функции частоты:

> AVM=-evalc(abs(H)):

> PhaseAV:=evalc(argument(H)):

Преобразуем AVD в логарифмическую характеристику, выражающую усиление в децибелах (dB):

> AVdB:=20*1og10(AVM):

Такая характеристика более привычна для специалистов в радиоэлектронике. Соответственно фазо-частотную характеристику выразим в градусах:

> R2D:=evalf(360/(2*Pi));R2D := 57.29577950

> AVdeg:=R2D*PhaseAV:

Теперь можно перейти к обычным численным расчетам. Зададим конкретные значения компонент эквивалентной схемы усилителя:

> Rl:=100: R2:=100000: R3:=1000: R4:=10000: Cl:=1.*10^(-6): С2:=5*10^(-12): СЗ:=1*10^(-6): mu:=50:

Построим амплитудно-частотную характеристику усилителя:

> gaindata:-NULL:

phasedata:=NULL:

for a from 0 to 8 do:

for i from 2*10^a to l(T(a+l) by 10^a do

gaindata:=gaindata, [1. evalf(subs(f=i,AVdB))];

phasedata:=phasedata, [i, eva1f(subs(f=i,AVdeg))]:

od: od:

> 1oglogp1ot([gaindata]. thickness»2, color=black, style=1ine, axes=boxed,

title=`Коэффициент усиления K(f)`,1abels=['Частота (Hz)VK(d8)']):

Она показана на рис. 17.13.

Рис. 17.13. Амплитудно-частотная характеристика усилителя

Далее зададим построение фазо-частотной характеристики усилителя:

> 1og1ogplot([phasedata], thickness=2, color=b1ue, style=line, axes=boxed, title='Фаэовый сдвиг (в градусах)`, labels=['Частота (Hz)','Фаза']);

Она представлена на рис. 17.14.

Рис. 17.14.Фазо-частотная характеристика усилителя

Найдем номинальный коэффициент усиления на частоте f=1000 (Гц):

> AVmid:=eva1f(subs(f=1000, AVdB)):

AVmid=33.12074854

Имея аналитическое выражение для амплитудно-частотной характеристики, можно составить уравнения для вычисления граничных частот (по спаду усиления на -dAV в dB):

> dAV:=3: #Ослабление (в dB на граничных частотах)

> eq5:=AVmid-dAV=20*log10(AVM):

Теперь можно найти эти частоты — нижнюю и верхнюю:

> flow:=fsolve(eq5,f. f-10..2000):flow:= 23.61659476

> fhigh:=fsolve(eqS,f, f-2000..100*10*6);

fliigh := .5737800225 107

Мы можем построить и более наглядную амплитудно-частотную характеристику с точками, соответствующими граничным частотам:

> with(plottools) :h:=log10(AVnvid-dAV):

aplot:= Loglogplot([gaindata], thickness=2, color=b1ack. style=line, axes=boxed,

title='Частоты flow и fhigh среза', labels=['Частота (Hz)VK(dB)']):

bplot:=line([0.1,h], [7.1,h], color=black, linestyle=3):

cplot:=line([log10(flow),0.58],[logHK flow). 1.6], color=blue, linestyle=3):

dplot:=line([log10(fh1gh).0.58],. [log10(fhigh).1.6],. color=red,. 1inestyle=3):

display([aplot.bplot,cplotJ,dplot]):

Эта характеристика показана на рис. 17.15.

На ней проставлены синяя и красная пунктирные вертикали, соответствующие найденным граничным частотам flow и fhigh, а также пунктирная горизонталь, соответствующая коэффициенту усиления на этих частотах. Это позволяет наглядно оценить частотный диапазон работы усилителя.

Таким образом, задача расчета усилителя в малосигнальном режиме полностью решена. Мы получили значение номинального коэффициента усиления, рассчитали нижнюю и верхнюю граничные частоты, получили аналитические выражения для амплитудно-частотной и фазо-частотной характеристик усилителя и построили их наглядные графики.

Рис. 17.15.Амплитудно-частотная характеристика с выделенными точками граничных частот

34.gif

36.gif

37.gif

38.gif

39.gif

40.gif

41.gif

42.gif

17. Расчет аналогового фильтра на операционном усилителе

Расчет аналогового фильтра на операционном усилителе

Теперь рассмотрим проектирование аналогового полосового фильтра на операционном усилителе, схема которого приведена на рис. 17.16.

Рис. 17.16.Схема полосового фильтра на интегральном операционном усилителе

Подготовимся к расчету фильтра:

> restart:

Зададим основные уравнения, описывающие работу фильтра на малом сигнале:

Введем круговую частоту:

> omega := 2*Pi*f;

W := 2пf

Найдем коэффициент передачи фильтра и его фазо-частотную характеристику как функции от частоты:

> gain := abs(eva1c(Vo/Vi)):

> phase := evalc(op(2,convert(Vo/Vi.polar))):

Для просмотра громоздких аналитических выражений для этих параметров замените знаки двоеточия у выражений для gain и phase на знак точки с запятой. Далее введем конкретные исходные данные для расчета:

> R3 :=1000:

> R4 := 3000:

> СЗ :=0.08*10^(-6):

> С4 := 0.01*10^(-6):

Построим АЧХ фильтра как зависимость коэффициента передачи в децибелах (dB) от частоты f в Гц:

> plot(DogWf), 20*log10(gain), f=[10..50000], color=black, title='Коэффициент передачи dB как функция от частоты f в Гц'):

Эта характеристика представлена на рис. 17.17. Здесь полезно обратить внимание на то, что спад усиления на низких и высоких частотах происходит довольно медленно из-за малого порядка фильтра.

Рис. 17.17. АЧХ фильтра на операционной усилителе

Далее построим фазо-частотную характеристику фильтра как зависимость фазы в радианах от частоты f в Гц:

> plot ([log10(f),phase, f=10..50000], color=black, title=*Фазо-частотная характеристика фильтра*);

Фазо-частотная характеристика (ФЧХ) фильтра показана на рис. 17.18

На ФЧХ фильтра можно заметить характерный разрыв, связанный с превышением фазовым углом граничного значения я. Такой способ представления фазового сдвига общепринят, поскольку его изменения стремятся вписать в диапазон от -я до п.

Рис. 17.18.ФЧХ фильтра на операционном усилителе

43.gif

44.gif

45.gif

46.gif

18. Проектирование цифрового фильтра

Проектирование цифрового фильтра

Основной недостаток аналоговых активных фильтров, подобных описанному выше, заключается в их малом порядке. Его повышение за счет применения многих звеньев низкого порядка ведет к значительному повышению габаритов фильтров и их стоимости. От этого недостатка свободны современные цифровые фильтры, число ячеек которых N даже при однокристальном исполнении может достигать десятков и сотен. Это обеспечивает повышенную частотную селекцию.

Спроектируем фильтр N+1-ro порядка класса FIR (Finite Impulse Response или с конечной импульсной характеристикой). Каждая из N ячеек временной задержки фильтра удовлетворяет следующей зависимости выходного сигнала у от входного х вида:

Подключим пакет расширения plots, нужный для графической визуализации проектирования:

> restart:with(p1ots):

Warning, the name changecoords has been redefined

Зададим исходные данные для проектирования полосового цифрового фильтра, выделяющего пятую гармонику из входного сигнала в виде зашумленного меандра с частотой 500 Гц:

> N := 64: # Число секций фильтра (на 1 меньше порядка фильтра)

> fs:= 10000: # Частота квантования

> fl = 2300: # Нижняя граничная частота

> fh = 2700: # Верхняя граничная частота

> m := 10: # 2^m > N - число точек для анализа

Вычислим:

Вычислим FIR-коэффициенты для прямоугольного окна фильтра:

> С :-=(n) -> limit(g,t=n):h := aray(0..N): N2:=N/2:

> for n from 0 to N2 do h[N2-n]:= evalf(C(n)); h[N2+n] := h[N2-n]; od:

Определим массивы входного x(n) и выходного у(n) сигналов:

> х := array(-N..T): y := аггау(0..Т):

Установим значение х(n) равным 0 для времени меньше 0 и 1 для времени >=0:

> for n from -N to -1 do x[n] := 0; od:

> for n from 0 to Т do x[n] := Dirac(n); od:

Вычислим временную зависимость для выходного сигнала:

> for n from 0 to Т do y[n] := sum(h[k]*x[n-k],k=0..N): od:

Построим график импульсной характеристики фильтра, отражающей его реакцию на сигнал единичной площади с бесконечно малым временем действия:

> р := [seq([j/fs,y[j]],j=0..T)3:

> plot(p, time=0..3*N/fs, labels=[time,output], axes=boxed, xtickmarks=4, title-'Иипульсная характеристика фильтра',color=black);

Он показан на рис. 17.19. Нетрудно заметить, что эта характеристика свидетельствует об узкополосности фильтра, поскольку его частоты fl и fh различаются несильно. В этом случае полосовой фильтр по своим свойствам приближается к резонансному, хотя само по себе явление резонанса не используется.

Рис. 17.19.Импульсная характеристика цифрового фильтра

Вычислим АЧХ фильтра, используя прямое преобразование Фурье. Оно после подготовки обрабатываемых массивов реализуется функцией FFT:

> rо := array (1..T+1): io := arrayd. .T+l):

> for n from 0 to Т do ro[n+l] :- y[n]; io[n+l] := 0; od:

> FFT(m,ro,io):

Построим график АЧХ фильтра:

> р :=[seq([j*fs/(T+l),abs(ro[j+l]+io[j+l]*I)3,j=O..T/2)]:

> plot(p, frequency=0..fs/2, tabels=[frequency,gain], tit1e='AЧX фильтра',со1ог=black);

Он представлен на рис. 17.20. Нетрудно заметить, что и впрямь АЧХ фильтра напоминает АЧХ резонансной цепи — она имеет вид узкого пика. Вы можете легко проверить, что раздвижением частот fl и fh можно получить АЧХ с довольно плоской вершиной и резкими спадами (говорят, что такая характеристика приближается к прямоугольной).

Рис. 17.20. АЧХ цифрового полосового фильтра

Теперь приступим к тестированию фильтра. Зададим входной сигнал в виде зашумленного меандра с частотой 500 Гц и размахом напряжения 2 В:

> 1 :=round(fs/2/500):

> for n from 0 by 2*1 to Т do

> for n2 from 0 to 1-1 do

> if n+n2 <= Т then

> x[n+n2] := evalf(-l+rand()/10^12-0.5);

> fi:

> if n+n2+1 <= Т then

> x[n+n2-H] :-=eva1f(l+ranoX)/10^12-0.5);

> fi;

> od:

> od:

Временная зависимость синтезированного входного сигнала представлена на рис. 17.21.

Рис. 17.21. Синтезированный входной сигнал

Вычислим реакцию фильтра на входной сигнал:

> for n from 0 to T do

> y[n] := sum(h[k]*x[n-k],k=0..N);

> od:

Построим график выходного сигнала:

> р := [seq([j/fs, x[j]], j=0..T)]:q:= [seq([j/fs , y[j]] , j =0..Т)]:

> plot(p,time=0..T/fs/4,1abels=[time,volts],title='Входной сигнал\сolor=black);

> plot(q,tine=0..T/fs/4,1abels=[tirae,volts], titlе='Выходной сигнал",color=black);

Временная зависимость выходного сигнала показана на рис. 17.22. Нетрудно заметить, что в конце концов выходной сигнал вырождается в пятую гармонику входного сигнала, но этому предшествует довольно заметный переходной процесс. Он связан с узкополосностью данного фильтра.

Рис. 17.22.Временная зависимость выходного сигнала цифрового фильтра

Вычислим спектры входного и выходного сигналов, подготовив массивы выборок сигналов и применив прямое преобразование Фурье с помощью функции FFT:

> Н := array(l..T+l):1i :=array(1..Т+1):

> for n from 0 to T do ,

> ri[n+l] := x[n]*2/T: ii[rn-l] := 0;

> ro[n+l] := y[n]*2/T; Io[rrfl] := 0;

> od:

> FFT(m.ri,ii):rTT(m,ro,io):

Построим график спектра входного сигнала, ограничив масштаб по амплитуде значением 0,5 В:

> р := [seq([j*fs/(T+l),abs(n[j+l]+ii[j-H]*I)],j=0..T/2)]:

> q := [seq([j*fs/(T-H),abs(ro[j-H]+To[j+l]*I)],j=0..T/2)]:

> plot(p, frequency=0..fs/2,y0..0.5,labe1s=[Частотa.V],title='Частотный спектр входного сигнала',color=black);

Этот график представлен на рис. 17.23. Из него хорошо видно, что спектральный состав входного сигнала представлен только нечетными гармониками, амплитуда которых убывает по мере роста номера гармоники. Пятая гармоника на частоте 2500 Гц находится посередине полосы пропускания фильтра, ограниченной граничными частотами фильтра 2300 и 2700 Гц. Заметны также беспорядочные спектральные линии шума сигнала в пределах полосы прозрачности фильтра.

Теперь построим график спектра выходного сигнала:

> p1ot(q, frequency=0..fs/2,y=0..0.5,labe1s=[Частотa,V], title='Частотный спектр выходного сигнала'бcolor=black);

Он представлен на рис.17.24. Хорошо видно эффективное выделение пятой гармоники сигнала и прилегающей к ней узкой полосы шумового спектра.

Рис. 17.23.Спектрограмма входного сигнала

Рис. 17.24. Спектрограмма выходного сигнала цифрового фильтра

Приведенные данные свидетельствуют, что спроектированный фильтр полностью отвечает заданным требованиям и обеспечивает уверенное выделение пятой гармоники зашумленного меандра. По образу и подобию данного документа можно выполнить проектирование и других видов цифровых фильтров.

47.gif

48.gif

49.gif

50.gif

51.gif

52.gif

53.gif

54.gif

19. Моделирование цепи на туннельном диоде

Моделирование цепи на туннельном диоде

А теперь займемся моделированием явно нелинейной цепи. Выполним его для цепи, которая состоит из последовательно включенных источника напряжения Es, резистора Rs, индуктивности L и туннельного диода, имеющего N-образную вольтамперную характеристику (ВАХ). Туннельный диод обладает емкостью С, что имитируется конденсатором С, подключенным параллельно туннельному диоду. Пусть ВАХ реального туннельного диода задана выражением:

> restart:

> A:=.3t: а:=10: В:=1*10^(-8): b:=20:

> Id:=Ud->A*Ud*exp(-a*Ud)+B*(exp(b*Ud-D):

Id:=Ud->AUde^(-aUd)+Be^(bUd-1)

Построим график ВАХ:

> plot(Id(Ud), Ud=-.02..0.76,color=black):

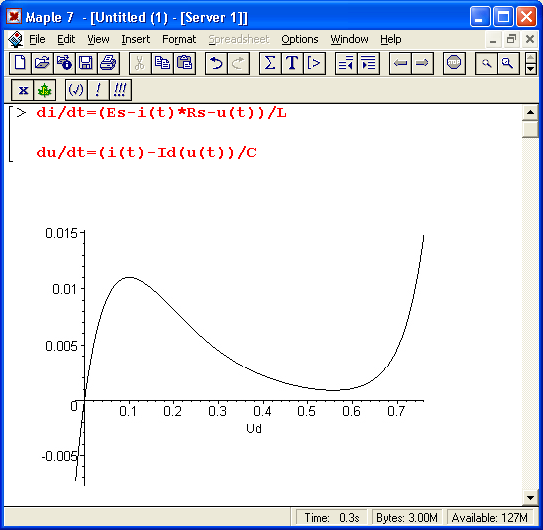
Этот график представлен на рис. 17.25. Нетрудно заметить, что ВАХ туннельного диода не только резко нелинейна, но и содержит протяженный участок отрицательной дифференциальной проводимости, на котором ток падает с ростом напряжения. Это является признаком того, что такая цепь способна на переменном токе отдавать энергию во внешнюю цепь и приводить к возникновению колебаний в ней различного типа.

Работа цепи описывается системой из двух дифференциальных уравнений:

di/dt=(Es-i(t)*Rs-u(t))/L

du/dt=(i(t)-Id(u(t))/C

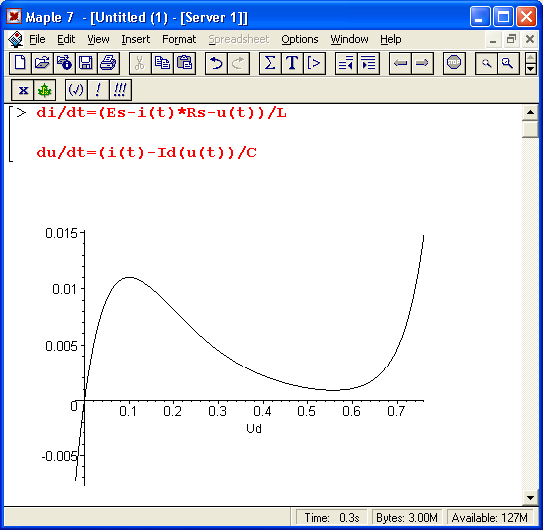
Рис. 17.25.ВАХ туннельного диода

Пусть задано Es = 0,35 В, Rs= 15 Ом, С = 10*10-12, L = 30*10-9 и максимальное время моделирования tm=10*10-9. Итак, задаем исходные данные:

> Es:=.35:Rs:=15:C:=10*10^(-12):L:=30*10^(-6):tm:=10*10^(-9):

Составим систему дифференциальных уравнений цепи и выполним ее решение с помощью функции dsolve:

Поскольку заведомо известно, что схема имеет малые значения L и С, мы задали с помощью параметров достаточно малый шаг решения для функции dsolve — stepsize=l(T(-11) (с). При больших шагах возможна численная неустойчивость решения, искажающая форму колебаний, получаемую при моделировании. Используя функции odeplot и displ ay пакета plots, построим графики решения в виде временных зависимостей u(t) и 10*i (t) и линии, соответствующей напряжению Es источника питания:

> gu:=odeplot(F,[t,u(t)],0,tm,color=black,

labels=['tVu(t),10*i(tr]):

> gi:=odeplot(F,[t,10*i(t)],0..tm.color-black):

> ge:=odeplot(F,[t,Es].0..tm.color=red): .

> display(gu.gi,ge);

Эти зависимости представлены на рис. 17.26. Из них хорошо видно, что цепь создает автоколебания релаксационного типа. Их форма сильно отличается от синусоидальной.

Рис. 17.26.Временные зависимости напряжения на туннельном диоде и тока

Решение можно представить также в виде фазового портрета, построенного на фоне построенных ВАХ и линии нагрузки резистора Rs:

> gv:=plot({Id(Ud),(Es-Ud)/Rs},Ud=-.05..0.75,color=black,

labels=[Ud,Id]):

> gpp:=odeplot(F.[u(t),i(t)],0..tm,color=blue):

> display(gv,gpp);

Фазовый портрет колебаний показан на рис. 17.27.

Рис. 17.27.Фазовый портрет колебаний на фоне ВАХ туннельного диода и линии нагрузки резистора Rs

О том, что колебания релаксационные можно судить по тому, что уже первый цикл колебаний вырождается в замкнутую кривую — предельный цикл, форма которого заметно отличается от эллиптической.

Итак, мы видим, что данная цепь выполняет функцию генератора незатухающих релаксационных колебаний. Хотя поставленная задача моделирования цепи на туннельном диоде успешно решена, в ходе ее решения мы столкнулись с проблемой обеспечения малого шага по времени при решении системы дифференциальных уравнений, описывающих работу цепи. При неудачном выборе шага можно наблюдать явную неустойчивость решения.

55.gif

56.gif

57.gif

58.gif

20. Применение интеграла Дюамеля для расчета переходных процессов

Применение интеграла Дюамеля для расчета переходных процессов

Вернемся к линейным цепям и рассмотрим еще один полезный метод расчета электрических цепей — с помощью интеграла Дюамеля. При нем можно рассчитать временную зависимость выходного напряжения u2(t) цепи по известному входному сигналу ul(t) и переходной характеристике цепи a(t). Возьмем в качестве первого классического примера дифференцирующую RC-цепь и вычислим ее реакцию на экспоненциально нарастающий перепад напряжения.

Представлены заданные зависимости ul(t) и a(t), аналитическое выражение для интеграла Дюамеля (одна из 4 форм) и аналитическое выражение для искомой зависимости u2(t). Пока последнее выражение довольно простое. В конце этого фрагмента документа построены графики зависимостей ul(t), a(t) и u2(t).

Обратите внимание на то, что выражение для u2(t), получаемое с помощью интеграла Дюамеля, стало намного сложнее. Тем не менее получено как аналитическое выражение для реакции цепи u2(t), так и графики ul(t), a(t) и u2(t). Они показаны внизу графика.