Товарооборот и издержки обращения, тыс. Руб.

Порядковый номер, - i	Товарооборот -	Издержки обращения -
1	480	30
2	510	25
3	530	31
4	540	28
5	570	29
6	590	32
7	620	36
8	640	36
9	650	37
10	660	38

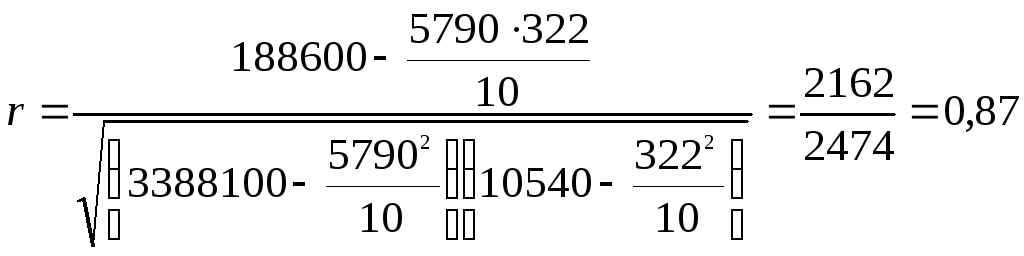
Таблица 1.11.4

Расчетные показатели

i
1	480	30	230400	900	14400
2	510	25	260100	625	12750
3	530	31	280900	961	16430
4	540	28	291600	784	15120
5	570	29	324900	841	16530
6	590	32	348100	1024	18880
7	620	36	384400	1296	22320
8	640	36	409600	1296	23040
9	650	37	422500	1369	24050
10	660	38	435600	1444	25080
	5790	322	3388100	10540	188600

Проверим найденное значение коэффициента на значимость:

1) вычислим эмпирическое значение критерия: ;

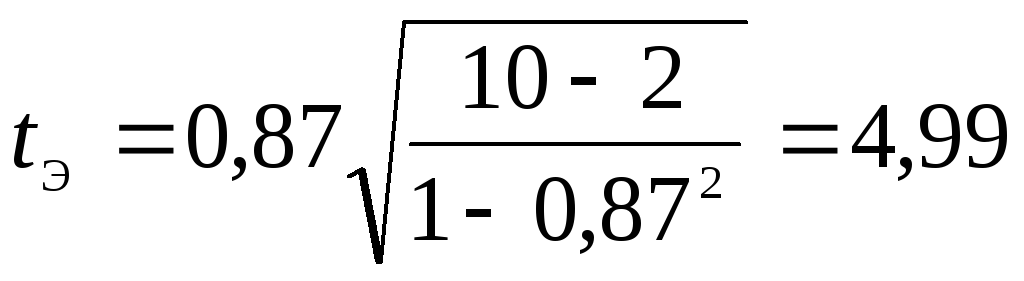2) по уровню значимости: и числу: v=8 в табл. П4 находим критическое значение: .

Так как 4,99 > 2,306, то с вероятностью 0,95 можно утверждать, что зависимость издержек обращения от товарооборота является прямой и сильной (табл. 1.11.1).

Упражнение 1.11.1. По следующим данным постройте поле корреляции и, предполагая зависимость между признаками х и y линейной, оцените связь между ними.

х	1	4	7	11	15	17	22
y	3	6	10	14	18	24	30

1.11.4. Регрессионные модели парной корреляции

Регрессионной моделью парной корреляции называется уравнение

, (1.11.3)

где f – некоторая математическая функция;

– параметры;

– значения фактора х;

– теоретические значения результативного признака, рассчитанные по формуле (1.11.3).

Значения параметров модели (1.11.3) определяются методом наименьших квадратов (МНК). Поэтому они называются МНК-оценками параметров. Для вычисления МНК-оценок параметров модели (1.11.3) надо:

1) записать функцию

, (1.11.4)

где n – число наблюдений;

2) вычислить первые частные производные функции (1.11.4) по параметрам и приравнять их к нулю;

3) решить полученную систему уравнений, называемую систему нормальных уравнений.

Решения системы нормальных уравнений являются искомыми МНК-оценками параметров.

Основной предпосылкой для построения регрессионной модели парной корреляции является близость распределения значений результативного признака к нормальному распре­делению.

Регрессионной моделью линейной корреляции является линейная модель

, i=1,...,n. (1.11.5)

Выведем формулы для вычисления МНК-оценок параметров линейной модели:

1) функция (1.11.4) для линейной модели имеет вид:

; (1.11.6)

2) дифференцируя функцию (1.11.6) по параметрам и и приравнивая полученные производные нулю, получим систему нормальных уравнений

,

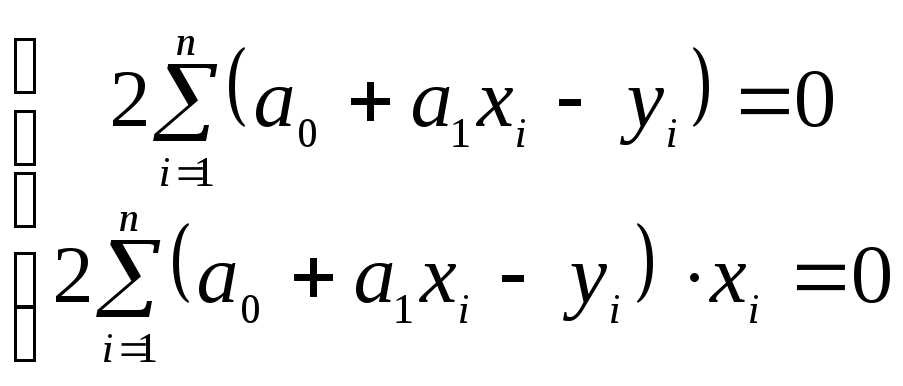равносильную системе уравнений

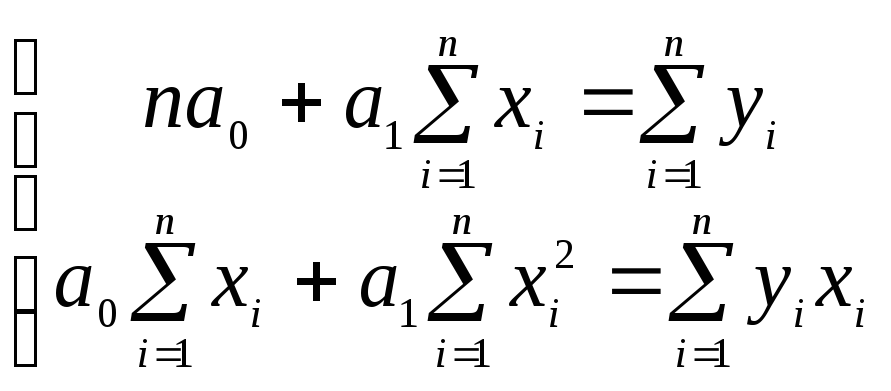. (1.11.7)

3) решаем систему (1.11.7) по формулам Крамера:

,

,

,

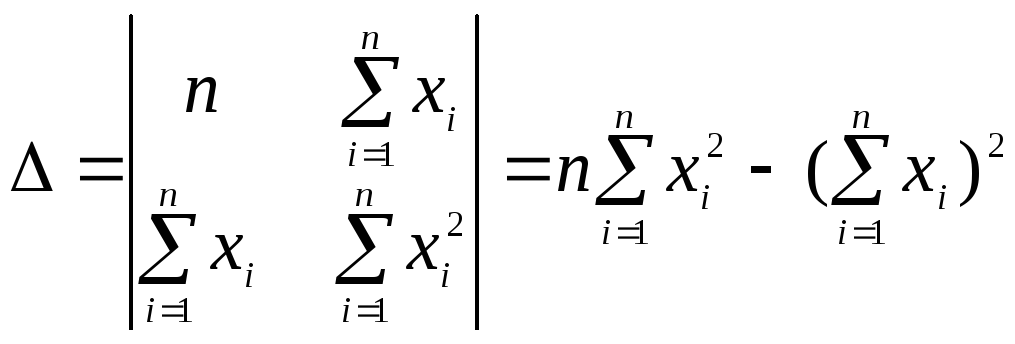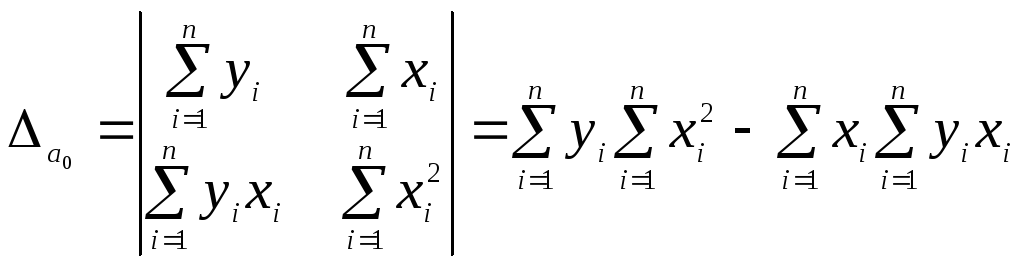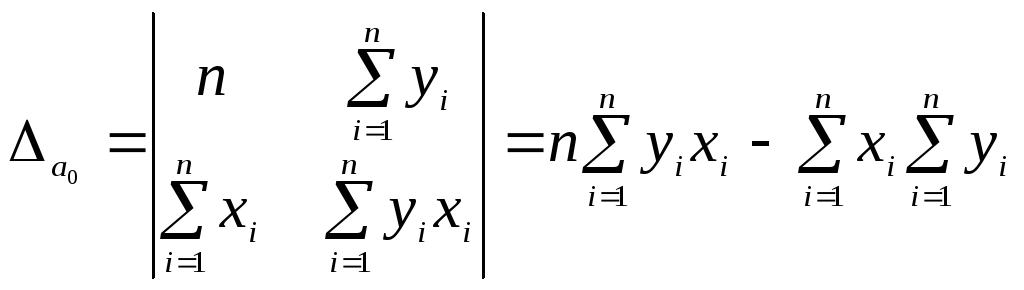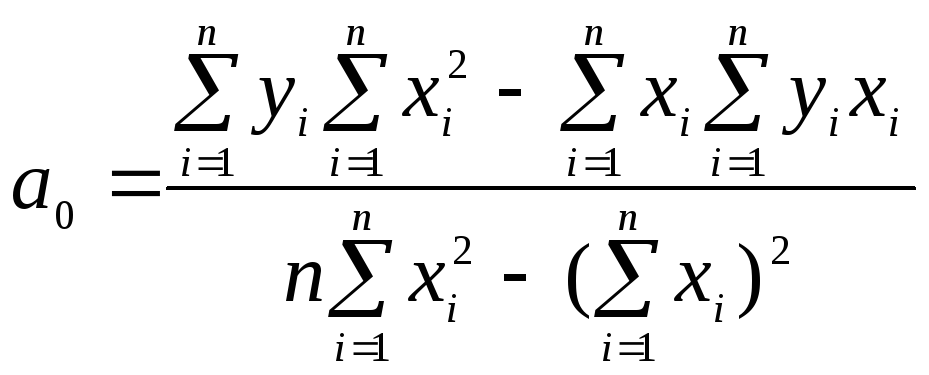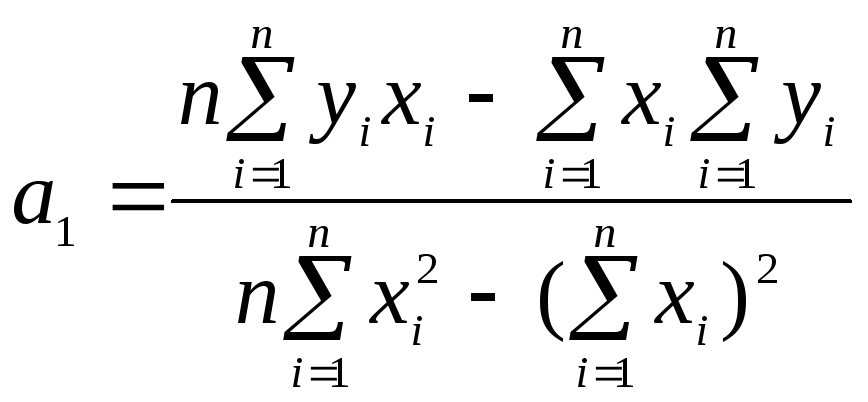, . (1.11.8)

МНК-оценки параметров модели (1.11.5) вычисляются по формулам (1.11.8).

Заметим, что модель (1.11.5) можно записать в матричной форме

, (1.11.9)

где Т – знак транспонирования матицы;

; ; .

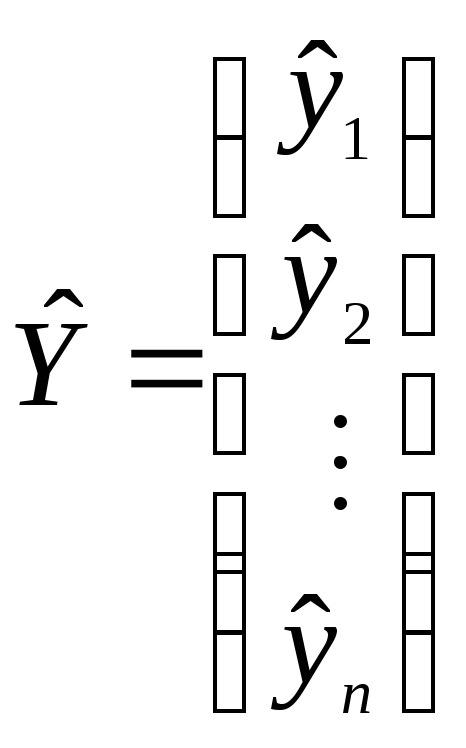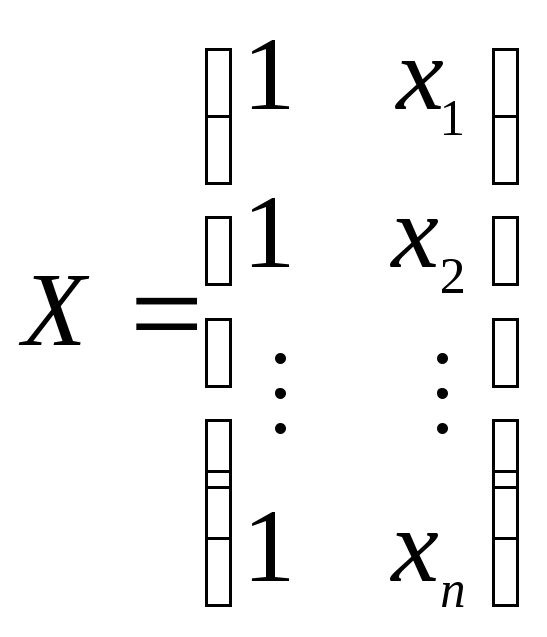Докажем, что МНК-оценки параметров линейной модели можно вычислить по формуле

, (1.11.10)

где

.

Вычислим матрицу :

=,

,

=,

==

=.

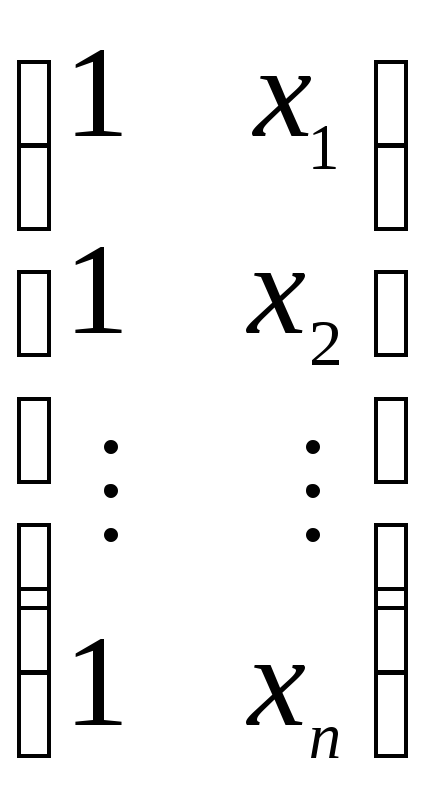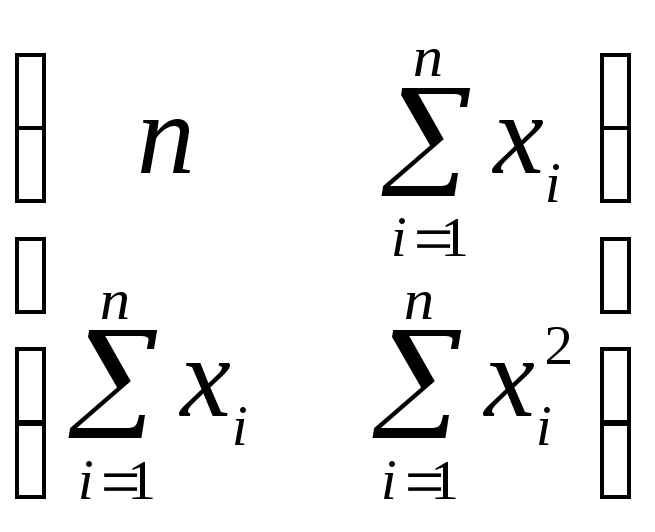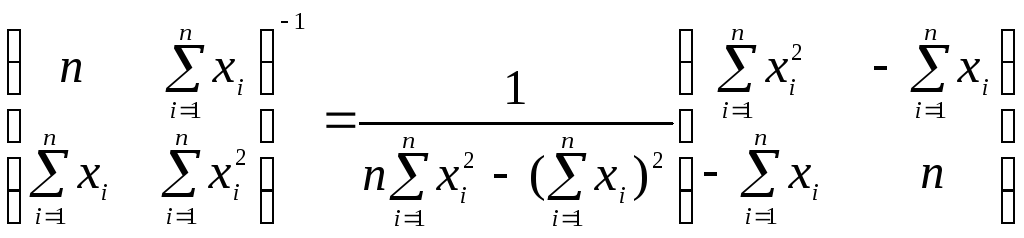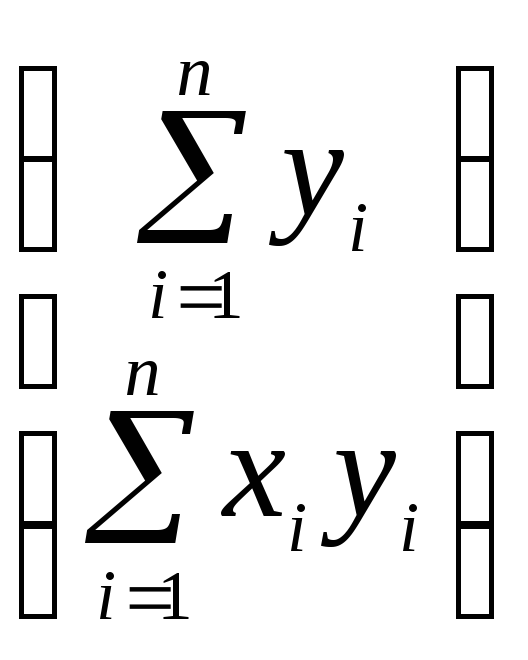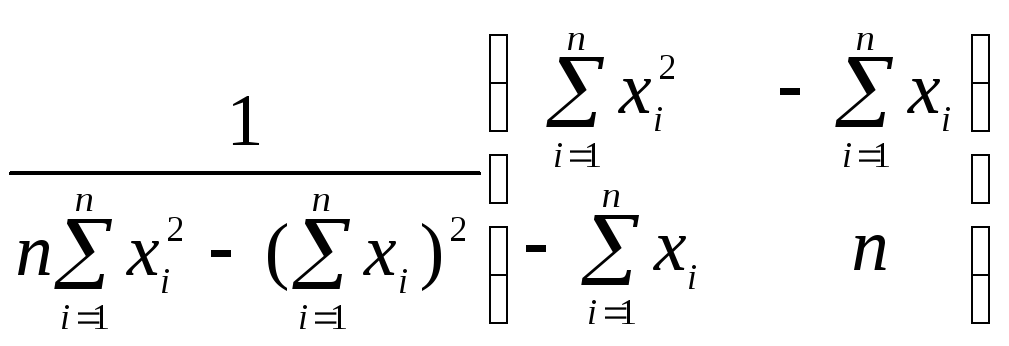
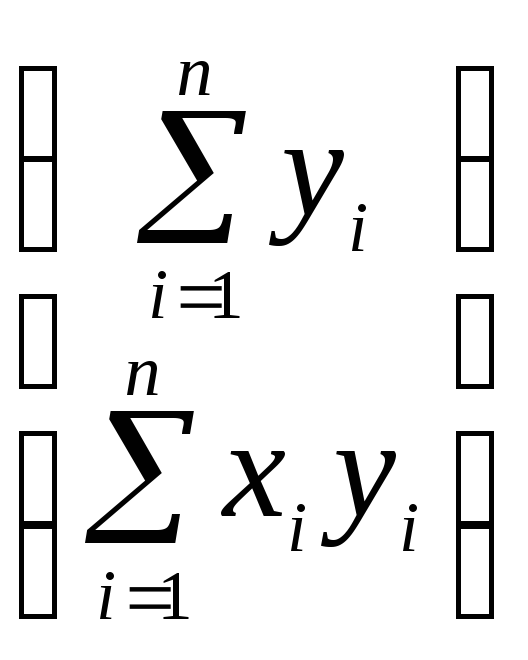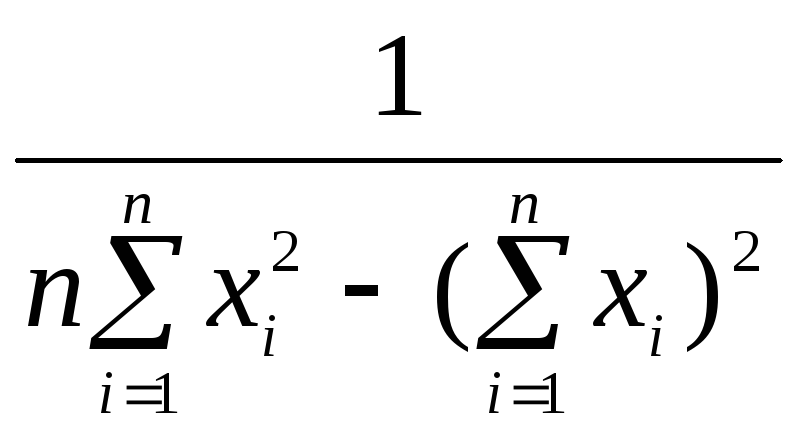
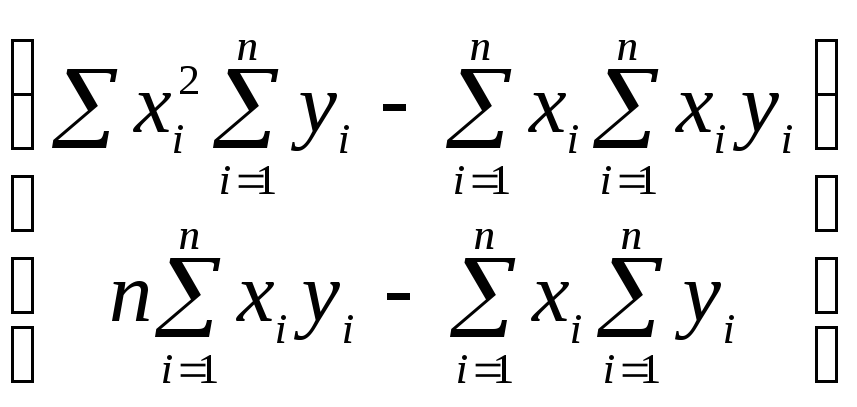В правой части последнего равенства записаны формулы (1.11.8) в матричной форме.

Для анализа нелинейных корреляций применяют нелинейные регрессионные модели. Рассмотрим наиболее употребительные из них.

1. Полулогарифмическая модель: .

Эта модель является линейной относительно . Поэтому МНК-оценки параметров полулогарифмической модели вычисляются по формулам

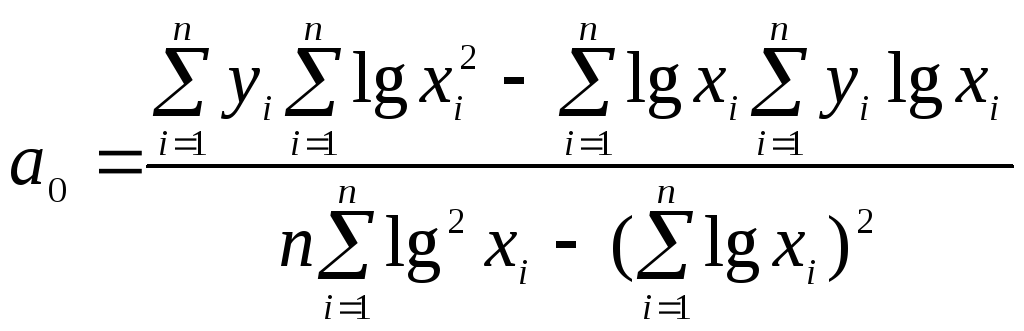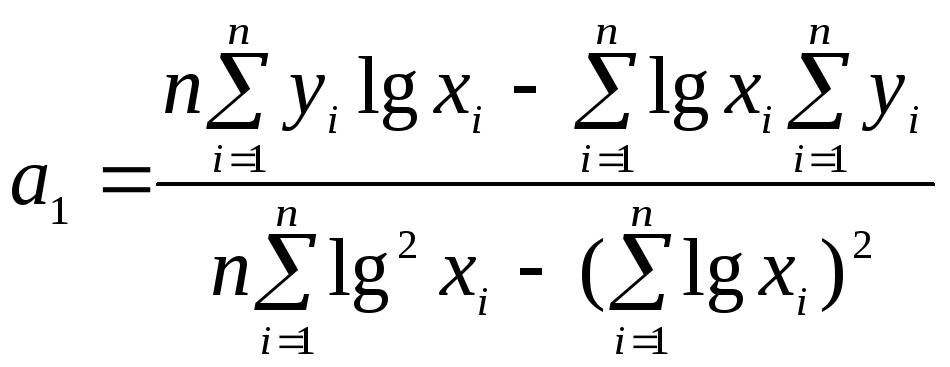, . (1.11.11)

2. Экспоненциальная модель: .

Логарифмирование обеих частей модели приводит к линейной модели . Поэтому МНК-оценки параметров экспоненциальной модели вычисляются по формулам

, ;

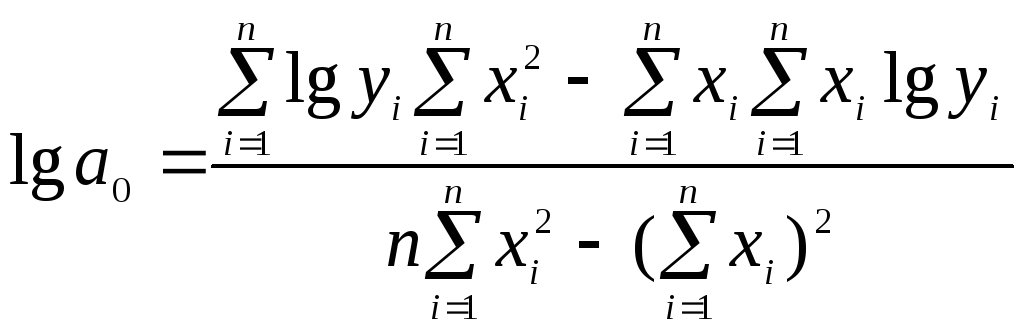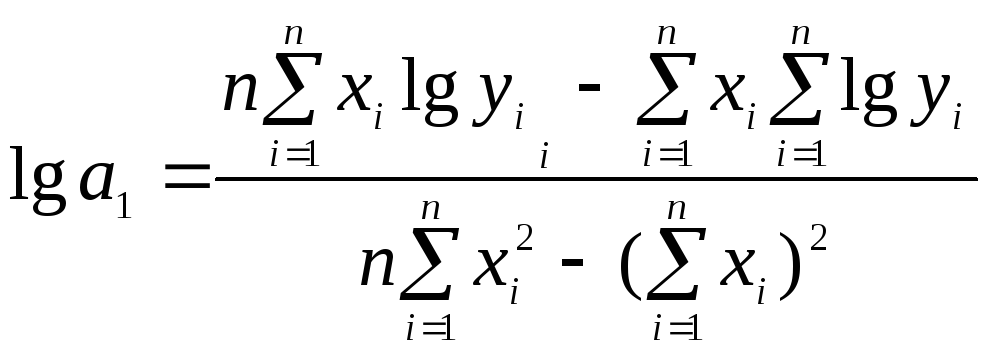, . (1.11.12)

3. Гиперболическая модель: .

Так как эта модель является линейной относительно , то МНК-оценки параметров гиперболической модели вычисляются по формулам

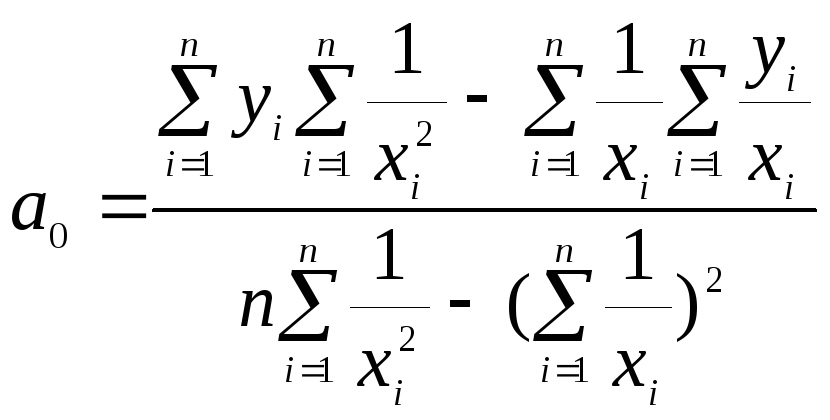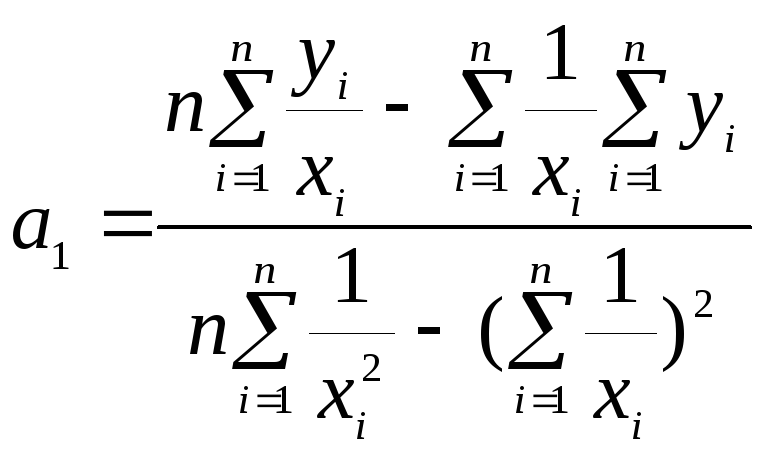, . (1.11.13)

1. Параболическая модель: .

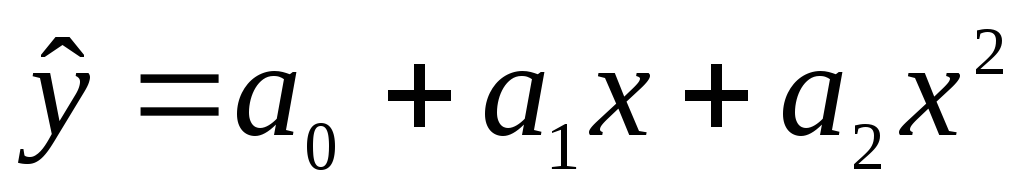Функция (1.11.4) для параболической модели имеет вид

. (1.11.14)

Дифференцируем функцию (1.11.14) по параметрам , и и приравниваем полученные производные к нулю. Получим систему нормальных уравнений

,

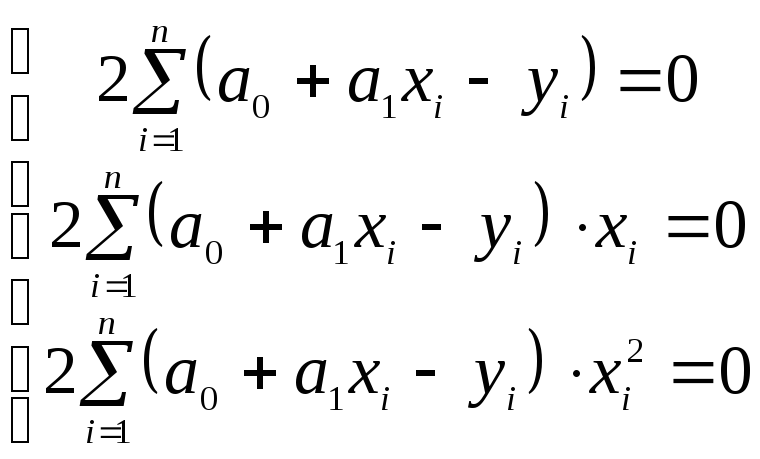равносильную системе уравнений

. (1.11.15)

Решения системы (1.11.15) являются МНК-оценками параметров параболической модели.

Если линейная модель построена по малой выборке (), то МНК-оценки параметров и проверяются на значимость по правилу:

1) вычислить эмпирические значения для параметров и соответственно по формулам

и , (1.11.16)

где

и ; (1.11.17)

2) найти в табл. П4 по уровню значимости  и чис­лу критическое значение ;

Если , то с вероятностью значения параметров и признаются значимыми.

Параметр линейной модели показывает, на сколько единиц изменяется значение результативного признака при увеличении фактора на одну единицу.

Коэффициент эластичности

, (1.11.18)

где  среднее значение фактора;

 среднее значение результативного признака;

 параметр линейной модели,

показывает, на сколько процентов в среднем изменяется результативный признак при изменении фактора на 1%.

Адекватность регрессионной модели оценивается с помощью средней ошибки аппроксимации (приближения), вычисляемой по формуле

(1.11.19)

Модель признается адекватной, если ее ошибка (1.11.19) не превышает 15%.

В случае нелинейной корреляции коэффициент k, рассмотренный в 1.11.2, называется индексом корреляции, обозначается через R и вычисляется по формуле

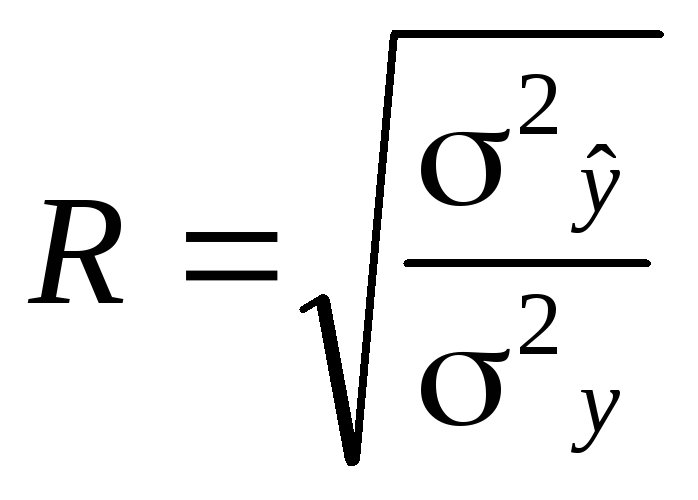, (1.11.20)

где – общая дисперсия результативного признака

; (1.11.21)

– факторная дисперсия результативного признака

. (1.11.22)

Разность: равна остаточной дисперсии

. (1.11.23)

Дисперсии , и характеризуют вариацию признака y , обусловленную влиянием соответственно всех факторов, фактора х и всех факторов, кроме фактора х. Из равенства: + следует, что индекс корреляции (1.11.19) можно вычислить также по формуле

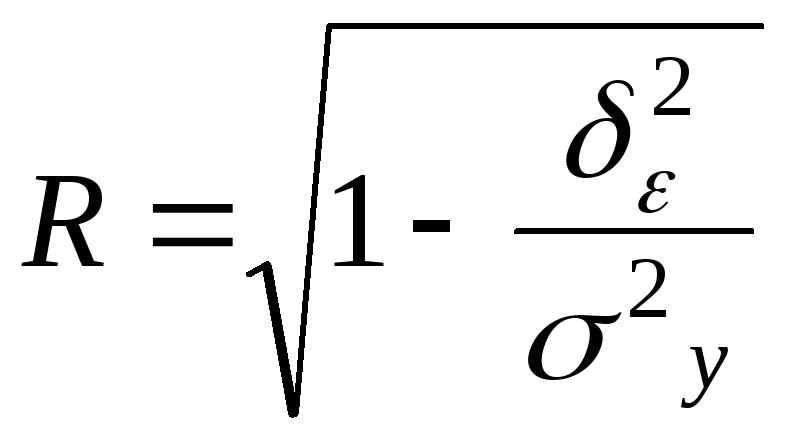. (1.11.24)

Если фактор х не влияет на вариацию признака y, то факторная дисперсия равна 0 и, следовательно, индекс корреляции равен 0. В случае, когда на вариацию признака y влияет только фактор х, факторная дисперсия совпадает с общей дисперсией и индекс корреляции равен 1. Так как , то .

Заметим, что линейный коэффициент корреляции совпадает с индексом корреляции только в случае линейной корреляции.

В случае малой выборки значение индекса корреляции проверяется на значимость по следующему правилу:

1) вычислить эмпирическое значение

, (1.11.25)

где т — число параметров уравнения регрессии;

2) в табл. П5 по уровню значимости  и числам и найти критическое значение критерия .

Если , то с вероятностью значение индекса корреляции признается значимым.

Число , выражающее долю факторной дисперсии в общей дисперсии, называется индексом детерминации (причинности). Чем ближе индекс детерминации к 1, тем точнее модель описывает корреляцию. Если индекс корреляции R превышает 0,7, то более половины общей вариации результативного признака объ­ясняется влиянием учитываемого фактора х.

Пример 1.11.2. Продолжительность эксплуатации (возраст) оборудования и затраты на его ремонт приведены в табл. 1.11.5.

Таблица 1.11.5