58. Лінеаризація задачі опуклого програмування. Теорема Куна-Танкера. Умови Куна-Таккера

Лінеаризація задачі опуклого програмування

Математичне формулювання задачі опуклого програмування, яка піддається лінеаризації, можна записати у вигляді

		(8.97)
— нелінійна функція,			(8.98)

Апроксимацію функції цілі порівняно просто можна здійснити тільки в тому випадку, коли вона залежить нелінійно від небагатьох компонентів вектора. У задачах електроенергетики звичайно розгля­дається тільки випадок, коли нелінійність залежить від одного компо­нента

		(8.99)

де — лінійна частина функції – ЇЇ нелінійна частина, яка звичайно задається у чисельному вигляді (таблицею чи графіком) у координатах _.

Припустимо, що задана у вигляді монотонної функції зі спад­ною похідною. Здійснимо її лінеаризацію однією прямою, проведеною між точками та , які відповідають крайнім точкам апроксимованої кривої (символами позначені числові значення абсцис, тобто ; символами – числові значення ординат, тобто ).

Абсцису можна зобразити як лінійну функцію деяких двох змін­них, зокрема як

(8.100)

Для однозначності наведеного співвідношення накладемо умову

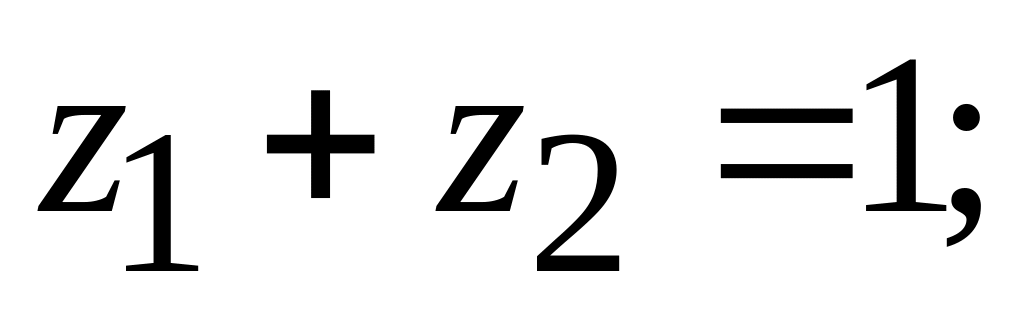
(8.101)

в (8.100) і (8.101) знаходимо

(8.102)

При зміні від до змінюється від до . Отже, вираз (8.102) слід розглядати саме в такому інтервалі.

_{Запишемо рівняння прямої, що проходить через точки та тобто рівняння апроксимованої функції}

Підставляючи в одержаний вираз значення з (8.102), маємо

(8.103)

чи

(8.104)

Далі, перемножуюєм на рівняння (8.101):

(8.105)

Підставляючи (8.105) у (8.104), одержуємо рівняння апроксимуючої функції

(8.106)

Отже, для лінеаризованої задачі рівняння (8.97) і (8.106) у розгорненій формі мають вираз

(8.107)

(8.108)

Скориставшись наведеним способом, можна дістати апроксимацію кривої декількома прямими, тобто здійснити кусково-лінійну апроксимацію на багатьох інтервалах.

Необхідно підкреслити, що такий метод зведення задачі неліній­ного програмування до лінійного справедливий тільки для монотонних функцій . Причому зі спадною похідною можна апроксимувати лише у випадку максимізації цільової функції , а зі зростаючою похідною – лише при мінімізації цільової функції.

Теорема Куна-Танкера. Умови Куна-Таккера

Ця теорема є узагальненням методу неозначених множників Лагранжа для екстремальних задач з умовами обмеження у вигляді нерів­ностей і стосується загальної задачі опуклого програмування

(8.111)

Теорема Куна–Таккера ґрунтується на понятті сідлової точки – точки,в околі якої значення цільової функції збільшується по одних напрям ахі зменшується по інших (для двовимірної функції рис. 8.18 відповідає точці ). Для її визначення користуються функцією Лагранжа

Теорема стверджує: пара векторів та відповідають сідловій точці функції в облас­ті для всіх та якщо задовольняється умова

(8.112)

Співвідношення (8.112) можна ще записати як

(8.1130

Остання умова відповідає мінімізації функції Лагранжа по змінній і максимізації по змінній .Шукане розв'язаннявизначає сідлову точку. У тривимірному просторі з координатами сідлова точка в геометричній інтерпретації відповідає увігнутій цільовій функції по координаті (при вона мяє мінімум) і опуклій цільо­вій функції по координаті (при вона має максимум, див. рис. 8.17).

Таким чином, задача знаходження сідлової точки функції зводиться до знаходження точки , яка відповідає (8.113).

Отже, з теореми Куна–Таккера випли­ває, що розв'язання задачі (8.111) зводиться до знаходження сідлової точки для функції Лагранжа. Оскільки умови відповідають вимозі мінімізації по одній змінній і максимізації по іншій, то їх можна записати ще в такому вигляді:

							(8.114)
					(8.115)
						(8.116)
					(8.117)

Умови КунаТаккера (8.114) – (8.117) необхідні та достатні для розв'язування задачі опуклого програмування. їх можна інтерпрету­вати наступним чином. Оскільки сідлова точка мінімізуюча відносно кожної змінної то вона не може збігатися з точкою, у якій тому що функція могла б зменшуватися зі збільшенням . Отже, у сідловій точці (умова 8.114). Але за умови (8.114) змінна досягає свого найменшого значення, тобто Що й стверджує умова (8.115).

Так само в силу того, що сідлова точка повинна бути максимізую чому по кожній змінні , нерівність неможлива, тому що функція збільшувалася б і далі. Таким чином (умова (8.116)) і строга нерівність має місце лише тоді, коли змінна зменшується до нуля (умова (8.117)).

Теорема Куна—Таккера не дає алгоритму розв'язання задачі, а лише встановлює умови, за яких таке розв'язання має місце.