§5.Неприводимые представления группы трансляций

Для рассмотрения представлений группы трансляций воспользуемся циклическими граничными условиями, т.е. будем считать, что после трансляции на +1 периодов трансляция совпадёт с трансляцией , т.е.

.

Произвольный элемент группы трансляций можно записать в виде

.

Все трансляции коммутируют друг с другом и, следовательно, группа трансляций абелева.

Группу трансляций можно рассматривать как прямое произведение трёх циклических групп с элементами . Неприводимые представления циклической группы одномерны. Такие представления группы , имеющие порядок , определяются числами , где m - номер неприводимого представления, , а n- степень соответствующего элемента циклической группы. Следовательно, неприводимые представления группы трансляций с элементами имеют вид

.

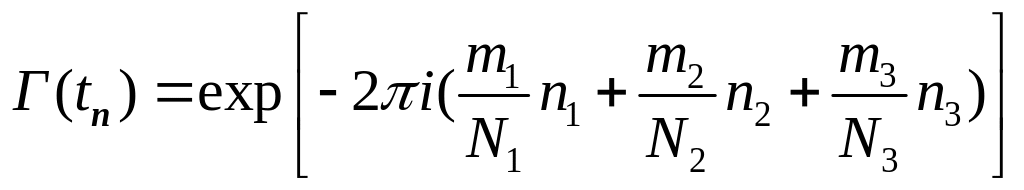Таким образом, каждое неприводимое представление группы определяется тройкой чисел , а число различных неприводимых представлений равно произведению . Определим тройку векторов соотношениями

.

Решение этой системы относительно неизвестных векторов b приводит к такому результату:

,

где везде в числителе стоит в квадратных скобках векторное произведение, а объём параллелепипеда, построенного на трёх базисных векторах a. Легко видеть, что размерность векторов b обратная по отношению к размерности векторов a, поэтому эти вектора называют векторами обратной решётки (по отношению к решетке, определяемой векторами a). С помощью обратных векторов введём новый вектор

,

С вектором неприводимые представления группы трансляций на вектор могут быть записаны в виде

.

Два вектора и в обратном пространстве различающиеся на вектор

,

где - целые положительные и отрицательные числа, включая ноль, называются эквивалентными и характеризуют одно и то же представление. Вектора называются векторами обратной решётки. В качестве области изменения вектора , удобно выбрать такую односвязную область, которая содержит в себе начало координат и для которой выполняются следующие условия:

а) эта область не содержит эквивалентных векторов;

б) для произвольного вектора обратной решётки в этой области найдётся эквивалентный вектор.

Эта область называется приведённой зоной Бриллюэна. Если вектор лежит на границе зоны Бриллюэна, то всегда существует, по крайней мере, один эквивалентный ему вектор , также лежащий на границе зоны Бриллюэна.

Нетрудно проверить, что симметрия прямой и обратной решёток совпадают.

§5.Конкретные примеры прямой и обратной решёток

1) Прямые решётки.

Как было отмечено в п.2 элементарную ячейку решётки Браве, а, следовательно, и рассматриваемый кристалл, можно описать с помощью трёх некомпланарных векторов a,b,c, направленных вдоль рёбер соответствующего параллелепипеда. Однако удобнее выбрать векторы элементарной ячейки таким образом, чтобы она явно обладала симметрией решётки Браве.

Предположим, что некоторая точка структуры есть центр симметрии, тогда и все эквивалентные точки обладают этим свойством. Такую точку можно выбрать в качестве центра ячейки; при этом сама ячейка будет центрально симметричной. Теперь можно предложить регулярный приём построения ячеек, центрированных таким образом и называемых ячейками Вигнера-Зейтца.

Здесь мы рассмотрим один случай, который иллюстрирует многие основные закономерности и, кроме того, представляет самостоятельный интерес, поскольку эта структура действительно реализуется в кристаллах некоторых химических элементов. Мы обсудим кубическую объёмноцентрированную решётку (рис. а).

Она на первый взгляд представляет собой кубическую решётку с двумя атомами в элементарной ячейке или две взаимопроникающие простые кубические подрешётки, определяемые равенствами

,

,

где - целые числа.

Если, однако, мы напишем

, , ,

то векторы всех точек будут записаны так ,

где - целые числа. Если сумма нечётная, то мы попадаем в центр куба, если чётная – в его вершины. Таким образом (см. рис. б), это действительно решётка Браве.

В место кубической элементарной ячейки можно рассмотреть ячейку Вигнера - Зейтца; для её построения нужно «отрубить» (см. рис. в) вершины куба на половине их расстояния до центра. Получаемая фигура имеет, очевидно, ту же симметрию, что и куб.

Рассмотрим теперь гранецентрированную кубическую решётку. Она строится из четырёх взаимопроникающих простых кубических решёток, расположенных таким образом, что если мы посмотрим на одну из них, то увидим узлы, как в центре каждой грани её элементарной ячейки, так и вершинах куба (см. рис. а)

Эта структура, если выбрать векторы в качестве базисных, как и в объёмноцентрированной решётке, будет иметь четыре узла в элементарной ячейке. Однако если в качестве базисных векторов выбрать половины диагоналей граней куба

,

где a-длина ребра куба (постоянная решётки), то линейная комбинация этих векторов с целочисленными коэффициентами может определить любой узел решётки.

Поэтому фактически гранецентрированная решётка есть решётка Браве с выше приведённой тройкой базисных векторов.

2. Обратные решётки. Допустимые значения векторов , нумерующих неприводимые представления группы трансляций, отстоят друг от друга, как видно из формулы, на расстоянии в направлении . Но - порядка , а - длина стороны образца. Таким образом, набор значений вектора определяется не только структурой кристалла, но и зависит от размеров образца. В обратном пространстве объём вокруг каждой точки из данного набора равен

,

где произведение в числителе является объёмом ячейки обратной решётки.

Тождество .

Позволяет записать формулу для плотности векторов в единице объёма обратного пространства

,

где V- объём кристалла.

Для бесконечного кристалла наш набор дискретных точек в ячейке обратной решётке расплылся бы в континуум.

Геометрические свойства обратной решётки могут быть столь же разнообразны, сколь и свойства прямой решётки, из которой она была получена. Отметим здесь такое обстоятельство. Воспользуемся базисными векторами гранецентрированной кубической решётки и построим базисные векторы обратной решётки. Несложные алгебраические преобразования приведут нас к такому результату:

.

Решётка образованная этими векторами,- объёмноцентрированная кубическая.

Наоборот, обратной решёткой для объёмноцентрированной кубической решётки является решётка гранецентрированная кубическая.

Мы уже вводили понятие приведённой зоны Бриллюэна - элементарной ячейки обратного пространства. Можно говорить, что зоной Бриллюэна является ячейка Вигнера - Зейтца для обратного пространства. Приведём их для обсуждавшихся выше, кубических решёток (ОЦК) и (ГЦК) соответственно.

В терминах общего тензорного исчисления базис прямой решётки называется ковариантным базисом, а базис обратной решётки - контравариантным. Нетрудно показать, что каждый из векторов обратной решётки ортогонален некоторой плоскости, образованной узлами основной решётки.