Задача 4.

Зависимость координат частицы от времени имеет вид:

x = bcos t, y = bsin t.

Здесь b>0 и >0 – константы.

Найти: радиус-вектор r(t), скорость v(t), ускорение a(t), а также их модули, скалярные произведения и объяснить полученный результат; найти уравнение траектории частицы и направление ее движения.

Решение.

Согласно определению:

r(t) = xe_x + ye_y = bcos te_x + bsin te_y

.

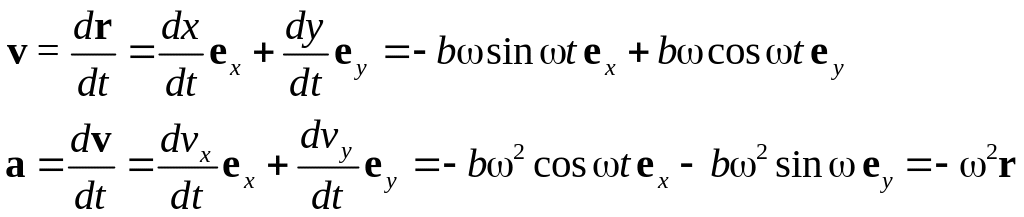Найдем модули векторов r, v и а:

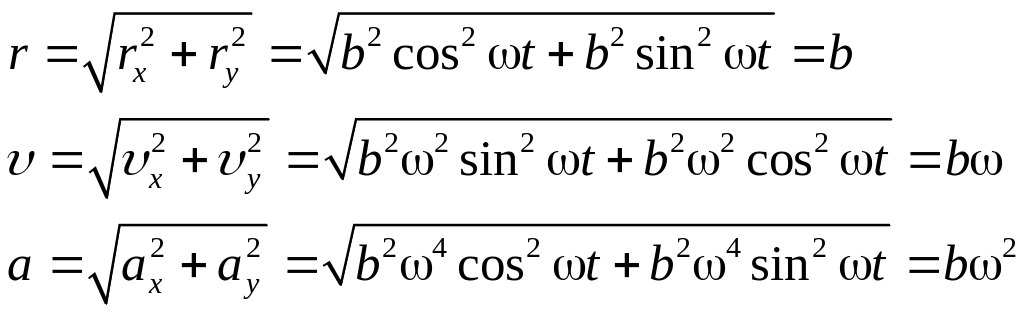
Найдём теперь скалярные произведения (r, v) и (r, a):

(r, v) = x_x + y_y = bcos t(– bsin t) + bsin t bcos t = 0,

(r, a) = – ² (r, r) = b²².

Как видим, векторы r и v взаимно перпендикулярны.

Поскольку а = – r, то а и r направлены в противоположные стороны, причем, вектор ускорения а направлен к началу координат. Траекторию можно определить двумя способами.

1. 

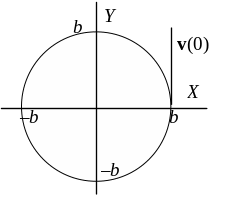
   Рис. 1

   способ. Так как координата частицы всё время и r = b = const, то траектория лежит в плоскости XOY и представляет собой окружность радиуса b с центром в начале координат.

2. способ. Так как х = bcos t, у = bsin t, то х² + у² = b².

Мы получили уравнение окружности радиуса R = b с центром в начале координат.

Найдем направление движения точки. При t = 0 частица находится в точке с координатами х = b, у = 0 и имеет скорость:

v(0) =_x(0)e_x + _y(0)e_y = 0e_x +be_y,

направленную вдоль оси OY. Т.е. движение происходит против часовой стрелки (см. Рис.1).

Если b<0, то направление движения изменяется на противоположное.

Задача 5

Колесо радиуса R катится без скольжения со скоростью V. Найти закон движения точки на ободе колеса, полагая в начальный момент t = 0 её координаты х = 0 и y = 0. Изобразить её траекторию, и указать направления скорости и ускорения.

Решение

За время t после начала движения центр колеса сместится на расстояние Vt, а само колесо повернётся вокруг оси на некоторый угол . Точка колеса А, которая в начальный момент находилась в начале координат, повернётся вместе с колесом. Угол  поворота колеса связан с перемещением центра колеса очевидным соотношением (см. Рис. 1), являющимся следствием, предполагаемого в условии, отсутствия скольжения:

Рис. 1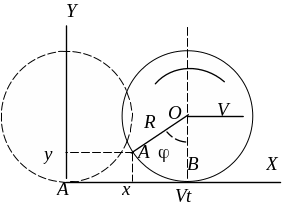

Vt = R (1).

Проще всего этот результат получить, если представить, что на обод колеса намотана лента, конец которой закреплён в начале координат. Если колесо откатится вправо на расстояние S = Vt, то с колеса смотается кусок ленты также длины S = Vt. С другой стороны, этот кусок ленты, будучи намотан на обод колеса, представляет собой дугу окружности, концы которой видны из центра колеса под углом  = S/R. Этот результат и доказывает справедливость (1).

Координаты точки А, как следует из рис. 1, равны:

x = R( – sin  ),

y = R(1 – cos ),

 = Vt/R.

Кривая, задаваемая этими соотношениями, называется циклоидой. Она изображена на Рис. 2.

Из найденного закона движения легко найти компоненты вектора v скорости точки A:

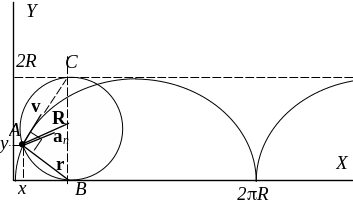
Рис. 2

В те моменты времени, когда y = 0, т.е. точка А оказывается в нижнем положении ( = 0, 2, 4, …), её скорость становится равной нулю. Что не удивительно, так как по условию проскальзывание отсутствует, отсутствие скольжения было "заложено" в соотношение (1) выше.

Подумайте сами, как изменится вид траектории, если колесо скользит. Здесь возможны два случая: скорость точки касания колеса с землёй направлена навстречу оси ОХ (так движется колесо автомобиля при езде на скользкой дороге), или наоборот – скорость точки касания направлена вперёд, т.е. в направлении оси ОХ. Это случай экстренного торможения автомобиля, когда он скользит по дороге.

Что касается направления вектора v скорости точки А, то этот вектор направлен из точки А в точку С, находящуюся в данный момент на самом верху колеса. Действительно, проведём из точки B касания колеса с осью ОХ в точку А вектор r. Его проекции на оси ОХ и ОY, очевидно, равны:

r_x = x – Vt = – R sin,

r_y = y = R(1 – cos).

Этот вектор r ортогонален вектору v скорости точки А, поскольку скалярное произведение этих векторов равно нулю:

(r,v) = r_x _x + r_y _y = – R sinV(1 – cos) + R(1 – cos)V sin = 0.

Вектор r – есть катет АВ прямоугольного треугольника АВС. Поскольку всякий прямоугольный треугольник вписанный в окружность имеет гипотенузой диаметр этой окружности, то ВС – диаметр колеса. Но точка В есть самая нижняя точка колеса, следовательно, С – самая верхняя его точка.

Этот результат можно получить и без вычислений, если заметить, что скорость точки соприкосновения колеса с осью ОХ равна нулю, поскольку колесо не скользит. Но это означает, что колесо в данный момент времени вращается вокруг этой точки. Следовательно скорость точки А направлена перпендикулярно радиус-вектору r. Всё остальное вытекает из этого факта.

Продифференцировав компоненты скорости по времени, найдём компоненты ускорения:

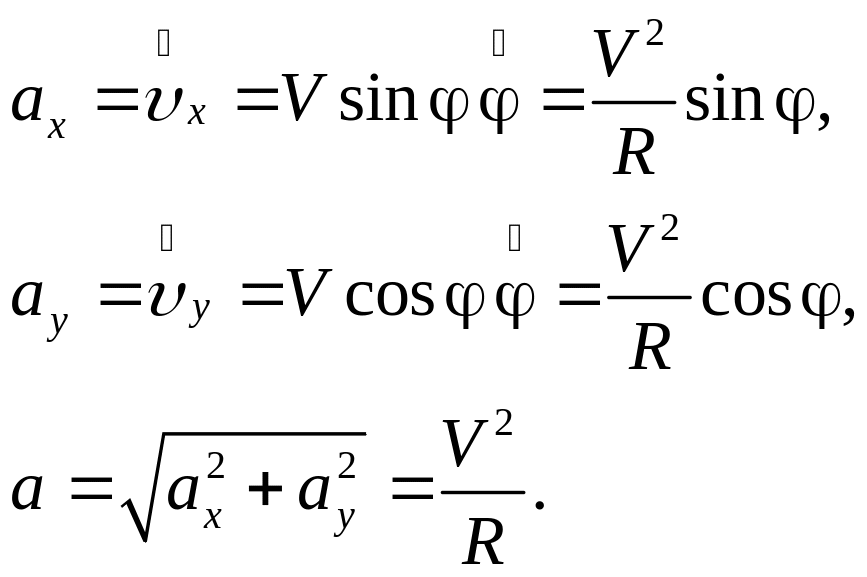
Нетрудно понять, что ускорение точки в любой момент времени направлено к центру колеса. Проще всего это сделать, перейдя в систему отсчёта, которая равномерно движется вместе с осью колеса. В этой системе отсчёта точка А движется равномерно со скоростью V по неподвижной окружности радиуса R. Тем самым ускорение точки А есть центростремительное ускорение, и направлено оно к центру колеса.

Вычисления очень просты. В этой системе отсчёта компонента скорости v_y остаётся неизменной, а v_x уменьшается на V:

Дифференцируя по времени, найдём компоненты ускорения:

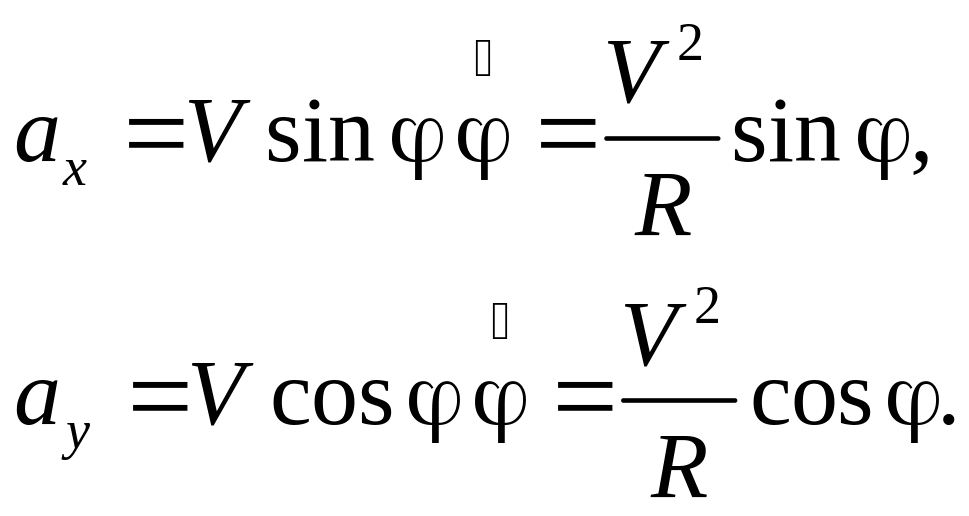
Сравнивая компоненты ускорения с проекциями радиус-вектора R:

R_x = x–R = –R sin ,

R_y = y – R = –Rcos ,

видим, что проекции этих векторов пропорциональны друг другу и отличаются знаками, т.е. вектор ускорения направлен навстречу вектору R (см. Рис. 2).

Задача 6

Спортсмены бегут колонной длины L со скоростью . Навстречу колонне бежит тренер со скоростью u<. Каждый из спортсменов, поравнявшись с тренером, поворачивает назад и продолжает бежать с прежней скоростью . Какой будет длина колонны L’ после того как последний спортсмен поравняется с тренером?

Решение

Решать задачу проще всего в системе отсчёта, связанной с тренером. В этой системе спортсмены приближаются к тренеру со скоростью  + u, а удаляются от него со скоростью  – u. Тогда время t, за которое колонна пробежит мимо тренера равно:

t = L/(  + u).

Но за это время голова колонны удалится от тренера на расстояние, равное новой длине колонны:

.

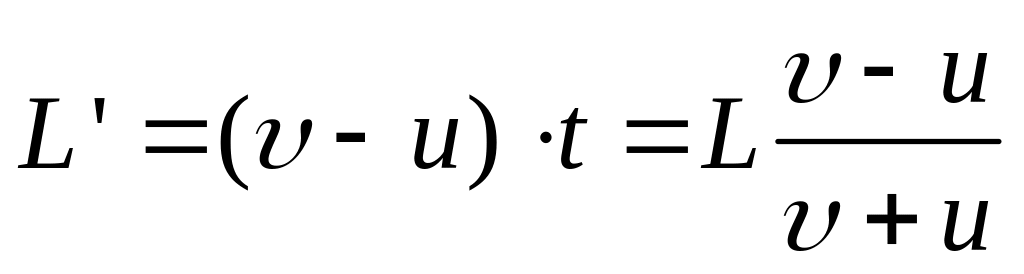Задача 7

Как показывают астрономические наблюдения, в видимой нами части Вселенной звёзды удаляются от Солнца со скоростями, пропорциональными расстоянию до Солнца: v = ar. Как будет выглядеть движение звёзд, если рассматривать его, находясь на какой–либо другой звезде?

Решение

Пусть Солнце расположено в точке О. Пусть в качестве новой системы отсчёта выбрана звезда О', положение которой относительно Солнца задаётся радиус–вектором R. Пусть, кроме того, мы наблюдаем за движением некоторой звезды А, положение которой относительно Солнца задаётся радиус–вектором r. Тогда положение этой же звезды относительно новой системы отсчёта задаётся радиус–вектором r' = r – R (см. Рис. 1). Тогда, согласно условию задачи, звезда А удаляется от Солнца со скоростью V=ar, а звезда О’ – со скоростью U = ar'. Согласно правилу сложения скоростей:

Рис. 1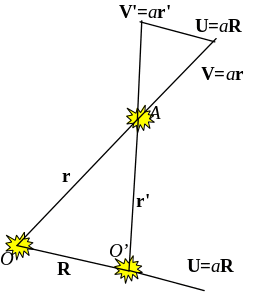

V = V' + U.

Следовательно, скорость V' звезды А относительно звезды О’ равна:

V' = V – U = a(r – R) = a r'.

Полученный результат означает, что и в новой системе отсчёта звёзды удаляются друг от друга со скоростями, пропорциональными расстоянию между ними.