Решение

Рис. 1

Пусть избыточное давление внутри мяча равно р. При соприкосновении мяча со стенкой мяч деформируется, и область соприкосновения представляет собой круг. Пусть радиус этого круга в некоторый момент равен r, величина деформации, соответственно х. Тогда эти величины связаны между собой (см. Рис. 1):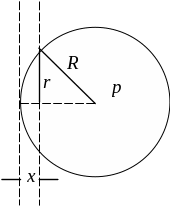

.

Здесь мы использовали условие слабого удара:

|x|<<R.

Площадь круга, в пределах которого мяч соприкасается со стенкой, равна:

S=r2 = 2Rx.

Сила давления со стороны мяча на стенку равна pS. С такой же силой, согласно третьему закону Ньютона, стенка действует на мяч:

F = – 2Rрx.

Как видим, сила является квазиупругой, поэтому движение мяча во время соприкосновения со стенкой будет гармоническим колебанием. Время удара  равно, очевидно, половине периода этого колебания:

.

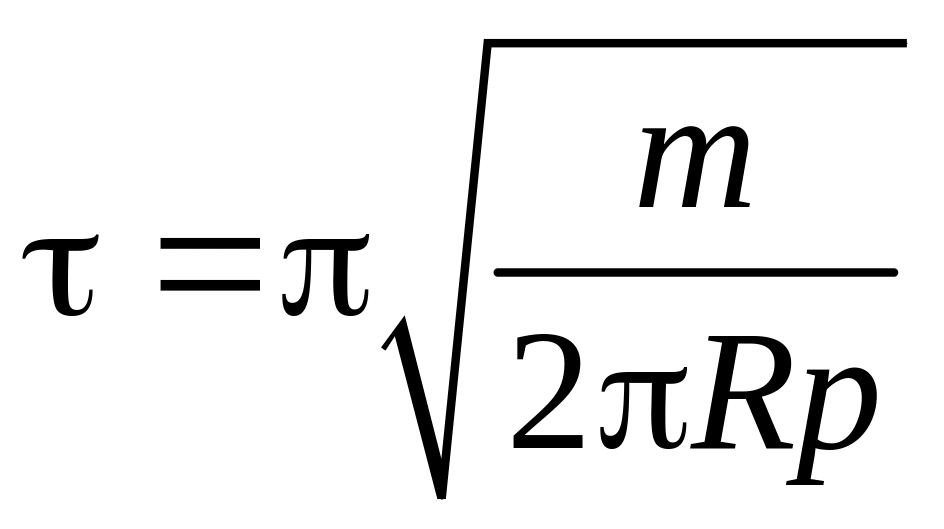Принимая массу мяча т = 0,4 кг, радиус R = 12 см, избыточное давление внутри мяча р = 10⁴ Па (0,1 атм), найдём:

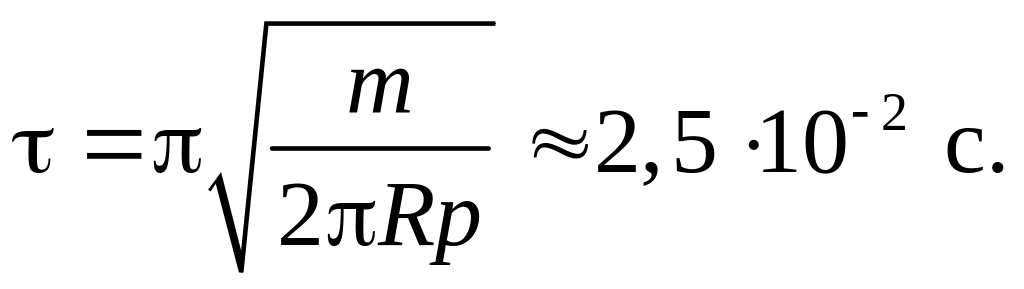
Задача 9

Рис. 1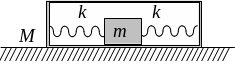

На гладком столе находится коробка массы М, внутри которой находится тело массы т. Это тело прикреплено к коробке двумя одинаковыми пружинами жёсткости k. Найти частоту колебаний этой системы пренебрегая силами трения.

Решение

Если груз сместится относительно стола на расстояние х, а коробка на расстояние Х, то левая пружина растянется на х – Х, а правая настолько же укоротится. Тем самым на груз будет действовать сила – k(х – Х), а на коробку, согласно третьему закону Ньютона, сила той же величины, но имеющая противоположное направление. Тогда уравнения движения груза и коробки будут такими:

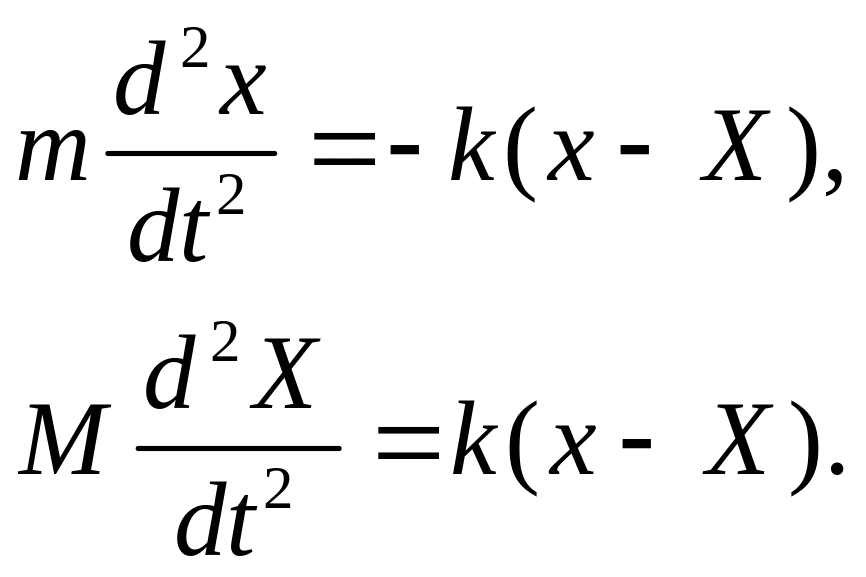(1).

Если разделить первое из этих уравнений на т, а второе – на М, и вычесть из первого уравнения второе, то придём к уравнению:

,

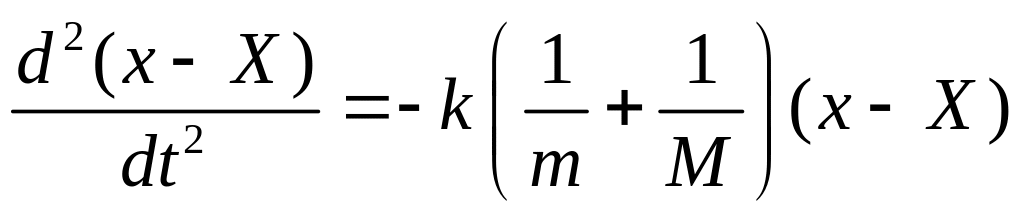которое является уравнением гармонических колебаний для у = х – Х :

.

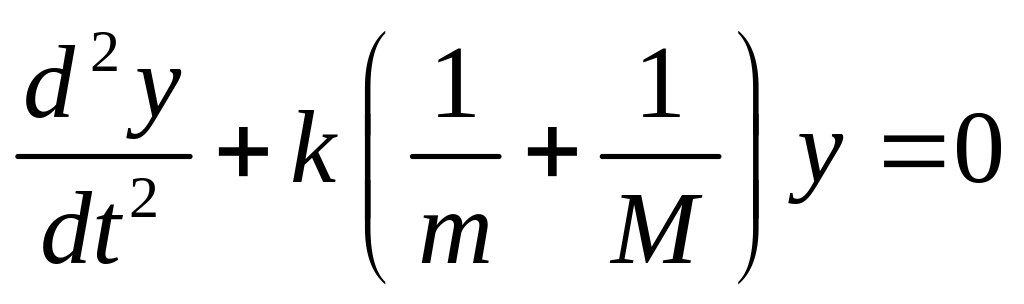Квадрат частоты колебаний есть коэффициент перед у, откуда сама частота:

.

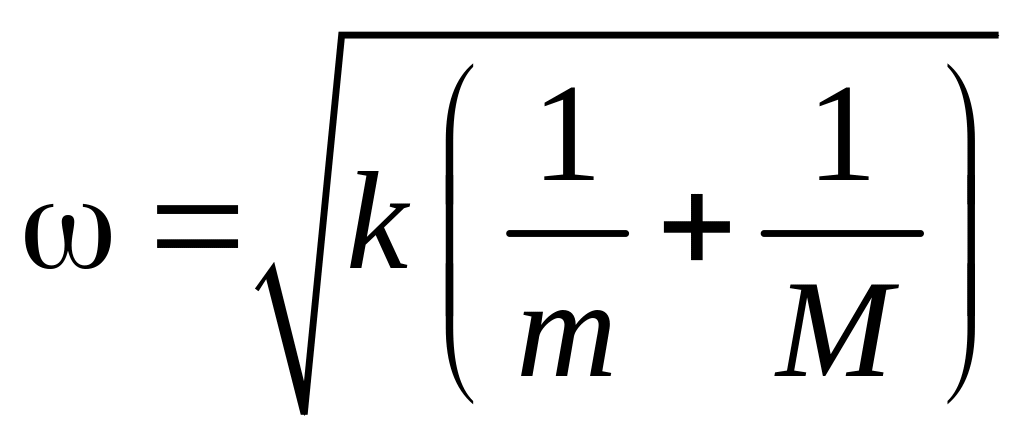Если сложить оба уравнения системы (1), то получим:

.

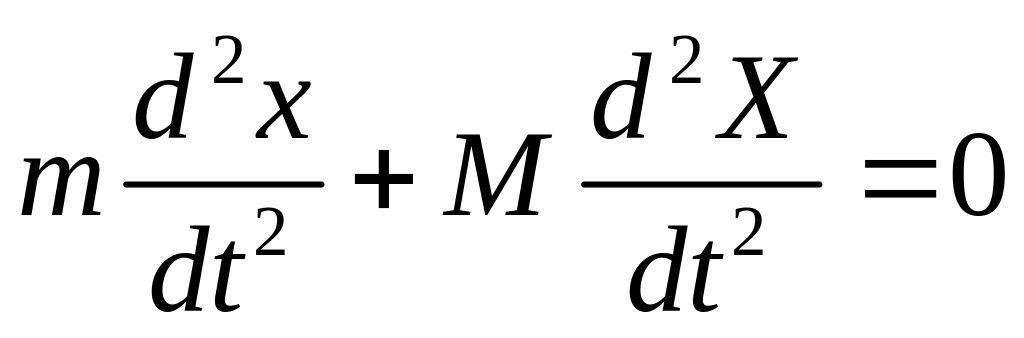Это уравнение можно записать как:

,

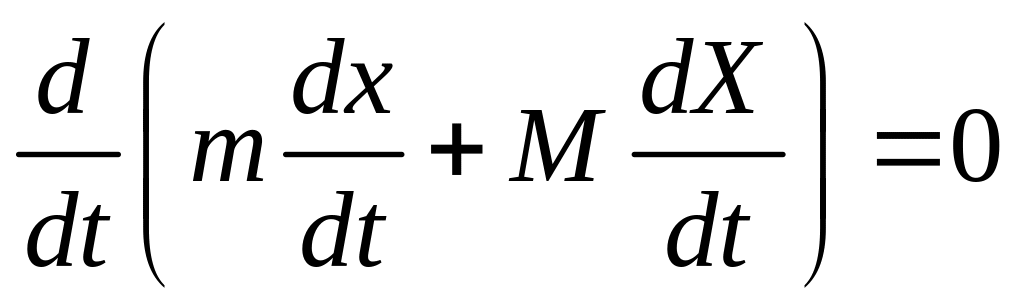или:

.

Полученное уравнение представляет собой закон сохранения импульса: импульс груза и коробки остаётся постоянным.

Задача 10

По вогнутой цилиндрической поверхности радиуса R катается цилиндр радиуса r. Найти частоту малых колебаний цилиндра, если он движется без проскальзывания.

Решение

Рис. 1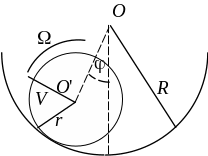

Поскольку движение происходит без проскальзывания, то сила трения работы не совершает (см. обсуждение этого факта в задаче 10 раздела 7). Поэтому энергия цилиндра сохраняется. Вычислим ее. Рассмотрим движение цилиндра в произвольный момент времени, считая, что скорость его центра инерции равна V, а угол между вертикалью и радиусом-вектором, проведенным из О в О' (см. рис. 1) равен . В этот момент потенциальная энергия цилиндра есть:

U = – mg(R–r)cos

Здесь мы отсчитываем высоту, на которой находится центр масс цилиндра от точки О. Кинетическая энергия цилиндра в этот же момент времени:

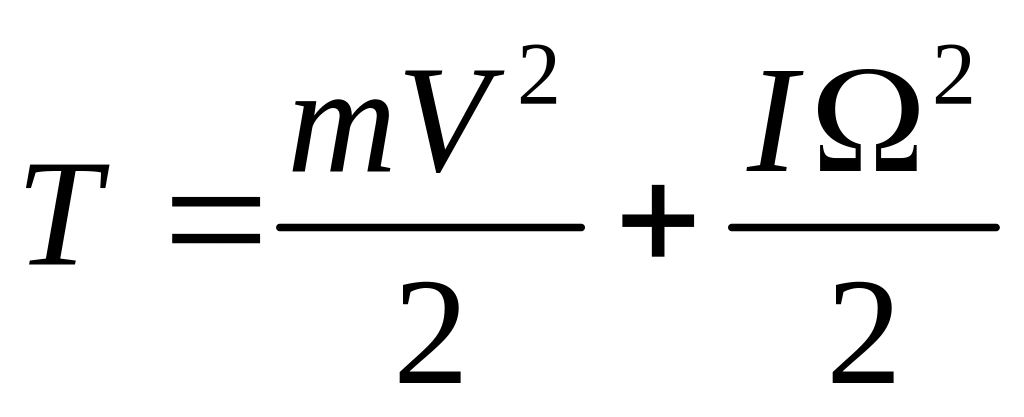
где т – масса цилиндра, I – момент инерции цилиндра относительно его оси,  – угловая скорость вращения цилиндра. Свяжем V и , учитывая, что цилиндр катится без проскальзывания. Скорость можно записать как r, так как мгновенная ось вращения цилиндра совпадает с линией касания цилиндра с поверхностью, по которой он движется. Итак:

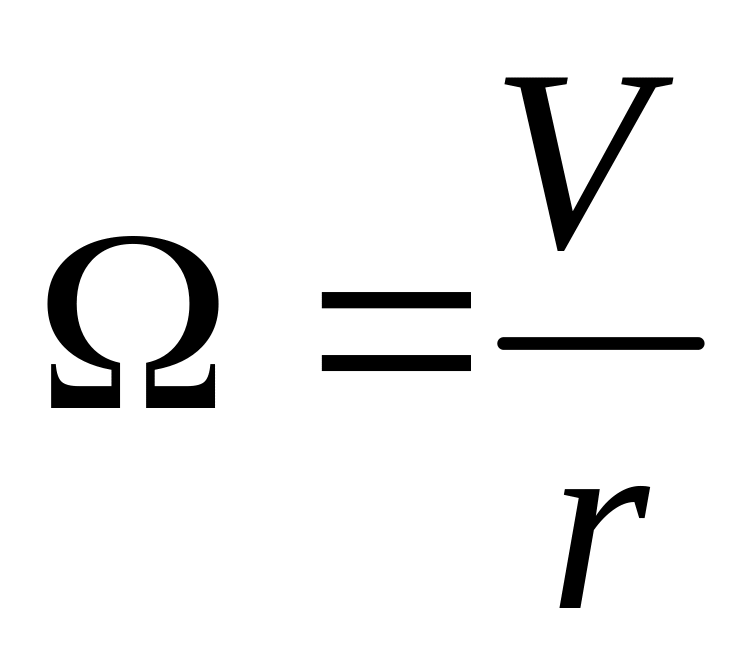
С другой стороны, можно записать:

так как центр инерции цилиндра движется по окружности радиуса R–r с центром в точке O. Выразив V и  через d/dt, окончательно получаем для энергии цилиндра:

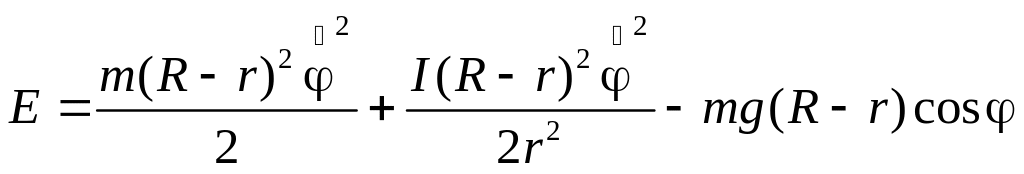
Дифференцируя (5) по времени, получаем:

.

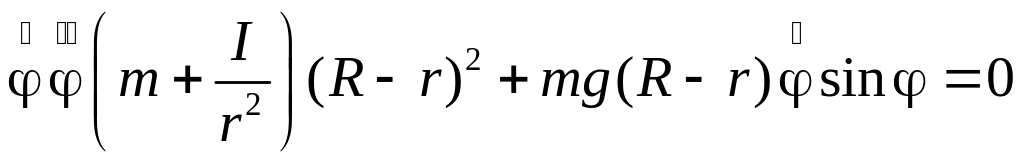После сокращений получим:

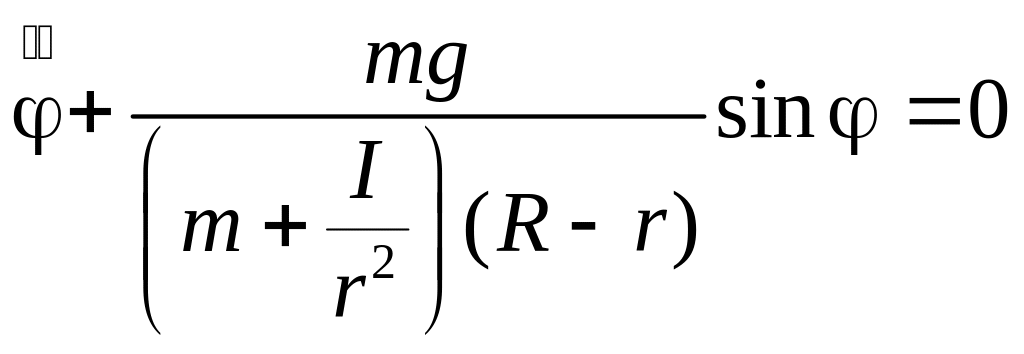
Считая колебания малыми, т.е. ||<<1 можем полагать sin =  и тогда приходим к уравнению гармонических колебаний:

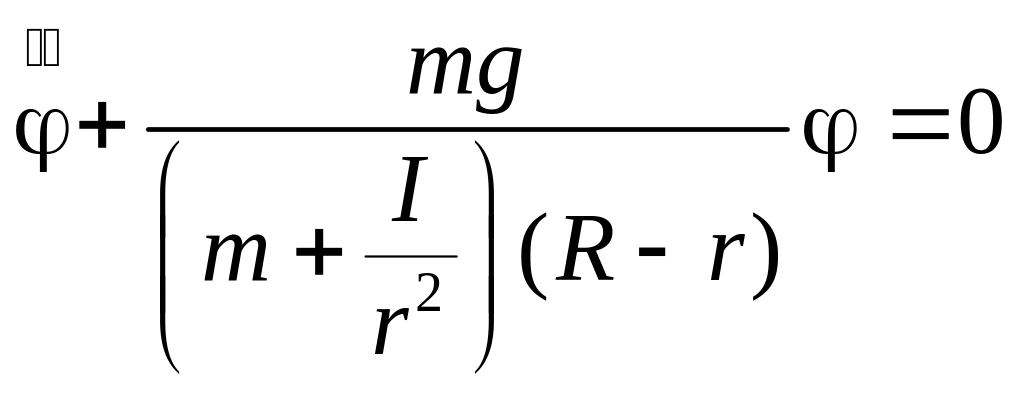
Коэффициент при  есть квадрат частоты этих колебаний, соответственно, частота равна:

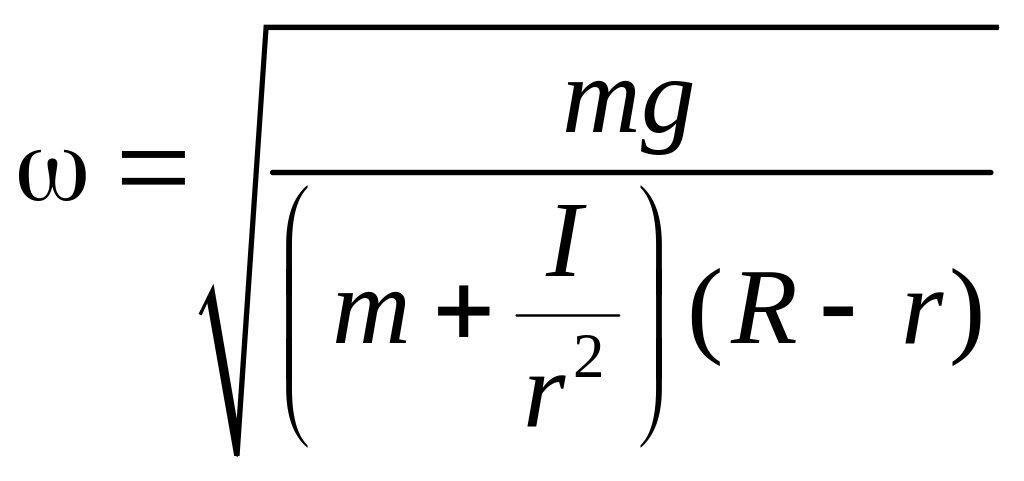
Учитывая, что I = тr²/2, окончательно находим:

.

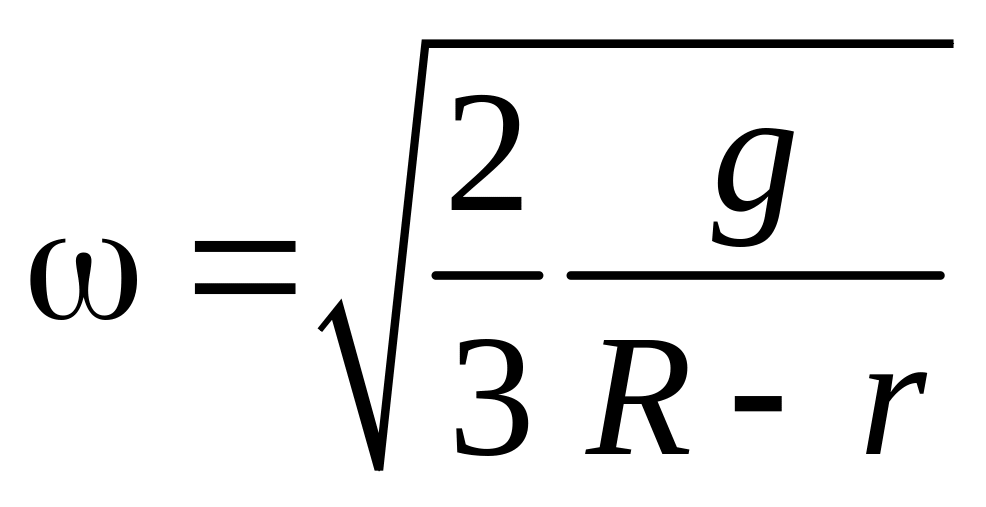1 Здесь выбор систем отсчёта пока ограничен лишь такими системами отсчёта, которые не вращаются одна относительно другой.

1 Фактически мы доказали известную теорему о том, что медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 1:2

1 Произведение Fdt называют импульсом силы. Таким образом, изменение импульса тела равно импульсу силы, действующей на тело

1 Любители строгих выводов могут убедиться, что и в самом общем случае результат тот же: