Решение

В ходе решения задачи 6 раздела 8 мы получили выражение для потенциальной энергии шарика в системе отсчета, вращающейся вместе с шариком:

.

Рис. 1

Потенциальная энергия U, как мы видели, имеет минимум, положение которого зависит от величины угловой скорости . Если шарик получил, небольшой толчок, так что угол  получил приращение  (||<<1), то шарик начнет колебаться вблизи своего равновесного положения. Напомним, что мы рассматриваем движение шарика в неинерциальной системе отсчета, вращающейся вместе с шариком вокруг вертикали. В неподвижной системе отсчета движение шарика будет суммой равномерного вращения вокруг вертикальной оси и колебаний в вертикальной плоскости. Чтобы найти частоту этих малых колебаний, разложим по формуле Тейлора потенциальную энергию шарика по степеням  до величин второго порядка включительно. Такое разложение, как известно, имеет вид:

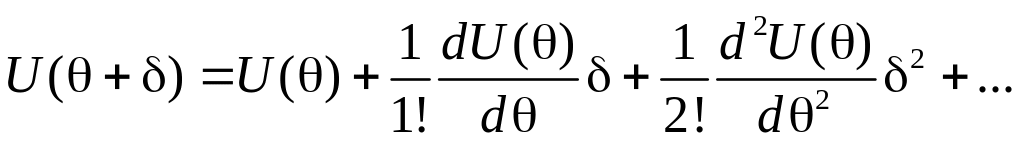
В нашем случае первая производная от U равна нулю, т.к. в положении равновесия U() имеет минимум, поэтому разложение начинается с члена второго порядка по :

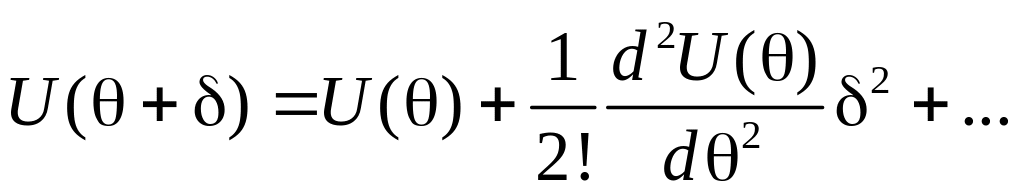
Вычисляя вторую производную от U, получим:

.

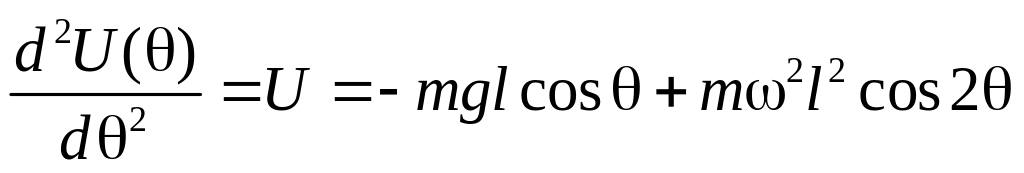Нам нужно найти вторую производную в положении равновесия, которое зависит от величины угловой скорости:

.

В первом случае, когда ²< g/l получаем:

(1),

а во втором, когда ² > g/l:

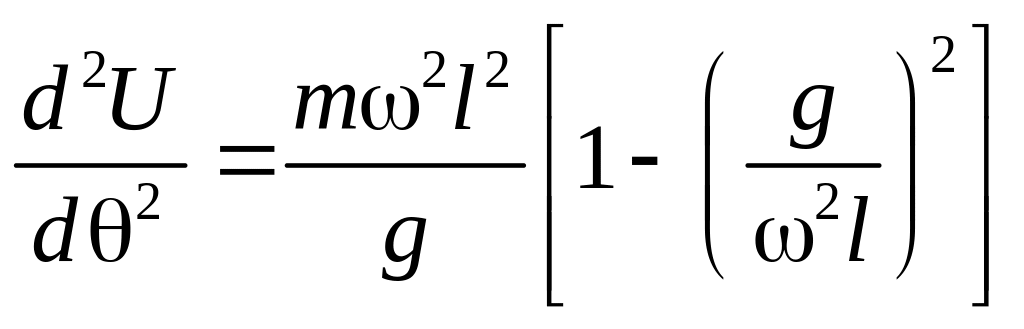(2).

С учётом полученных выражений запишем потенциальную энергию в окрестности положения равновесия:

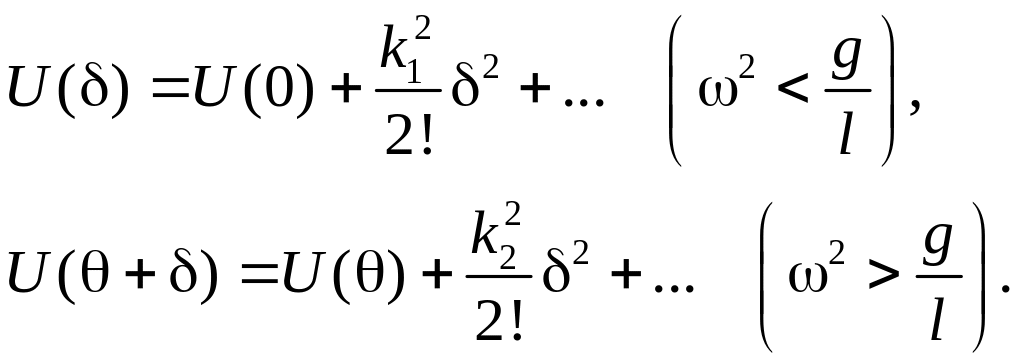
Здесь k₁² и k₂² – правые части соотношений (1) и (2).

При колебаниях шарик движется по дуге окружности радиуса l (см. рис.1), поэтому его скорость v = ld/dt. Кинетическая энергия шарика тогда запишется следующим образом:

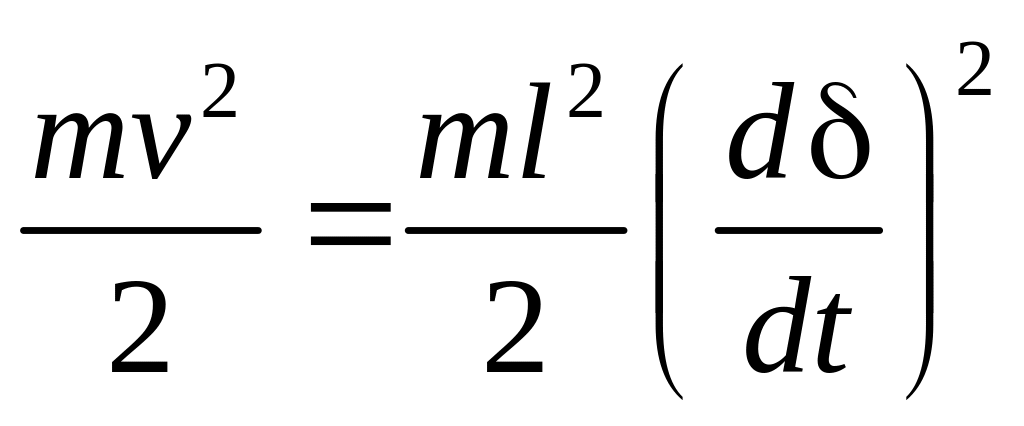(3).

Поскольку энергия шарика Е остается постоянной, то dE/dt = 0, откуда, с помощью (1) – (3) получаем следующие уравнения колебаний шарика:

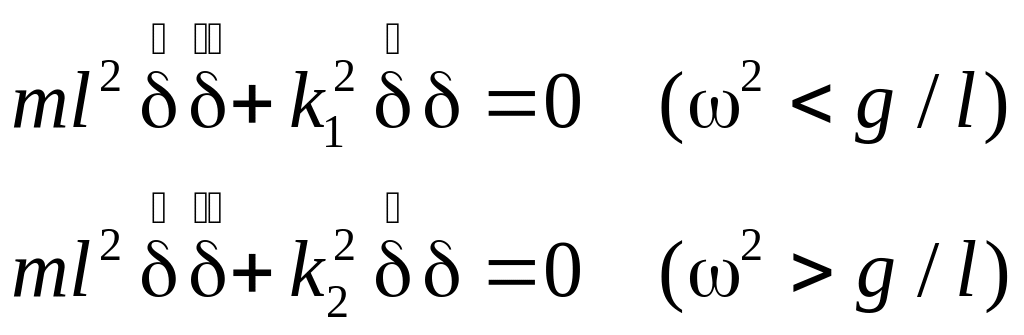
Поделив их на ml², придем к уравнениям гармонических колебаний:

,

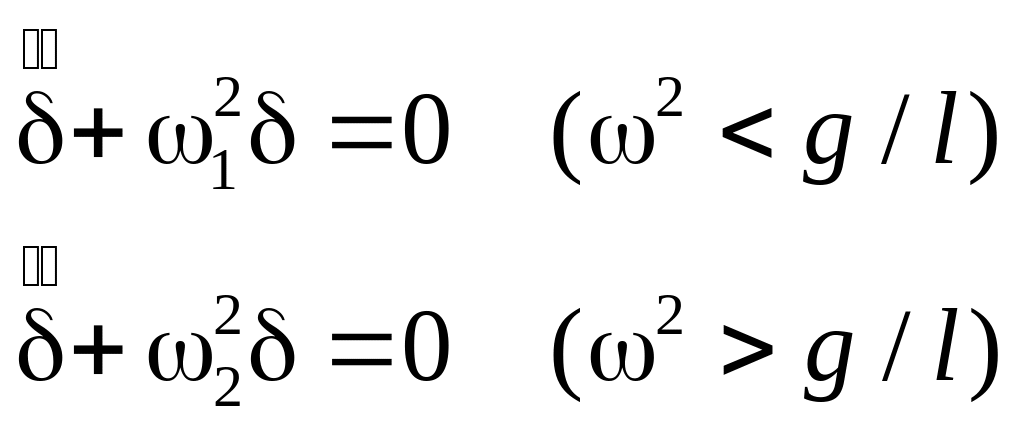где частоты колебаний ₁ и ₂ согласно (1) – (2):

Задача 7

В одном из фантастических проектов предлагалось построить железнодорожный тоннель для скоростных поездов, которые бы двигались под действием одной только силы тяжести. Для этого тоннель, идущий под землёй должен быть прямым. Найдите время движения поезда от одного конца тоннеля до другого, пренебрегая всеми силами сопротивления.

Решение

Рис. 1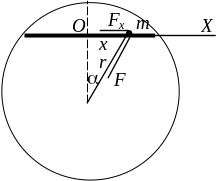

В задаче 8 раздела 2 была найдена сила тяготения, действующая на тело массы т, находящееся внутри Земли на расстоянии r от её центра:

.

Выберем начало координат в середине тоннеля и проведём ось координат ОХ вдоль тоннеля. Пусть поезд находится на расстоянии х от середины тоннеля. Тогда проекция силы тяжести на направление оси ОХ равна:

.

Как видим, эта сила пропорциональна расстоянию х между телом и центром тоннеля и направлена к центру тоннеля, т.е. к положению равновесия. Но такая сила приводит к гармоническим колебаниям тела с частотой:

.

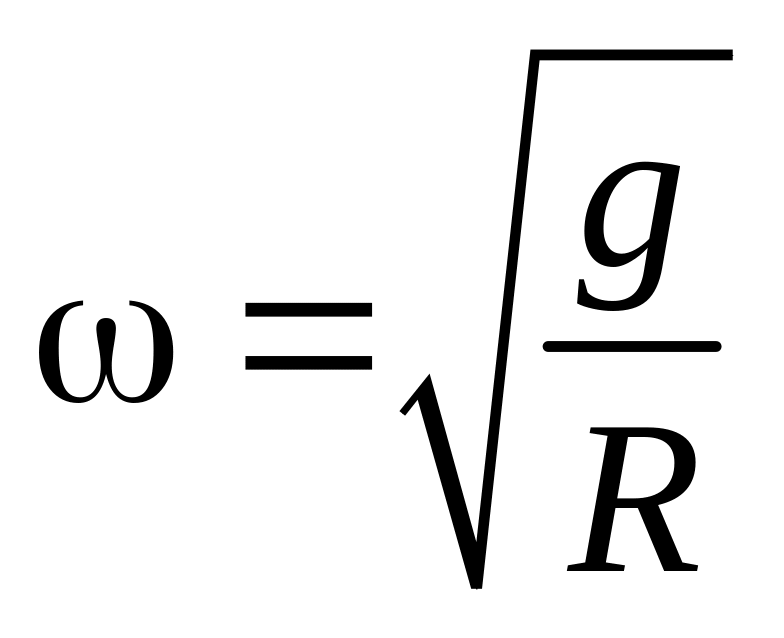Время движения поезда от одного кон­ца тоннеля до другого равно половине периода колебаний:

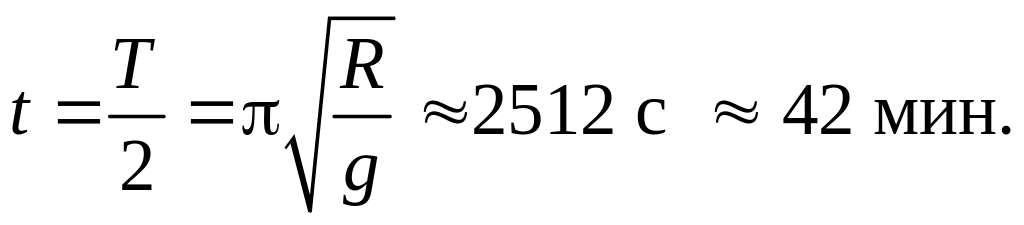
Задача 8

Оценить время соударения футбольного мяча со стенкой при слабом ударе.