
Ми10 крив и пов
.pdfМинистерство образования и науки Российской Федерации Южно-Уральский государственный университет Кафедра дифференциальных и стохастических уравнений
517.3 (07) П207
А.А. Патрушев, А.А. Эбель
КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ
Учебное пособие
Челябинск Издательский центр ЮУрГУ 2013
УДК 517.3 (075.8) П207
Одобрено научно-методическим советом по математике и механике
Южно-Уральского государственного университета
Рецензенты:
профессор, доктор физ.-мат. наук М.М. Кипнис, профессор, доктор технических наук П.П. Переверзев
Патрушев, А.А. Криволинейные и поверхностные интегралы, элементы тории поля: учебное пособие для самостоятельной работы студентов / А.А. Патрушев, А.А. Эбель. – Челябинск: Издательский центр ЮУрГУ, 2013. – 116 с.
Учебное пособие предназначено для самостоятельного изучения раздела «Криволинейные и поверхностные интегралы, элементы тории поля» из курса математического анализа студентами технических специальностей. Изложение учебного материала иллюстрируется примерами. В пособие включены задачи для самостоятельного решения, снабжённые ответами.
УДК |
517.3 (075.8) |
Издательский центр ЮУрГУ, 2013
2
Введение
При изучении физики, механики и при решении разнообразных инженерных задач часто возникает необходимость наряду с интегралами от действительной функции одного переменного рассматривать интегралы от функций многих переменных по кривым и поверхностям. Такие интегралы играют важную роль при исследовании скалярных и векторных полей, задаваемых в пространстве действительными и векторными функциями векторного аргумента, составляющими предмет изучения теории поля и векторного анализа.
Настоящее пособие содержит краткое изложение основного материала по криволинейным и поверхностным интегралам, входящего в курс математического анализа для студентов технических специальностей. Особое внимание уделено векторным и скалярным полям. В пособии рассмотрено множество примеров и предложены задачи для самостоятельного решения по каждому разделу изучаемого материала. Все задачи снабжены ответами; приведен список литературы.
Пособие может быть использовано как сборник задач, а также в качестве руководства к самостоятельному изучению раздела математического анализа: «Криволинейные и поверхностные интегралы, элементы теории поля.
3
Кривые |
1. Криволинейные интегралы |
|||||
|
|
|
|
|||
|
Непрерывная кривая на плоскости есть геометрическое место точек, |
|||||
удовлетворяющих одному из аналитических соотношений: |
||||||
а) |
y = f (x) – явное задание кривой; |
|
||||
б) |
F(x, y) = 0 – неявное задание кривой; |
|||||
в) |
x =ϕ(t); |
– параметрическое задание кривой. |
||||
|
=ψ(t), |
|||||
|
y |
|
|
|
|
|
Здесь мы предполагаем, что функции, определяющие кривую, являются |
||||||
непрерывными. |
x =ϕ |
(t); |
|
|||
|
Непрерывная кривая |
t (a,b) называется гладкой, если |
||||
|
|
(t), |
||||
|
|
|
|
y =ψ |
|
|
функции ϕ(t) и ψ(t) имеют непрерывную производную на (a,b) и |
||||||
выполняется неравенство ϕ' (t)2 |
+ψ ' (t)2 ≠ 0, t (a,b). |
|||||
|
Непрерывная кривая |
F(x, y) = 0 называется гладкой в окрестности |
||||
точки M (x0 , y0 ) , если функция F(x, y) имеет непрерывные частные производные в окрестности точки M (x0 , y0 ) и Fx' (x0 , y0 )2 +Fy' (x0 , y0 )2 ≠ 0.
Точка M (x0 , y0 ) в этом случае |
называется обыкновенной точкой кривой. |
Непрерывная кривая y = |
f (x) , x (a,b) называется гладкой, если |
функция f (x) имеет непрерывную производную на этом интервале.
Очевидно, кривую, заданную явно, можно записать в параметрическом виде
|
x = x; |
, |
x (a,b) . |
|
|
|
f (x), |
||
y = |
|
|
||
То же самое можно утверждать и о неявно заданной кривой в окрестности обыкновенной точки. Поэтому, в основном, мы будем рассматривать гладкие кривые, заданные параметрически.
Непрерывная кривая, составленная из конечного числа гладких кривых,
называется кусочно-гладкой. Простейшим примером кусочно-гладкой кривой может служить ломаная линия с конечным числом звеньев.
На каждой гладкой кривой можно выбрать определенное положительное направление, а именно то, которое соответствует возрастанию параметра t .
Непрерывная кривая x =ϕ(t); |
, t [a,b] называется замкнутой, если |
y =ψ(t), |
|
(ϕ(a),ψ(a)) = (ϕ(b),ψ(b)) . |
|
Непрерывная кривая, не пересекающая себя и не касающаяся себя, называется простой кривой.
Формулы отсутствия самопересечений и самокасаний записываются так:
4
ϕ(t1 ) −ϕ(t2 ) +ψ(t1 ) −ψ(t2 ) ≠ 0 при t1 −t2 ≠ 0.
Наиболее часто встречающиеся в задачах кривые на плоскости.
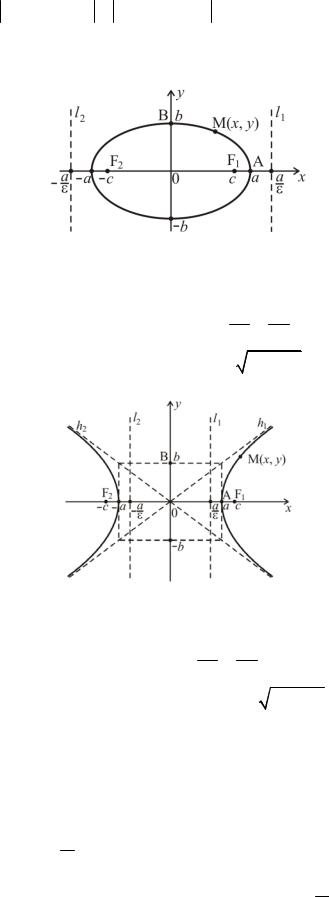
Кривые второго порядка 1.Эллипс
1. Сумма расстояний от каждой точки эллипса до его фокусов есть величина постоянная, равная 2а.
2. Каноническое уравнение эллипса (а > b): x2 + y2 =1. a2 b2
3. Фокусы эллипса: F (c;0), F (−c;0) , где c = a2 |
−b2 . |
|
1 |
2 |
|
2. Гипербола
1. Модуль разности расстояний от каждой точки гиперболы до ее фокусов есть величина постоянная, равная 2а.
2. Каноническое уравнение гиперболы: x2 − y2 =1. a2 b2
3. Фокусы гиперболы: F (c;0), F (−c;0) , где c = a2 |
+b2 . |
|
1 |
2 |
|
3. Парабола
1.Произвольная точка М (х; у) параболы равноудалена от фокуса и директрисы параболы: ρ(М; F) = ρ(М; l)
2.Каноническое уравнение параболы: y2 = 2 px.
3.Фокус параболы: F( 2p ;0)
4.Директриса параболы – прямая l с уравнением: x = − 2p .
5
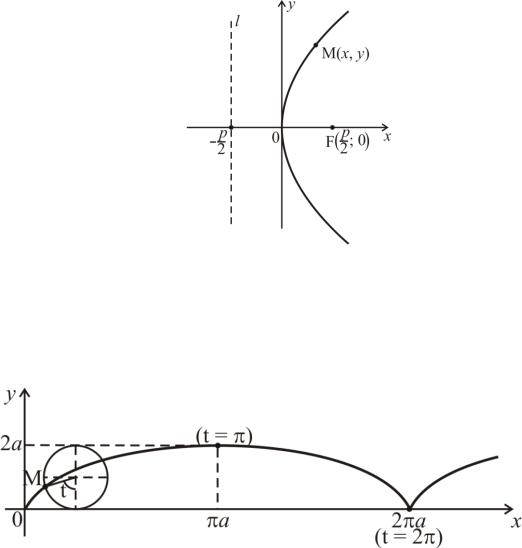
Кривые, заданные параметрически.
Циклоида:
x = a(1 −sin t); |
t (−∞;∞). |
|
|
−cost), |
|
y = a(1 |
|
|
Характеристическое свойство: кривая является траекторией точки М окружности радиуса а, которая катится без скольжения по оси 0х (в начальный момент времени точка находится в начале координат).
|
3 |
|
|
|
Астроида: x = acos |
t; |
t [0;2π) (или x2/3 + y2/3 = a2/3 ). |
||
|
||||
y = asin3 t, |
|
|||
Характеристическое свойство: всякая точка этой кривой есть основание перпендикуляра РМ к отрезку постоянной длины а, движущемуся так, что концы его все время находятся на координатных осях (точка Р – точка пересечения прямых, проходящих через концы отрезка параллельно координатным осям).
6
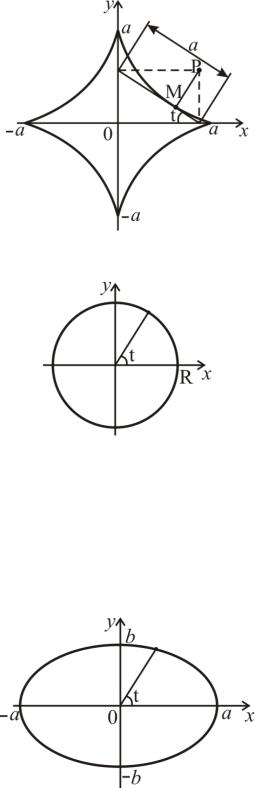
Окружность радиуса R с центром в начале координат:
x = Rcost; |
t [0;2π) (или x2 + y2 = R2 ). |
|
|
y = Rsin t, |
|
Эллипс с полуосями а и b с центром в начале координат:
x = acost; |
t [0;2π) (или |
x |
2 |
+ |
y |
2 |
=1). |
|
|||||||
|
|
|
|||||
a |
|
b2 |
|||||
y = bsin t, |
|
2 |
|
|
|||
В общем случае, для построения «незнакомой» кривой, заданной параметрически, нужно попробовать исключить параметр t из параметрических уравнений, получив, там самым, уравнение вида
F(х, у) = 0 (или f(х) = у).
7
Пример 1.1. Построить линию, заданную параметрически:
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x =1 + |
|
|
; |
t (− |
π |
; |
π |
|
). |
|
|
|
|
|
|
|
|||
|
cost |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|||||||
|
|
y = tgt |
−1, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
t целесообразно |
|
|
|
|
|||||||||||||
Решение. Для исключения параметра |
использовать |
|||||||||||||||||||
известную из тригонометрии формулу: tg |
2t +1 = |
|
|
1 |
|
|
|
. Выражая из второго |
||||||||||||
cos2 t |
||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
1 |
|
x −1 |
|
|||||||
уравнения |
tgt : tgt = y +1, а из первого уравнения |
|
|
: |
= |
,−и |
||||||||||||||
|
|
cost |
cost |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
||||
подставляя |
найденные выражения |
в указанную |
|
|
тригонометрическую |
|||||||||||||||
формулу, получаем уравнение гиперболы |
(x −1)2 |
− |
( y +1)2 |
|
|
|
|
|||||||||||||
9 |
|
|
|
|
|
1 |
=1 с центром в |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
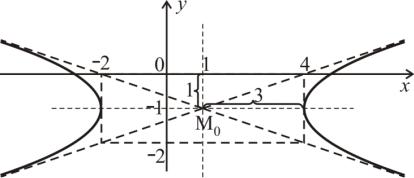
точке М0(1; −1), с осями, параллельными осям координат, с действительной осью, параллельной оси 0х. Гипербола изображена на рис. 1.1:
Рис. 1.1.
В некоторых случаях исключение параметра не приводит к упрощению «узнавания» и построения кривых. Тогда для построения кривой придают различные значения параметру t и для каждого значения находят соответствующие значения х и у. Затем, в декартовой системе координат по точкам (х; у) строят кривую, отображающую зависимость у(х).
Пример 1.2. Построить кривую, заданную параметрически:
x =1 +t2
y = t3 − 4t.
Решение. Исключение параметра t из заданных параметрических уравнений кривой не приводит к уравнению знакомой кривой. Поэтому, для начала, находим точки пересечения данной кривой с координатными осями:
1) x = 0 невозможно, следовательно, пересечений с осью 0у нет;
8
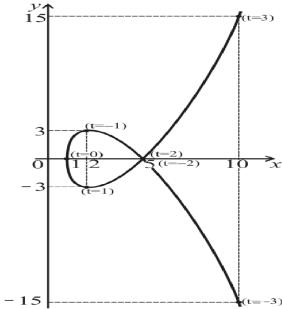
t1 = 0 (x =1);
2)y = 0 : t2 = 2 (x = 5);
t3 = −2 (x = 5).
Рис. 1.2.
Очевидно, что в точке (х = 5, у = 0) кривая пересекает сама себя, так как она проходит через эту точку при двух различных значениях параметра t (t2 = 2 и t2 = −2 ). Далее, придавая параметру t некоторые значения,
t |
х |
у |
|
|
|
−3 |
10 |
−15 |
|
|
|
−2 |
5 |
0 |
|
|
|
−1 |
2 |
3 |
0 |
1 |
0 |
|
|
|
1 |
2 |
−3 |
2 |
5 |
0 |
3 |
10 |
15 |
находим соответствующие значения х и у и по точкам (х; у) схематично строим кривую (с петлей) в декартовых координатах (рис. 1.2).
Кривые, заданные в полярных координатах r = r(ϕ)
Замечание. При рассмотрении кривых полюс полярной системы координат помещен в точку (0;0) декартовой системы координат, полярная ось совмещена с положительной полуосью абсцисс.
9
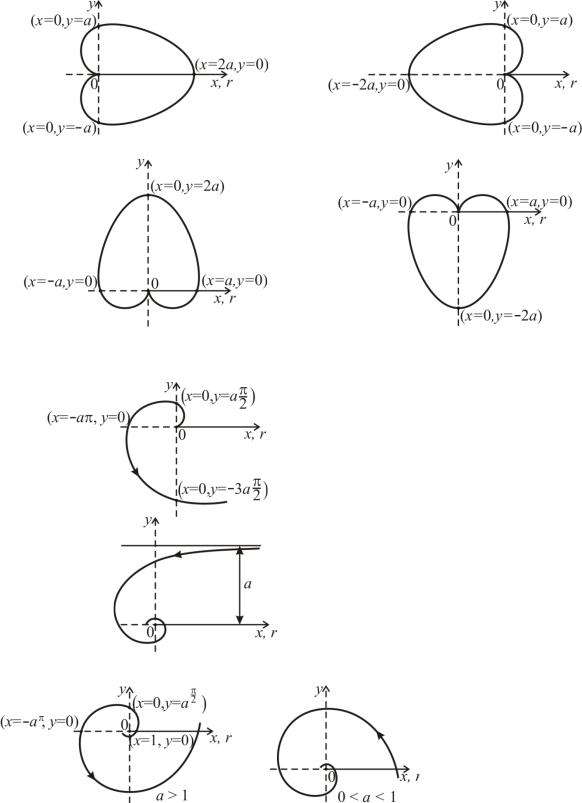
Кардиоиды
r = а(1 + cosϕ); |
r = а(1 − cosϕ); |
r = а(1 + sinϕ); |
r = а(1 − sinϕ). |
Cпирали
спираль Архимеда: r = а·ϕ;
гиперболическая спираль:
r = а/ϕ;
логарифмическая
спираль: r = аϕ.
Стрелками на рисунках указано направление, соответствующее возрастанию ϕ.
10
