
Ми10 крив и пов
.pdf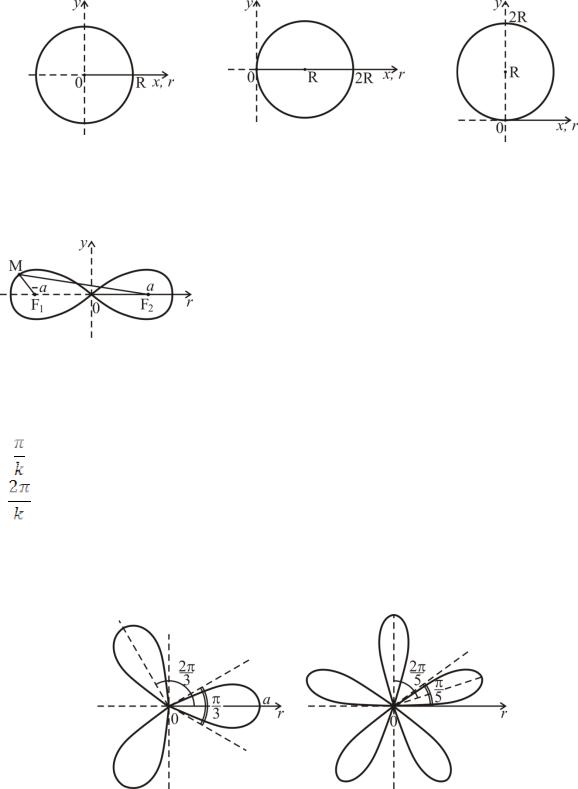
Окружности
r = R |
r = 2Rcosϕ |
r = 2Rsinϕ |
(или х2 + у2 = R2); |
(или (х − R)2 + у2 = R2); |
(или х2 + (у − R)2 = |
R2).
Лемниската Бернулли
r2 = 2а2cos2ϕ (или (х2 + у2)2 = 2а2(х2 − у2)).
Характеристическое свойство: |F1M|·|F2M| = а2, где F1(−а; 0), F2(а; 0).
k-лепестковые розы
r = аcoskϕ, r = аsinkϕ, k N, а ≥ 0;
k − количество лепестков розы; a − наибольшая длина лепестка;
− «ширина» одного лепестка (соответствует длине интервала
изменения угла ϕ для одного лепестка, находится их условия
coskϕ ≥ 0 или sinkϕ ≥ 0);
− угол между осями симметрии соседних лепестков (соответствует периоду соответствующей тригонометрической функции coskϕ
или sinkϕ).
r = acos3ϕ r = asin 5ϕ
Следует отметить, что розы вида r = аcoskϕ симметричны относительно полярной оси (в силу четности косинуса), а розы r = аsinkϕ симметричны относительно вертикальной оси,
11
проходящей через полюс (уравнение этой оси в полярных кооординатах ϕ = π/2). Если дано уравнение кривой в полярных координатах, не относящееся к вышеперечисленным типам, поступают следующим образом.
Сначала нужно попробовать перевести уравнение кривой в декартовые координаты, что иногда существенно облегчает задачу (так, например, из уравнения r = а/sinϕ, при переходе к декартовым координатам, получаем уравнение прямой у = а).
Если переход к декартовым координатам не дает желаемых результатов, то заданную кривую строят «по точкам», т.е. находят значения r(ϕ), придавая ϕ различные, целесообразные для данной конкретной задачи, значения. Здесь необходимо помнить, что r − полярный радиус, по определению, должне быть неотрицателен, то есть первое условие при выборе значений ϕ: r(ϕ) ≥ 0. Далее, для упрощения построений, нужно учитывать период тригонометрических функций, входящих в уравнение кривой, а так же симметрию кривой (см. выше).
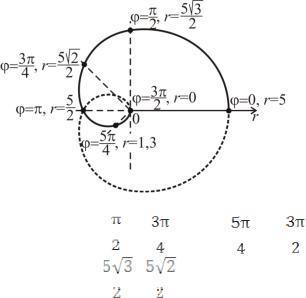
Пример 1.3. Построить кривую r = 5cos ϕ3
Решение. 1. Находим значения полярного угла ϕ, при которых значения r(ϕ) неотрицательны: r(ϕ) ≥ 0, то есть
5cos |
ϕ |
≥ 0 − |
π |
+ 2πn≤ |
ϕ |
≤ |
π |
+ 2πn или |
|||
|
|
3 |
|
2 |
|
|
|
3 |
|
2 |
|
− |
3π |
+ 6πn ≤ϕ ≤ |
3π |
+ 6πn, n |
Z. |
||||||
|
2 |
2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
||
ϕ |
|
0 |
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
r = 5cos |
ϕ |
5 |
|
|
|
|
|
|
|
|
|
|
2, |
1,3 |
|
0 |
|
||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
12

2.В силу периодичности функции r = 5cosϕ/3, будет достаточно найти зависимость r от ϕ для одного промежутка изменения ϕ (при n = 0).
3.Так как косинус – функция четная, то можно построить кривую для ϕ ≥ 0 , а для ϕ < 0 она будет симметрична относительно полярной оси.
4.Из вышесказанного следует, что целесообразно рассматривать значения
ϕ[0; 3π/2]. Находя соответствующие значения r(ϕ), строим кривую.
Пример 1.4. Построить кривую r = 2 + sin4ϕ.
Решение. 1. Условие r(ϕ) ≥ 0, очевидно, выполняется для всех



 .
.
2.Так как sin4ϕ − функция периодическая с периодом Т = π/2, то целесообразными значениями полярного угла ϕ являются значения из промежутка, длина которого равна периоду Т = π/2, например, значения
ϕ[−π/4; π/4]. Для упрощения вычислений среди указанных значений ϕ выбираем те, для которых значения sin4ϕ являются табличными (см. 1.12). Результаты вычислений сводим в таблицу и строим соответствующую часть кривой.
3.В силу периодичности функции sin4ϕ (а, следовательно, и функции r = 2 + sin 4ϕ), переносим построенную часть кривой на очередной сектор
изменения ϕ, длина которого равна Т = π/2: на сектор ϕ [π/4; 3π/4]. Повторяя подобную процедуру еще 2 раза, получаем
искомую кривую, состоящую из четырех одинаковых частей.
ϕ |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4ϕ |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
sin4ϕ |
0 |
|
−1 |
|
−0,5 |
|
0 |
0,5 |
|
|
1 |
|
0 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
r=2+sin4ϕ |
2 |
|
1 |
|
1,5 |
|
2 |
2,5 |
|
|
3 |
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналогично вводится понятие кривой в пространстве. Непрерывная кривая в пространстве есть геометрическое место точек, удовлетворяющих одному из аналитических соотношений:
y = f (x); |
– явное задание кривой; |
а) |
|
z = g(x), |
|
13
|
F(x, y, z) = 0; |
– неявное задание кривой (пересечение двух |
|
б) |
0, |
||
|
G(x, y, z) = |
|
|
поверхностей); |
|
|
|
|
x =ϕ(t); |
|
|
в) |
|
|
|
y =ψ(t); – параметрическое задание кривой. |
|||
|
|
|
|
|
z = χ(t), |
|
|
Здесь мы предполагаем, что функции, определяющие кривую, являются непрерывными. Аналогичным образом, как и для кривых на плоскости, определяется понятие гладкой и кусочно-гладкой кривой.
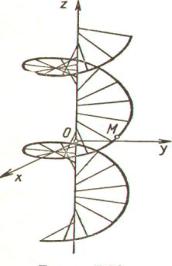
Наиболее часто встречающиеся в задачах кривые в пространстве 1. Винтовая линия
x = acosωt; |
|
|
|
Параметрические уравнения линии: y = asinωt; |
|
|
z =νt, |
|
|
Рис. 1.3.
Винтовая линия - линия, описываемая точкой M, которая вращается с постоянной угловой скоростью ω вокруг неподвижной оси (Oz) и одновременно перемещается поступательно с постоянной скоростью ν вдоль этой оси (рис. 1.3).
14

2. Линия Вивиани
x2 + y2 + z2 = a2 ;
Неявные уравнения линии:
x2 + y2 − ax = 0,
Рис. 1.4.
Линия Вивиани - линия пересечения сферы радиуса a с круглой цилиндрической поверхностью, диаметр которой равен радиусу сферы и одна из образующих проходит через центр сферы (рис. 1.4).
3. Коническая винтовая линия
x = at cost; |
|
|
|
Параметрические уравнения линии: y = at sin t; |
|
|
z = bt, |
|
|
Рис. 1.5.
15
Коническая винтовая линия – линия, описываемая точкой M, которая движется по прямой OL с постоянной скоростью, а прямая OL, не перпендикулярная к оси Oz, равномерно вращается вокруг нее с постоянной угловой скоростью (см. рис. 1.5)
Кривая называется спрямляемой кривой, если она имеет конечную длину. Как известно, кусочно-гладкая кривая спрямляема. Всюду, в дальнейшем (если не оговорено противное) под терминами «кривая», «путь», «контур», «линия» мы будем понимать кусочно-гладкую кривую.
На гладкой кривой в качестве параметра t мы можем взять длину дуги s , отсчитываемую от некоторой фиксированной точки кривой и снабженную определенным знаком в зависимости от направления отсчета. Такой параметр обычно называют естественным или натуральным
параметром кривой. |
|
|
|
|
Как известно из |
раздела определенного интеграла по отрезку, если |
|||
гладкая кривая L на плоскости задана параметрически: |
x =ϕ |
(t); |
t [α;t], |
|
|
(t), |
|||
|
|
y =ψ |
|
|
то длина кривой |
s(t) определяется равенством |
s(t) = ∫t |
x'2 + y'2 dt . |
|
|
|
α |
|
|
Следовательно, на основании теоремы Барроу, дифференциал длины дуги
t |
' |
ds = ∫ |
x'2 + y'2 dt dt = x'2 + y'2 dt. |
α |
t |
Аналогично, имеем:ds = |
1 + f '2 (x)dx, если кривая задана явно y = f (x); |
ds = r2 + r'2 dϕ, если |
кривая задана в полярной системе координат |
r = r(ϕ) . |
|
Так же можно показать, что дифференциал длины дуги в пространстве задается формулой: ds = x'2 + y'2 + z'2 dt, если кривая задана
x =ϕ(t);
параметрически y =ψ(t);
z = χ(t).
1.1Криволинейный интеграл первого рода
1.1.1Понятие криволинейного интеграла первого рода
Пусть в трехмерном пространстве с системой координат Охуz имеется кривая которой задана действительная функция
прямоугольной декартовой AB (рис. 1.2.1), в точках f (M ) = f (x, y, z). Выберем
разбиение |
T ={A0 , A1 ,..., An} кривой AB с |
точками деления |
A0 = A, A1 , |
..., An = B . Длины элементарных дугAi−1 Ai |
обозначим через ∆si , |
16

а максимальную из этих длин – через λ = λ(T) . Возьмем на каждой дуге Ai−1 Ai по точке Mi (xi , yi , zi ) , и вычислим значение функции f (Mi ) = f (xi , yi , zi ) в этой точке.
Рис. 1.2.1.
Отметим, что подобное разбиение можно построить и в случае замкнутой кривой, если за точку A0 , совпадающую в этом случае с An , взять любую
точку кривой AB , а остальные точки Ai ,i =1,..., n −1, расположить в
соответствии с выбранным направлением на этой замкнутой кривой. Составим сумму вида
n |
|
∑ f (xi , yi , zi )∆si . |
(1.1) |
i=1
которую называют интегральной суммой функции f (x, y, z) вдоль кривой АВ. Если существует предел интегральных сумм (1.1) при λ(T) → 0 ,
который не зависит ни от выбора разбиения кривой AB , ни от выбора точек Mi на элементарных дугах Ai−1 Ai , то такой предел называют
криволинейным интегралом первого рода вдоль пространственной кривой AB. Итак,
|
n |
|
|
limλ→0 |
∑ f (xi , yi , zi )∆si = |
∫ f (x, y, z)ds. |
(1.2) |
|
i=1 |
AB |
|
Рис. 1.2.2.
В частности, когда кривая задана на плоскости Oxy, криволинейным интегралом первого рода вдоль плоской кривой AB называется
17
n |
∫ f (x, y)ds, который не |
|
|
limλ→0 ∑ f (xi , yi )∆si = |
зависит ни от выбора |
||
i=1 |
AB |
Mi |
|
разбиения кривой |
AB , ни от выбора точек |
на элементарных дугах |
|
Ai−1 Ai (рис.1.2.2). |
|
|
|
Если кривая АВ спрямляема, можно ввести |
натуральный параметр s |
||
этой кривой. В этом случае положение точки М на кривой будет определяться длиной дуги AM кривой от начальной точки А до точки М. Пусть кривая АВ задана параметрическими уравнениями
x = x(s); |
|
|
], |
y = y(s); s [0, sAB |
|
|
|
z = z(s), |
|
где sAB |
— длина кривой АВ. Тогда функцию |
f (x, y, z) , определенную на |
|||
кривой |
АВ, |
можно рассматривать |
как |
сложную |
функцию |
f (x(s), y(s), z(s)) натурального параметра |
s . |
Выберем |
разбиение |
||
T ={A0 , A1 ,..., An} |
кривой АВ и точки Mi (xi , yi , zi ) |
на элементарных дугах |
|||
Ai−1 Ai этого разбиения. Составим соответствующую интегральную сумму. Пусть si есть значение натурального параметра для точки Ai , i = 0,1,..., n, a
si – значение |
натурального |
параметра для точки |
Mi , i =1,..., n. |
Тогда |
длины ∆si |
элементарных |
дуг Ai−1 Ai можно |
записать в |
виде, |
∆si = si − si−1 , i =1,..., n, а интегральную сумму представить следующим |
||||
образом:
n |
n |
∑ f (xi , yi , zi )∆si = ∑ f (x(si ), y(si ), z(si ))∆si . |
|
i=1 |
i=1 |
Правая часть равенства есть интегральная сумма, соответствующая определенному интегралу от функции f (x(s), y(s), z(s)) по отрезку [0, sAB ].
Переход к пределу в обеих интегральных суммах выполняется при одном
условии λ(T) = max ∆si → 0. Поэтому
i=1,...,n
sAB
∫f (x, y, z)ds = ∫ f (x(s), y(s), z(s))ds,
AB |
0 |
причем существование одного из интегралов в этом равенстве означает существование и другого. На основании этого, можно сформулировать достаточные условия существования криволинейного интеграла первого рода.
Теорема 1.1. Если кривая AB спрямляема, а функция f (x, y, z) непрерывна вдоль этой кривой, то криволинейный интеграл первого рода от функции
f (x, y, z) вдоль кривой AB существует.( Доказательство теоремы |
см, |
например,[1]). |
|
18
Свойства криволинейного интеграла первого рода, очевидно,
следуют из определения интеграла, как предела интегральных сумм, а именно:
свойства линейности
1) ∫ ( f (x, y, z) ± g(x, y, z))ds = ∫ f (x, y, z) ds ± ∫ g(x, y, z) ds;
AB |
|
AB |
AB |
2) ∫ k f (x, y, z) ds =k ∫ |
f (x, y, z) ds, |
( k – константа); |
|
AB |
AB |
|
|
3) (свойства аддитивности) если на кривой AB взята произвольная точка C , то ∫ f (x, y, z)ds = ∫ f (x, y, z)ds + ∫ f (x, y, z)ds;
AB |
AC |
CB |
4) ∫ f (x, y, z)ds = ∫ f (x, y, z)ds. |
|
|
AB |
BA |
|
В заключение отметим следующее. Так как криволинейный интеграл первого рода фактически есть определенный интеграл, на него переносятся основные свойства определенного интеграла: оценка интеграла по модулю (модуль интеграла не превосходит интеграла от модуля функции), теорема о среднем. В то же время понятия верхнего и нижнего пределов интегрирования, присущие определенному интегралу, не имеют аналогов для криволинейного интеграла, а известное свойство определенного интеграла менять знак, когда верхний и нижний пределы меняются местами, не распространяется на криволинейный интеграл первого рода.
1.1.2 Геометрический смысл криволинейного интеграла первого рода
Пусть кривая AB лежит в плоскости xOy. Непрерывная функция f (x, y) ≥ 0 в области определения. Построим цилиндрическую
поверхность с направляющей линией AB и образующими, параллельными оси Oz. В каждой точке M длину образующей сделаем равной значению f (M ) = f (x, y) . То есть цилиндрическая поверхность ограничена сверху
поверхностью z = f (x, y) (рис. 1.2.3).
Найдем площадь S |
построенной части цилиндрической поверхности. |
||||||
Если |
разбить кривую |
AB |
на части |
∆si , i =1,..., n, |
то |
поверхность |
|
S разобьется на узкие полосы Si , i =1,..., n. |
Площадь полосы Si приближенно |
||||||
равна площади прямоугольника с основанием ∆si |
и высотой |
f (Mi ), где |
|||||
Mi |
– произвольно |
взятая |
точка |
на дуге |
∆si . |
Следовательно, |
|
|
n |
|
|
|
|
|
|
S ≈ ∑ f (Mi )∆si . Пусть λ = max ∆si , тогда |
|
|
|
||||
i=1 |
i=1,...,n |
|
|
|
|
||
|
|
|
|
|
|
||
|
|
n |
|
|
|
|
|
|
S = limλ→0 ∑ f (Mi )∆si = ∫ f (M )ds = |
∫ f (x, y)ds. |
|
||||
|
|
i=1 |
AB |
|
AB |
|
|
19
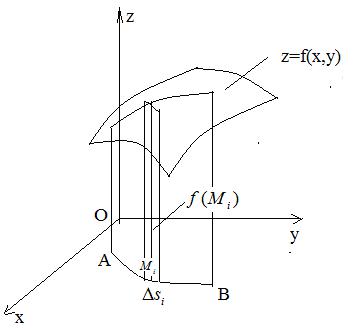
Рис. 1.2.3.
Таким образом, криволинейный интеграл первого рода ∫ f (x, y)ds на
AB
плоской кривой AB определяет площадь части цилиндрической поверхности с направляющей AB и образующей, параллельной оси Oz , ограниченной сверху поверхностью z = f (x, y). В частности, если
f (x, y) ≡1, то криволинейный интеграл ∫ ds = lAB определяет длину
AB
кривой AB .
1.1.3 Механические приложения криволинейного интеграла первого рода. Задача о массе материальной кривой
Пусть функция ρ(M ) = ρ(x, y, z) , определенная на кривой AB задает
линейную плотность распределения массы вдоль этой кривой. При |
мелком |
||||
разбиении кривой |
AB (см. рис. |
1.2.1) |
на большое |
число |
n N |
элементарных дуг |
Ai−1 Ai ,i =1,..., n, |
можно |
приближенно |
принять, что |
|
линейная плотность распределения массы во всех точках каждой элементарной дуги Ai−1 Ai постоянна и равна значению ρ(Mi ) линейной
плотности в произвольной точке Mi (xi , yi , zi ) этой дуги. Обозначим через ∆si длину элементарной дуги Ai−1 Ai . Тогда масса этой дуги определится следующим образом: mi ≈ ρ(Mi )∆si ,i =1,..., n. В этом случае для массы m всей кривой AB получим
m≈ ∑ρ(Mi )∆si .
i=1n
20
