
Ми10 крив и пов
.pdf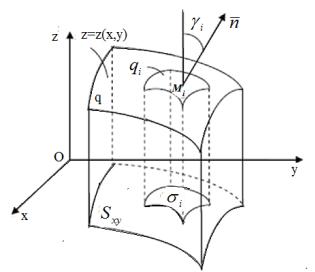
Если функция f (x.y, z) непрерывна вдоль кусочно-гладкой поверхности Q , то поверхностный интеграл первого рода существует.
(Доказательство теоремы смотрите, например,[3]).
Поверхностный интеграл первого рода обладает теми же свойствами,
что и двойной интеграл. В частности, выполняется свойство аддитивности: если поверхность Q разбита на части Q1 и Q2 , то
∫∫ f (x, y, z)dq = ∫∫ f (x, y, z)dq + ∫∫ f (x, y, z)dq.
Q |
Q1 |
Q2 |
Читателю предлагаем самостоятельно сформулировать остальные свойства.
2.2.1. Вычисление поверхностного интеграла I-го рода
Пусть задана гладкая поверхность Q уравнением z = z(x, y) . Так как поверхность гладкая, то z(x, y) – непрерывная функция вместе со своими частными производными. И пусть на поверхности Q определена непрерывная функция f (x, y, z) . Требуется вычислить поверхностный интеграл ∫∫ f (x, y, z)dq (Нельзя смешивать интегрируемую функцию f (x,
Q
y, z) с функцией, входящей в уравнение поверхности Q ).
Предварительно займемся выводом формулы для вычисления площади ∆qi элементарной части qi поверхности Q . Обратимся к рис. 2.2.2 и 2.2.3, где выделен участок qi разбиения области Q на элементарные части с выбранной на нем точкой Mi (xi , yi , z(xi , yi )) . Через точку Mi qi проведем касательную плоскость к поверхности Q . Уравнение касательной плоскости, как известно (формула (2.7)) , имеет вид
zx' (x, y) |Mi (x − xi ) + z'y (x, y) |Mi ( y − yi ) −(z − zi ) = 0.
Рис.2.2.2.
71
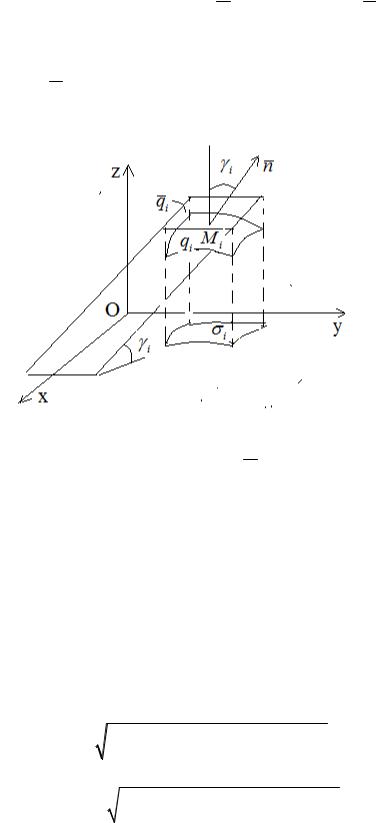
На этой плоскости выделим элемент qi с площадью∆qi (рис. 2.2.3), который проектируется на плоскость xOy в ту же элементарную область σi , что и элемент qi (рис. 2.13). Заменим криволинейный элемент qi
плоским элементом qi , тогда
∆qi ≈ ∆ |
qi |
. |
(2.11) |
Рис.2.2.3
Обозначим через γi двугранный угол между касательной плоскостью и плоскостью xOy. Следовательно, ∆σi = ∆qi | cosγi | ( как известно из
аналитической геометрии, площадь проекции плоской фигуры равна площади самой этой фигуры, умноженной на абсолютную величину косинуса двугранного угла между плоскостями). Откуда в силу формулы (2.11) получаем
∆q ≈ |
∆σi |
. |
(2.12) |
|
|||
i |
| cosγi | |
|
|
|
|
||
Линейный угол двугранного угла γi есть в то же время угол между осью
Oz и единичным вектором нормали n к касательной плоскости. И поэтому, см. формулу (2.8),
| cosγi |
|= |
|
|
|
1 |
. |
(2.13) |
|||
|
|
1 + |
(zx' (xi , yi ))2 +(z'y (xi , yi ))2 |
|||||||
|
|
|
|
|
|
|
|
|||
Таким образом, с учетом (2.12) и (2.13) получаем |
|
|
||||||||
∆qi ≈ |
∆σi |
|
|
= |
1 |
+(zx' (xi , yi ))2 +(z'y (xi , yi ))2 ∆σi . |
(2.14) |
|||
| cosγi | |
||||||||||
|
|
|
|
|
|
|
||||
А теперь, для решения поставленной задачи о вычислении поверхностного интеграла, вернемся к интегральной сумме (2.9), соответствующей данному разбиению поверхности Q на части ∆qi и выбору точек
72

Mi |
( i =1, 2,..., n). |
Принимая во внимание полученное выражение для ∆qi |
(2.14), запишем формулу (2.10) в виде: |
||
|
n |
n |
∫∫f(x, y,z)dq=limd→0 ∑f(xi, yi,zi )∆qi =limd→0 ∑f(xi, yi,z(xi, yi )) 1+(zx' (xi, yi ))2 +(z'y(xi, yi ))2∆σi. |
||
Q |
i=1 |
i=1 |
Очевидно, если d → 0 , ( d — максимальный из диаметров di частичных |
||
областей qi ,i =1,2,..., n,) то и δ → 0 , где δ – максимальный из диаметров
проекций σi , i =1, 2,..., n, частичных областей qi , |
на плоскость xOy (рис. |
|
2.13). Отсюда |
n |
|
|
|
|
∫∫ f (x, y, z)dq = limδ→0 |
∑f (xi , yi , z(xi , yi )) 1+(zx' (xi , yi ))2 |
+(z'y (xi , yi ))2 ∆σi . (2.15) |
Q |
i=1 |
|
Сумма, стоящая в правой части равенства (2.15), является интегральной
суммой |
для |
непрерывной |
функции |
|
f (x, y, z(x, y)) |
1 +(zx' (x, y))2 |
+(z'y (x, y))2 |
по плоской |
области Sxy – |
проекции поверхности Q |
на плоскость |
xOy . Поэтому |
ее предел есть |
|
двойной интеграл от указанной функции двух переменных по области Sxy . Следовательно,
∫∫ f (x, y, z)dq = ∫∫ f (x, y, z(x, y)) 1 +(zx' (x, y))2 +(z'y (x, y))2 dσ,
Q |
Sxy |
иначе |
|
∫∫ f (x, y, z)dq = ∫∫ f (x, y, z(x, y)) 1 +(zx' (x, y))2 +(z'y (x, y))2 dxdy. (2.16) |
|
Q |
Sxy |
Заметим, что существование двойного интеграла доказывает, в силу (2.16) существование поверхностного интеграла при оговоренных условиях, которым удовлетворяют подынтегральная функция и область интегрирования.
Если |
гладкая поверхность |
Q задана |
уравнением y = y(x, z) или |
||
x = x( y, z) , то проектируя поверхность Q , |
соответственно, на плоскости |
||||
xOz и yOz , из равенства (2.16), можно получить следующие формулы: |
|||||
∫∫ f (x, y, z)dq = ∫∫ f (x, y(x, z), z)) |
1 +(yx' (x, z))2 |
+(yz' (x, z))2 dxdz, |
(2.17) |
||
Q |
Sxz |
|
|
|
|
∫∫ f (x, y, z)dq = ∫∫ f (x( y, z), y, z)) |
1 +(x'y ( y, z))2 |
+(xz' ( y, z))2 dydz. |
(2.18) |
||
Q |
Syz |
|
|
|
|
где Sxz , Syz – проекции поверхности Q на координатные плоскости xOz и yOz .
Замечание. В более сложных случаях, когда поверхность кусочно-гладкая или неоднозначно проектируется на координатные плоскости, ее
73

разбивают на гладкие части, однозначно проектирующиеся на одну из координатных плоскостей, тогда интеграл разобьется на сумму интегралов по этим частям, к каждому из которых применимы формулы (2.16) – (2.18). Пример 2.3. Вычислить площадь Q части гиперболического параболоида
z = xy , вырезаемой прямым круговым цилиндром x2 + y2 = 8 (рис.2.2.4).
Рис.2.2.4 |
|
|
|
|
|
|
|
Решение. В данном случае поверхность |
является |
графиком |
функции |
||||
z(x, y) = xy с областью определения |
S |
xy |
= |
{ |
|
} |
В этой |
|
|
(x, y) :x2 + y2 ≤ 8 . |
|||||
области функция z(x, y) = xy непрерывна и имеет непрерывные частные производные zx' = y и z'y = x . Следовательно имеем (формула (2.10*)):
SQ = ∫∫dq = ∫∫ |
1 +(zx' (x, y))2 +(z'y (x, y))2 dxdy =∫∫ 1 + y2 + x2 dxdy. |
|
Q |
Sxy |
Sxy |
Для вычисления этого двойного интеграла удобно перейти к полярным координатам x = ρ cosϕ, y = ρsinϕ , в которых
dxdy = ρdρdϕ, Sxy |
→ D ={(ρ,ϕ) : ρ [0, 8],ϕ [0,2π]}. |
|
|
|||||||
Тогда получим |
|
|
|
|
|
|
|
|
|
|
SQ = ∫∫ 1 + y2 + x2 dxdy = |
2∫π dϕ ∫8 |
ρ 1+ ρ2 dρ = 2π |
(1 + ρ2 )3/ 2 |
|
|
8 |
52 |
π. |
||
|
||||||||||
|
|
= |
||||||||
3 |
3 |
|||||||||
Sxy |
0 |
0 |
|
|
|
0 |
|
|||
|
|
|
|
|
|
|||||
2.2.2. Механические приложения поверхностного интеграла первого рода
Пусть по поверхности Q распределена масса с поверхностной плотностью ρ(x, y, z) , представляющей собой непрерывную функцию на Q . Такую поверхность называют материальной поверхностью. Разобьем поверхность на n частичных областей qi ,i =1, 2,..., n, выбрав на каждой из них произвольную точку Mi (xi , yi , zi ) qi . При этом полагаем, что при малых диаметрах di частичных областей qi поверхностная плотность
74

распределенной по поверхности массы в пределах каждой частичной области постоянна и равна значению ρ(Mi ) = ρ(xi , yi , zi ) .
При этих предположениях, как и в случае материальной кривой (см. 1.2.3.), приходим к следующим выводам:
а) масса всей поверхности Q равна
|
|
mQ = ∫∫ρ(x, y, z)dq; |
|
|
|
(2.19) |
||||
|
|
|
Q |
|
|
|
|
|
|
|
б) статические моменты этой поверхности относительно |
|
|||||||||
координатных плоскостей yOz, xOz , и xOy равны |
|
|
|
|||||||
M yOz = ∫∫xρ(x, y, z)dq, MxOz = ∫∫yρ(x, y, z)dq, MxOy = ∫∫zρ(x, y, z)dq, |
(2.20) |
|||||||||
Q |
|
Q |
|
|
|
|
Q |
|
||
где x, y, z – координаты точки |
M Q; |
|
|
|
|
|
||||
в) координаты центра масс поверхности Q имеют вид |
|
|||||||||
x |
= |
M yOz |
, y = |
M |
xOz |
, z = |
MxOy |
|
; |
(2.21) |
|
|
|
|
|
||||||
C |
|
mQ |
C |
mQ |
C |
mQ |
|
|
|
|
|
|
|
|
|
|
|
||||
г) моменты инерции этой поверхности относительно, например, плоскости yOz , оси Ox и начала координат равны соответственно
JyOz = ∫∫x2 ρ(x, y, z)dq, JOx = ∫∫( y2 + z2 )ρ(x, y, z)dq,
Q Q
JO = ∫∫(x2 + y2 + z2 )ρ(x, y, z)dq.
Q
Аналогично выражаются моменты инерции относительно других осей. Пример 2.4. Вычислить статический момент относительно плоскости xOy и координаты центра масс однородной полусферы радиуса R .
Решение. Выберем систему координат так, чтобы полусфера стояла на плоскости xOy , а начало координат находилось в ее центре. Тогда
уравнение полусферы имеет вид x2 + y2 + z2 = R2 (z ≥ 0) .
На основании формулы (2.20), где полагаем ρ(x, y, z) =1, так как
полусфера однородная, имеем MxOy |
= ∫∫zdq. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Разрешим уравнение поверхности относительно z : z = |
|
R2 − x2 − y2 Тогда |
||||||||||||||||||
поверхность |
является |
графиком |
функции |
|
z(x, y) = |
R2 − x2 − y2 |
с |
|||||||||||||
областью определения |
Sxy ={(x, y) :x2 + y2 |
≤ R2 }. |
|
На |
основании |
с |
||||||||||||||
формулы (2.16) получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
MxOy = ∫∫zdq = ∫∫ R2 − x2 − y2 |
1+ |
|
|
|
x |
2 |
|
|
|
+ |
|
|
y |
2 |
|
|
dxdy = |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
R |
2 |
− x |
2 |
− y |
2 |
R |
2 |
− x |
2 |
− y |
2 |
|
|||||||
Q |
Sxy |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
75
= ∫∫ R2 − x2 − y2 |
|
|
R |
|
|
|
dxdy = R∫∫dxdy =R πR2 =πR3 . |
R |
2 |
− x |
2 |
− y |
2 |
||
Sxy |
|
|
|
Sxy |
Так как материальная сфера однородная, то из соображений симметрии ее центр тяжести должен находиться на оси Oz , поэтому xC = 0, yC = 0 , а
zC = MxOy . По формуле (2.19) найдем массу полусферы mQ
mQ = ∫∫dq = ∫∫ |
1 + |
|
|
x2 |
|
|
+ |
|
|
y2 |
|
|
dxdy =∫∫ |
|
|
R |
|
|
|
dxdy. |
|||
R |
2 |
− x |
2 |
− y |
2 |
R |
2 |
− x |
2 |
− y |
2 |
R |
2 |
− x |
2 |
− y |
2 |
||||||
Q |
Sxy |
|
|
|
|
|
|
|
|
Sxy |
|
|
|
|
|||||||||
Для вычисления двойного интеграла перейдем к полярным координатам: x = ρ cosϕ, y = ρsinϕ , в которых
dxdy = ρdρdϕ, Sxy → D ={(ρ,ϕ) : ρ [0, R],ϕ [0, 2π]}.
Тогда
|
|
|
R |
|
|
|
dxdy = R2∫π dϕ∫R |
|
|
ρdρ |
|
= −R2∫π |
|
R |
|||
mQ = ∫∫ |
|
|
|
|
|
|
|
|
R2 − ρ2 |
dϕ = 2πR2 . |
|||||||
|
2 |
2 |
|
2 |
|
|
|
2 |
2 |
||||||||
Sxy |
R |
|
− x |
− y |
|
|
MxOy |
|
0 0 |
|
R − ρ |
|
0 |
|
0 |
||
|
|
|
|
|
|
||||||||||||
Таким образом, |
z = |
|
= |
πR3 |
= |
|
R |
. |
|
|
|
|
|||||
|
m |
2πR2 |
2 |
|
|
|
|
||||||||||
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
2.3. Поверхностный интеграл второго рода |
|
|||||||||||||
|
|
|
|
|
|
|
2.3.1. Векторные поверхности |
|
G |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть в пространственной области Q задано векторное поле a(M ) .
Возьмем в |
Q гладкую кривую |
L, для которой в любой ее точке |
M |
|
касательныйG вектор кривой не является коллинеарным вектору |
G |
(в |
||
a(M ) |
||||
частности, |
a(M ) ≠ 0G). Такую кривую будем называть трансверсалъной |
|||
векторному |
полю a(M ) . Через |
каждую точку M L можно |
провести |
|
векторную линию рассматриваемого поля. При этом множество всех таких линий, проходящих через точки M L , образует поверхность S G(Рис.
2.3.1), называемую векторной поверхностью векторного поля a(M ) .
Векторная линия, проходящая через любую точку M S векторной поверхности S , целиком лежит на этой поверхности. ПоэтомуGкасательная
к векторной линии в точке M S , а значит, и вектор a(M ) будут
JJJJG
перпендикулярны единичному вектору n(M ) нормали к S в этой точке
76

Рис. 2.3.1
Выбрав в качестве кривой L простой замкнутый контур, получим векторнуюG поверхность, называемую векторной трубкой векторного
поля a(M ) (Рис. 2.3.2). Любая векторная линия, не проходящая через точки контура L, целиком лежит либо внутри, либо вне векторной трубки.
Рис. 2.3.2
2.3.2. Задача о потоке векторного поля. Понятие поверхностного интеграла II-го рода
Пусть в пространственной области Ω задано векторное поле |
|||
JJJJJJG |
G |
G |
G |
F(M ) = X (x, y, z) i |
+Y(x, y, z) j +Z(x, y, z) k , где X = X (x, y, z); |
||
Y =Y(x, y, z); |
Z = Z(x, y, z) – непрерывные функции. |
||
Рис. 2.3.3
77
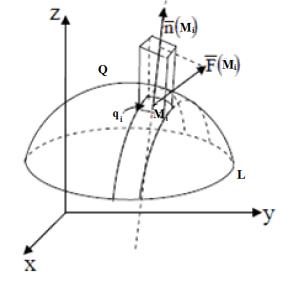
На гладкой двусторонней поверхности Q Ω, ограниченной гладким замкнутым контуром L, выберем одну из сторон поверхности Q с
помощью единичного |
вектора |
нормали |
n(M ) к этой поверхности. |
Координатами вектора |
G |
являются |
его направляющие косинусы |
n(M ) |
cosα,cos β,cosγ , определяемые формулой (2.8) (Рис.2.3.3) .
JJJJJJG
Вектор F(M ) может определять направление скоростей: потока жидкости,
потока воздуха, потока частиц газа, магнитных полей и т.д. Пусть, для
JJJJJJG
определенности, вектор F(M ) определяет скорость потока жидкости, протекающей через поверхность Q . Разобьем поверхность Q
произвольным образом на n элементарных частей, площадь которых обозначим через ∆qi . На каждой из частей qi выберем произвольную
точку |
|
|
M |
(x , y , z ) , |
и вычислим |
значение |
вектора |
скорости |
жидкости |
|||||||||||
JJJJJJJG |
|
i |
i i |
i |
Если выбранное разбиение поверхности Q достаточно |
|||||||||||||||
F(M |
) |
|
(Рис.2.3.4). |
|||||||||||||||||
i |
|
|
|
|
|
|
|
|
|
|
что значение вектора скорости |
JJJJJJG |
на |
|||||||
мелкое, то можно допустить, |
F(M ) |
|||||||||||||||||||
площадке |
qi |
|
постоянное |
|
и |
|
|
JJJJJJG |
|
Рассмотрим |
скалярное |
|||||||||
|
|
равно F(Mi ) . |
|
|||||||||||||||||
|
|
|
|
|
|
JG |
|
G |
|
)) |
векторов |
|
JJJJJJG |
и |
n(M |
) . |
Так |
как |
||
произведение (F(M |
), n(M |
|
F(M |
) |
||||||||||||||||
JG |
|
|
G |
|
)) | ∆q |
i |
|
i |
|
|
|
|
i |
|
|
i |
|
|
|
|
| (F(M |
|
), n(M |
можно рассматривать как объем призмы с площадью |
|||||||||||||||||
|
|
i |
|
i |
|
i |
|
|
|
G |
G |
)) | (Рис.2.3.4), то произведение |
||||||||
основания |
∆q |
и высотой |
| (F(M |
), n(M |
||||||||||||||||
JG |
|
|
G |
|
i |
|
|
|
|
|
i |
i |
|
|
|
|
|
|
|
|
(F(Mi ), n(Mi ))∆qi |
приближенно |
определяет |
|
количество |
жидкости, |
|||||||||||||||
протекающей через площадку qi за единицу времени в направлении вектора нормали n(Mi )
Рис.2.3.4
78
Тогда общее количество жидкости, протекающей в единицу времени через
поверхность Q в направлении вектора нормали n(M ) к поверхности Q ,
JJJJJJG
что естественно назвать потоком PQ |
векторного поля F(M ) |
через |
|
n |
JG |
G |
|
поверхность Q , приближенно равно ∑(F(Mi ), n(Mi ))∆qi , то есть |
|
||
i=1 |
G |
|
|
n JG |
|
|
|
PQ ≈ ∑(F(Mi ), n(Mi ))∆qi . |
(2.20) |
||
i=1
Сумма (2.20) называется интегральной суммой. При различных разбиениях поверхности Q на элементарные части qi ,i =1, 2,..., n, и различном выборе
точек Mi |
qi |
получаем различные значения интегральной суммы (2.20). |
||||
Пусть d |
– |
максимальный |
из |
диаметров |
di частичных |
областей |
qi ,i =1, 2,..., n. |
Естественно |
в |
качестве |
точного значения |
потока |
|
векторного поля принять предел интегральных сумм в правой части (2.20)
при d → 0, |
т.е. |
|
JG |
G |
JG |
G |
|
|
|
n |
|
||||
PQ |
= limd →0 |
∑(F(Mi ) n(Mi ))∆qi |
= ∫∫(F(M ) n(M ))dq, |
(2.21) |
|||
|
|
i=1 |
|
|
Q |
|
|
который не зависит ни от способа разбиения, ни от выбора точек Mi qi .
Интеграл, стоящий в правой части формулы (2.21), как известно, представляет собою поверхностный интеграл первого рода.
Замечание 2.3.1. Если поверхность Q является поверхностью векторной
JJJJJG
трубки |
векторного поля F(M ) , то |
поток векторного поля через |
|||||||
поверхность Q |
|
равен нулю, так как, в этом случае, |
JJJJJJG |
||||||
|
векторы F(M ) и |
||||||||
G |
|
|
|
|
|
|
|
|
|
n(M ) ортогональны. |
|
|
|
||||||
|
Таким образом, нахождение потока векторного поля привело нас к |
||||||||
нахождению предела интегральных сумм вида (2.20) . |
|
||||||||
|
|
|
G |
|
|
|
|
|
|
|
Так |
какG n(Mi ) = (cosαi ,cos βi ,cosγi ) , |
где αi , βi и |
γi – углы между |
|||||
вектором |
n(M |
i |
) |
и направлениями осей |
Ox,Oy и Oz соответственно, |
||||
JJJJJJJG |
|
|
|
|
|
|
|
||
F(Mi ) |
= (X (Mi ),Y(Mi ), Z(Mi )) , то |
|
|
||||||
|
n |
JG |
G |
|
|
|
n |
|
|
lim |
∑(F(Mi ) n(Mi ))∆qi =lim∑(X(Mi )cosαi +Y(Mi )cos βi |
+ Z(Mi )cosγi )∆qi = |
|||||||
d→0 |
i=1 |
|
|
|
|
d→0 |
i=1 |
G |
G |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
=∫∫(X(x, y, z)cosα +Y(x, y, z)cosβ +Z(x, y, z)cosγ)dq =∫∫(F(M) n(M))dq. (2.22) |
|||||||||
Q |
|
|
|
|
|
|
|
Q |
|
79
n
Рассмотрим предел интегральной суммы lim ∑Z(Mi )cosγi∆qi . Как
d →0 i=1
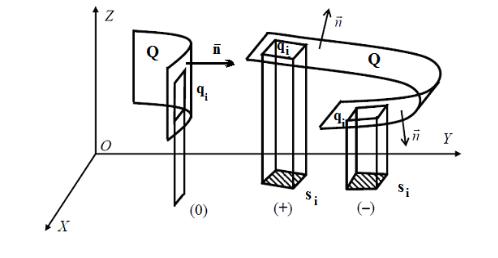
известно, угол γi между вектором n(Mi ) и осью Oz равен углу между площадкой разбиения qi и плоскостью xOy (рис. 2.2.3).
|
|
Рис.2.3.5 |
Тогда cosγi∆qi |
= ∆si , где | ∆si | – площадь проекции si площадки разбиения |
|
q в плоскость |
xOy (рис. 2.3.5). Здесь ∆s берется со знаком плюс, если |
|
i |
G |
i |
угол между вектором n(Mi ) |
и осью Oz острый, и со знаком минус, если |
|
угол тупой (рис. 2.3.5). Так как предел интегральной суммы (2.21), если он существует, не зависит от способа разбиения, то мы можем разбить поверхность Q плоскостями, параллельными координатным плоскостям.
Тогда cosγi∆qi = ∆si = ∆xi∆yi и
n
lim ∑
d →0 i=1
n
Z(Mi )cosγi∆qi = lim ∑Z(xi , yi , zi )∆xi∆yi . (2.22*)
d →0 i=1
Если |
предел |
интегральных |
сумм |
|
n |
|
, |
где |
d – |
lim ∑Z(xi , yi , zi )∆xi∆yi |
|||||||||
|
|
|
|
d →0 |
i=1 |
|
|
|
|
|
|
|
di |
|
|
qi ,i =1, 2,..., n, |
|||
максимальный |
из диаметров |
частичных |
областей |
||||||
существует, не зависит от способа разбиения поверхности Q |
и выбора |
||||||||
точек |
Mi (xi , yi , zi ) , то такой предел называется поверхностным |
||||||||
интегралом второго рода ∫∫Z(x, y, z)dxdy. То есть |
|
|
|
||||||
|
|
Q |
|
|
|
|
|
|
|
|
|
n |
|
|
|
n |
|
|
|
∫∫Z(x, y, z)dxdy = limd →0 ∑Z(xi , yi , zi )∆xi∆yi = limd →0 ∑Z(Mi )cosγi∆qi |
= |
||||||||
Q |
|
i=1 |
|
|
|
i=1 |
|
|
|
|
|
= ∫∫Z(x, y, z)cosγdq. |
|
|
|
(2.23*) |
|||
|
|
Q |
|
|
|
|
|
|
|
80
