
Ми10 крив и пов
.pdf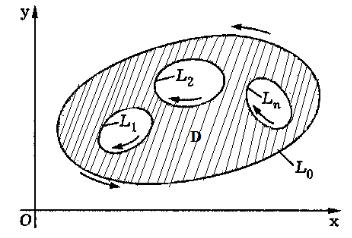
Если функции X (x, y) и Y(x, y) непрерывны в D вместе со своими частными производными, то верна формула Грина для многосвязной
области |
|
|
|
|
|
>∫ |
|
∂Y |
|
∂X |
|
X (x, y)dx +Y(x, y)dy = ∫∫ |
− |
dxdy, |
|||
∂D |
D |
∂x |
|
∂y |
|
где символ >∫ |
(криволинейный интеграл |
|
по |
границе замкнутой |
|
∂D
∂D области) обозначает сумму криволинейных интегралов по всем контурам, составляющим границу D , каждый из которых обходится в положительном направлении.
Рис.1.3.8
Пример 1.13. Вычислить криволинейный интеграл
>∫(x + y)2 dx −(x − y)2 dy
L
по замкнутому контуру L , образованный синусоидой y = sin x и отрезком
оси Ox, x [0;π]. |
|
|
|
|
Решение. Воспользуемся формулой Грина. Так как |
|
|
||
X (x, y) = (x + y)2 ;Y(x, y) = −(x − y)2 , то |
∂X(x, y) =2(x + y); |
∂Y(x, y) |
=−2(x− y). |
|
|
|
∂y |
∂x |
|
>∫(x + y)2 dx −(x − y)2 dy = ∫∫( − 2(x − y) − 2(x + y))dxdy = −4∫∫xdxdy. |
||||
L |
D |
|
D |
|
Область D ограничена замкнутым контуром L : y = 0, y = sin x, x = 0, x =π .
Следовательно
>∫(x + y)2 dx −(x − y)2 dy = −4π∫xdxsin∫x dy = −4π∫xsin xdx =
L |
|
|
0 |
0 |
0 |
= −4(−xcos x +sin x) |
|
π |
|
= −4(π + 0) = −4π. |
|
|
|
||||
|
|
0 |
|
|
|
|
|
|
|
|
|
41
1.2.7. Условия независимости криволинейного интеграла от пути интегрирования
Пусть в некоторой области D в плоскости xOy заданы непрерывные функции X (x, y) и Y(x, y) . Рассмотрим криволинейный интеграл второго
рода |
|
∫ X (x, y)dx +Y(x, y)dy, |
(1.27) |
AB |
|
где АВ — произвольная кусочно гладкая кривая, целиком лежащая в D и соединяющая точки A и B этой области. Выясним, при каких условиях криволинейный интеграл не зависит от пути интегрирования, а зависит лишь от положения точек A и B .
Теорема 1.4. Для того чтобы значение криволинейного интеграла (1.27) в области D не зависело от пути интегрирования, необходимо и
достаточно, чтобы для любого замкнутого контура |
L в D |
выполнялось равенство |
|
v∫X (x, y)dx +Y(x, y)dy = 0. |
(1.28) |
L |
|
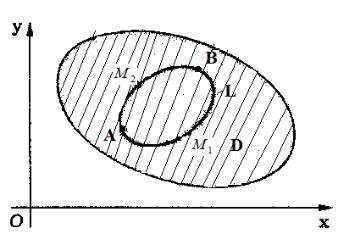
Доказательство. Необходимость. Предположим, что значение криволинейного интеграла (1.27) не зависит от пути интегрирования. Произвольный контур L, целиком лежащий в D , двумя произвольными точками A и B разделим на две кривые AM1B и AM2 B (рис. 1.3.9).
Рис.1.3.9
Так как криволинейный интеграл (1.27) не зависит от пути интегрирования, имеем:
∫ X (x, y)dx +Y(x, y)dy = ∫ X (x, y)dx +Y(x, y)dy.
AM1B AM2 B
Отсюда, на основании свойств криволинейного интеграла второго рода, получаем
42
v∫X (x, y)dx +Y(x, y)dy = ∫ X (x, y)dx +Y(x, y)dy + ∫ X (x, y)dx +Y(x, y)dy =
L |
AM1B |
BM2 A |
= ∫ X (x, y)dx +Y(x, y)dy − ∫ X (x, y)dx +Y(x, y)dy = 0. |
||
AM1B |
AM2 B |
|
Достаточность. Пусть равенство (1.28) |
выполнено для любого контура L, |
|
целиком лежащего в области D. Выберем произвольные точки A и B в области D и соединим их двумя различными кривыми AM1B и AM2 B,
целиком лежащими в D. Из этих кривых можно составить контур L (рис. 1.3.9). Тогда, на основании свойств криволинейного интеграла второго рода и формулы (1.28) , имеем:
v∫X (x, y)dx +Y(x, y)dy = ∫ X (x, y)dx +Y(x, y)dy + ∫ X (x, y)dx +Y(x, y)dy = 0.
L AM1B BM2 A
Так как при изменении направления обхода кривой криволинейный интеграл второго рода меняет знак, из последнего равенства следует, что
∫ X (x, y)dx +Y(x, y)dy = ∫ X (x, y)dx +Y(x, y)dy.
AM1B AM2 B
В силу произвольности выбора кривых, связывающих точки A и B,
заключаем, что криволинейный интеграл в области D не зависит от пути интегрирования.
Пусть в области D криволинейный интеграл второго рода не зависит от пути интегрирования. Тогда его значение определяется лишь начальной точкой A и конечной точкой B пути интегрирования. Учитывая это, такой интеграл записывают в виде
∫B X (x, y)dx +Y(x, y)dy,
A
рассматривая точки A и B как нижний и верхний пределы интегрирования. Зафиксируем точку A(x0 , y0 ) D. Тогда криволинейный
интеграл от точки A до произвольной точки M (x, y) определяет в области D функцию
|
( x, y) |
|
|
|
|
u(x, y) = ∫ |
X (x, y)dx +Y(x, y)dy. |
(1.28) |
|
(GВ дальнейшем |
( xo , y0 ) |
|
|
|
мы докажем, если задано |
векторное |
поле |
||
a = ( X (x, y),Y(x, y)) , |
интеграл |
от которого ∫ X (x, y)dx +Y(x, y)dy |
не |
|
AB
зависит от пути интегрирования, то такое поле является потенциальным полем. Функция u(x, y) , определяемая формулой (1.28), в этом случае,
называется потенциалом векторного поля.)
43
С помощью этой функции значение криволинейного интеграла можно вычислить для любой пары точек M1 (x1 , y1 ), M2 (x2 , y2 ) D , а именно
( x2 , y2 ) |
|
|
∫ |
X (x, y)dx +Y(x, y)dy = u(x2 , y2 ) −u(x1 , y1 ). |
(1.29) |
( x1 , y1 ) |
|
|
Действительно, путь интегрирования от точки M1 (x1 , y1 ) до точки M2 (x2 , y2 ) можно выбрать так, что он будет проходить через точку A.
Тогда в силу свойства аддитивности интеграл можно представить как сумму двух интегралов, первый – от точки M1 (x1 , y1 ) до точки A, а второй
– от точки A до точки M2 (x2 , y2 ) . Значение первого интеграла с учетом направления будет равно −u(x1 , y1 ), значение второго будет равно
u(x2 , y2 ).
Формулу (1.29) по аналогии с определенным интегралом часто называют формулой Ньютона — Лейбница для криволинейного
интеграла.
Теорема 1.5. Если функции X (x, y) и Y(x, y) непрерывны в области D , а
криволинейный интеграл второго рода от этих функций в области D не зависит от пути интегрирования, то функция u(x, y), определяемая
равенством (1.28), имеет в D непрерывные частные производные, причем
∂u(x, y) = X (x, y), ∂u(x, y) =Y(x, y), (x, y) D.
∂x ∂y
Доказательство. Пусть M (x, y) – произвольная точка области D .
Выберем δ > 0 настолько малое, что δ – окрестность точки M целиком попадает в область D. Для произвольного приращения
∆x, удовлетворяющего неравенству | ∆x |<δ, согласно формуле Ньютона-
Лейбница, имеем
( x+∆x, y)
∆xu = u(x + ∆x, y) −u(x, y) = ∫ X (x, y)dx +Y(x, y)dy,
( x, y)
причем в качестве пути интегрирования в последнем интеграле можно взять горизонтальный отрезок (независимость пути), соединяющий точки
k
M (x, y) и M (x + ∆x, y) (рис. 1.3.10).
44
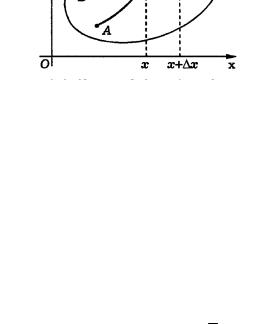
Рис.1.3.10
( x+∆x, y)
В этом случае dy = 0, и ∆xu = ∫ X (x, y)dx. Последний интеграл
( x, y)
является обычным определенным интегралом от функции одного переменного x ( y не меняется) по отрезку [x, x + ∆x]. По теореме о
среднем значении определенного интеграла получаем
( x+∆x, y)
∆xu = ∫ X (x, y)dx = X (x, y)∆x.
|
|
|
|
( x, y) |
|
|
|
|
|
|
|
|
|
|
Здесь |
|
[x, x + ∆x]. |
Когда |
∆x → 0, |
|
точка ( |
|
, y) → (x, y) и по |
||||||
x |
x |
|||||||||||||
непрерывности функции X (x, y) значение X ( |
|
, y) → X (x, y). Имеем |
||||||||||||
x |
||||||||||||||
|
|
∂u = lim |
∆xu |
= lim |
X ( |
|
, y)∆x |
= X (x, y). |
||||||
|
|
x |
||||||||||||
|
|
∆x |
|
|
|
|
||||||||
|
|
∂x |
∆x→0 |
∆x→0 |
∆x |
|||||||||
Итак, мы доказали, что ∂u |
= X (x, y) в каждой точке M (x, y) D. Точно так |
|||||||||||||
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
же доказывается, что |
∂u =Y(x, y). |
|
|
|
|
|
|
|
||||||
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
Замечание. |
|
Если функции X (x, y),Y(x, y) — координаты векторного поля |
||||||
G |
|
|
|
G |
|
G |
|
|
a = |
X (x, y)i |
+Y(xG, y) j , удовлетворяют условиям теоремы 1.5., то |
||||||
векторное поле a потенциально, так как выполняется равенство |
||||||||
G |
∂u G |
+ |
∂u G JJJJJG |
' |
' |
|||
a = |
∂x |
i |
∂y |
j = grad |
(ux |
,uy ). Функцию u(x, y), определяемую формулой |
||
|
|
|
|
|
|
|||
(1.28) называются потенциалом векторного поля.
Теорема 1.6. Пусть функции X (x, y) и Y(x, y) непрерывны вместе со
своими частными производными в некоторой односвязной области D в плоскости xOy . Тогда следующие четыре условия эквивалентны:
1) выражение X (x, y)dx +Y(x, y)dy |
является в области D полным |
||
дифференциалом некоторой функции u(x, y); |
|
|
|
2) всюду в области D верно равенство |
|
|
|
∂X (x, y) = |
∂Y(x, y) |
; |
(1.30) |
∂y |
∂x |
|
|
45 |
|
|
|
3) для любого контура L, лежащего в области D , верно равенство v∫X (x, y)dx +Y(x, y)dy = 0;
L
4) криволинейный интеграл второго рода от функций X (x, y) и Y(x, y)
в области D не зависит от пути интегрирования.
Доказательство. Будем доказывать теорему по следующей схеме: 1) →2) →3) →4) →1).
Сначала покажем, что 1) →2). Пусть
X (x, y)dx +Y(x, y)dy = du(x, y).
Тогда имеем |
∂u |
= X (x, y) и |
∂u =Y(x, y). Следовательно, |
|
||||||
|
∂x |
|
|
|
∂y |
|
|
|
|
|
|
|
∂X (x, y) |
= |
∂2u(x, y) |
и |
∂Y(x, y) |
= |
∂2u(x, y) |
. |
|
|
|
∂y |
|
∂y∂x |
∂x |
∂x∂y |
||||
|
|
|
|
|
|
|
||||
В силу непрерывности частных производных ∂X (x, y) и ∂Y(x, y)
∂y ∂x
(1.31)
правые
части последних равенств равны между собой, так как непрерывные смешанные производные не зависят от порядка дифференцирования. Поэтому равны и левые части этих равенств, т.е. выполнено второе условие теоремы.
Покажем теперь, 2) →3) . Пусть L – произвольный контур, лежащий в области D . На основании формулы Грина ,
>∫ |
|
∂Y(x, y) |
|
∂X (x, y) |
|
X (x, y)dx +Y(x, y)dy = ∫∫ |
− |
dxdy = 0, |
|||
∂D |
D |
∂x |
|
∂y |
|
так как в силу второго условия теоремы подынтегральная функция в двойном интеграле тождественно равна нулю. Итак, доказано, что выполнено третье условие теоремы.
Третье и четвертое условия эквивалентны в силу теоремы 1.4.
Докажем, что 4) →1). Пусть выполнено четвертое условие. Согласно теореме 1.5, функция u(x, y) , определяемая равенством (1.28), имеет
непрерывные частные производные, равные X (x, y) и Y(x, y). Но тогда эта
функция дифференцируема, а ее дифференциал имеет вид du(x, y) = X (x, y)dx +Y(x, y)dy.
Это доказывает выполнение первого условия теоремы. |
|
||||||
Замечание. |
Если |
X (x, y) и Y(x, y) |
– |
координаты векторного |
поля |
||
G |
G |
|
G |
удовлетворяющие |
условиям теоремы 1.6. |
, то |
|
a = X (x, y)i |
+Y(x, y) j, |
||||||
векторное |
|
поле |
aG |
потенциально |
тогда и только тогда, |
когда |
|
выполняется один из пунктов теоремы 1.6. |
G |
G |
Следствие. Циркуляция потенциального поля a = X (x, y)i |
+Y(x, y) j вдоль |
|
замкнутого контура равна нулю.
46

Теорема 1.6 дает не только несколько критериев независимости криволинейного интеграла от пути интегрирования, но и метод, позволяющий восстановить функцию u(x, y) по ее дифференциалу
X (x, y)dx +Y(x, y)dy.
1.2.8. Нахождение функции по ее полному дифференциалу
Если функции X (x, y) и Y(x, y) |
имеют в односвязной области |
D |
|||
непрерывные |
частные производные и |
∂X (x, y) = |
∂Y(x, y) , (x, y) D, |
то |
|
|
|
|
∂y |
∂x |
|
выражение |
X (x, y)dx +Y(x, y)dy = du(x, y) является дифференциалом |
||||
некоторой |
функции |
u(x, y) , определяемой |
равенством (1.28): |
||
( x, y) |
|
|
|
|
|
u(x, y) = ∫ |
X (x, y)dx +Y(x, y)dy (см. доказательство теоремы 1.6 пункт 4) |
||||
( xo , y0 )
→1)).
Очевидно, что все функции, имеющие один и тот же дифференциал X (x, y)dx +Y(x, y)dy, отличаются друг от друга постоянными слагаемыми.
Поэтому любая такая функция u(x, y) задается формулой
B( x, y)
u(x, y) = ∫ X (x, y)dx +Y(x, y)dy +C,
A( xo , y0 )
где C – произвольная постоянная.
Согласно теореме 1.6 в односвязной плоской области D криволинейный
B( x, y)
интеграл второго рода ∫ X (x, y)dx +Y(x, y)dy не зависит от пути
A( xo , y0 )
интегрирования. Основная идея в вычислении таких интегралов состоит в выборе наиболее простого пути интегрирования. Как правило, в этом случае в качестве пути интегрирования выбирают ломаную, звенья которой параллельны осям координат: по AM2 B или AM1B (рис. 1.3.11).
Рис.1.3.11
47
Если путь интегрирования AM2 B целиком попадает в область D , то в
соответствии со свойством 3 криволинейного интеграла второго рода можно написать
B( x, y)
u(x, y) = ∫ X (x, y)dx +Y(x, y)dy +C =
A( xo , y0 )
= ∫ X (x, y)dx +Y(x, y)dy + ∫ X (x, y)dx +Y(x, y)dy +C .
|
AM 2 |
|
M2 B |
|
|
|
|
|
Так как |
на |
отрезке |
AM2 имеем |
y = y0 , dy ≡ 0, x [x0 , x], |
а |
при |
||
интегрировании |
по |
отрезкуM2 B |
– |
x = x |
( x не |
меняется), |
||
dx ≡ 0, y [ y0 , y], то |
|
|
|
|
|
|
||
|
B(x, y) |
|
|
x |
|
y |
|
|
u(x, y) = |
∫ |
X(x, y)dx +Y(x, y)dy +C = ∫X(x, y0 )dx + ∫Y(x, y)dy +C. |
(1.32) |
|||||
|
A(xo , y0 ) |
|
|
x0 |
|
y0 |
|
|
Аналогично, если выбран путь интегрирования AM1B , то |
|
|
||||||
B( x, y) |
|
y |
|
x |
|
|
|
|
u(x, y) = ∫ |
X (x, y)dx +Y(x, y)dy +C = ∫Y(x0 , y)dy + ∫X (x, y)dx +C. |
(1.33) |
||||||
A( xo , y0 ) |
|
y0 |
G |
G x0 |
|
|
|
|
Пример 1.14. Дано векторное поле a = 2xyi |
+ x2 j . |
|
|
|
||||
|
|
G |
|
|
|
|
|
|
1)Доказать, что поле a потенциально.
2)Найти его потенциал с помощью криволинейного интеграла 2-го рода.
(0,4)
3) Вычислить: ∫ 2xydx + x2 dy .
(1,2) |
|
|
|
|
|
|
Решение. 1) Так как X (x, y) = 2xy;Y(x, y) = x2 , то |
∂X |
= |
∂Y |
= 2x. |
||
G |
|
G |
∂y |
|
∂x |
|
+ x2 |
|
|
|
|
||
Следовательно, векторное поле a = 2xyi |
j потенциально. |
|||||
2) Потенциал поля находим по формуле (1.32). Зададим координатам x0 и y0 точки A(x0 , y0 ) значения, равными нулю. Очевидно, в окрестности
точки |
A(0,0) частные производные |
∂X |
, |
∂Y |
непрерывны. Имеем: |
|
|
∂y |
|
∂x |
|
|
B( x, y) |
|
|
x |
y |
u(x, y) = ∫ X (x, y)dx +Y(x, y)dy +C = ∫X (x,0)dx + ∫Y(x, y)dy + C = |
|||||
|
A(0,0) |
|
|
0 |
0 |
xy
=∫2x 0dx + ∫x2 dy +C = x2 y +C .
0 |
0 |
3) Так как векторное поле потенциально, то верна формула НьютонаЛейбница для криволинейного интеграла
48

( x2 , y2 ) |
|
|
|
|
∫ |
X (x, y)dx +Y(x, y)dy = u(x2 , y2 ) −u(x1 , y1 ). |
|
|
|
( x1 , y1 ) |
|
|
|
|
(0,4) |
|
|
|
|
Следовательно, ∫ |
2xydx + x2 dy = u(0,4) −u(1,2) = 0 4 −1 2 = −2 . |
|
||
(1,2) |
|
|
|
|
Пример 1.15. Найти функцию u(x, y) , если |
|
|
|
|
du(x, y) = (3x2 − 2xy + y2 )dx −(x2 − 2xy +3y2 ) . |
|
|
||
Решение. Так как |
X (x, y) = 3x2 − 2xy + y2 ∂X (x, y) = −2x + 2 y; |
|
||
|
∂y |
|
|
|
Y(x, y) = −(x2 − 2xy +3y2 ) ∂Y(x, y) = −2x + 2 y , то |
∂X (x, y) ≡ |
∂Y(x, y) |
во |
|
|
∂x |
∂y |
∂x |
|
всей плоскости. Следовательно, выражение |
|
|
|
|
|
(3x2 − 2xy + y2 )dx −(x2 − 2xy +3y2 ) |
|
|
|
на всей плоскости xOy является полным дифференциалом. Полагая, что |
|
|||
x0 = 0, y0 = 0 в равенстве (1.32), получаем |
|
|
|
|
x |
y |
|
|
|
u(x, y) =∫3x2 dx − ∫(x2 − 2xy +3y2 )dy = x3 − x2 y + xy2 − y3 + C . |
|
|||
0 |
0 |
|
|
|
Задачи к главе 1.
1.1. Вычислить следующие криволинейные интегралы первого рода
∫ f (M )ds :
L |
от функции f (M ) = x + y , |
L – граница треугольника |
с вершинами |
||
а) |
|||||
A(0,0), B(1,0) |
и C(0,1) ; |
|
|
|
|
б) от функции f (M ) = y2 , L – |
арка циклоиды |
|
|||
|
|
x = a(t −sin t), y = a(1 −cost), t [0,2π]; |
|
||
в) от функции |
f (M ) = |
x2 + y2 , L – окружность x2 + y2 = ax; |
|||
г) от функции |
f (M ) = z, |
L – коническая винтовая линия |
|
||
|
|
x = t cost, y = t sin t, z = t,t [0,2π]; |
|
||
д) |
f (M ) = x + 4 y, , L – правая петля лемнискаты r2 = cos 2ϕ . |
|
|||
1.2. Найти массу материальной кривой L с линейной плотностью |
|||||
ρ = const : |
|
|
|
|
|
а) |
L: x = e−t cost, y = e−t sin t, z = e−t , t [0,ln 3] ; |
|
|||
б) |
L : x = 3t, y = 3t2 , z = 2t3 (дуга кривой между началом |
координат и |
|||
точкой A(3;3;2) ).
49

1.3. |
Найти |
массу материальной |
кривой |
L : |
|
x2 |
+ |
y2 |
|
=1, y ≤ 0 (нижняя |
||
9 |
4 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||
половина эллипса), имеющей линейную плотность ρ(M ) = −y. |
||||||||||||
1.4. Найти координаты центра масс однородной кривой L –: меньшей дуги |
||||||||||||
окружности x2 + y2 = 4 , заключенной между точками A(2;0) |
и B(−1; 3) . |
|||||||||||
1.5. |
Для |
однородной |
дуги |
астроиды, |
|
заданной |
соотношениями |
|||||
x2/3 + y2/3 = a2/3 , x ≥ 0, y ≥ 0 , |
найти координаты |
вектора |
статического |
|||||||||
момента, если линейная плотность дуги равна ρ .
1.6. Найти моменты инерции относительно осей координат одного витка
однородной винтовой линии x = cost, y = sin t, z = |
t |
, t [0;2π], если ее |
|
2π |
|||
линейная плотность равна ρ . |
|
||
|
|
1.7. Вычислить следующие криволинейные интегралы второго рода для указанных подынтегральных выражений:
а) (4x + y)dx + (x + 4 y)dy вдоль кривой AB : y = x4 , с концевыми точками
A(0;0) и B(−1;1) ;
б) (x + y)dx + (x − y)dy вдоль окружности (x −1)2 + ( y −1)2 = 4 , проходимой в положительном направлении;
в) ( y2 − z2 )dx + 2 yzdy − x2 dz вдоль кривой x = t, y = t2 , z = t3 , t [0;1],
проходимой в направлении возрастания параметра t . |
G |
G |
G |
||
1.8. Вычислить работу векторного поля F(M ) = y i |
− x i вдоль кривой |
|
AB : дуга окружности x2 + y2 =1 с концевыми точками A(−1 / 2;−1 / 2)
и B(1 / 2;1 / 2) , |
причем движение от A к B соответствует |
||
отрицательному направлению на окружности. |
|||
|
|
|
G |
1.9. Найти циркуляцию векторного поля F(M ) вдоль замкнутого контура |
|||
L при обходе его в положительном направлении, если: |
|||
JG |
|
G |
G |
а) F(M ) = (x |
− y) i |
+ (2x + y) j , L: треугольник с вершинами A(1;1), |
|
B(3;3) и C(3; −1) ; |
G |
G |
|
JG |
|
||
б) F(M ) = (x |
+ y) i |
+ ( y − x) j, L: эллипс 4x2 +9 y2 = 36 . |
|
1.10. С помощью формулы Грина вычислить криволинейные интегралы второго рода от следующих подынтегральных выражений (указанные контуры обходятся в положительном направлении):
а) xy2 dy − x2 dx, L: окружностьx2 + y2 |
= a2 ; |
||||
б) (x + y)dx −(x − y)dy , L: эллипс |
x2 |
+ |
|
y2 |
=1. |
a2 |
|
a2 |
|||
|
|
|
|
||
1.11. С помощью криволинейного интеграла найти функцию u(x, y) , если:
50
