
Ми10 крив и пов
.pdf
При пересечении гиперболического параболоида плоскостью z = h (h ≠ 0), получим гиперболу:
|
|
|
x = h; |
|
||
|
|
|
|
|
|
|
|
2 |
|
2 |
|
||
|
x |
|
− |
y |
|
=1. |
2 |
h |
2 |
h |
|||
a |
|
b |
|
|||
При различных значениях h получается семейство гипербол, лежащих в плоскостях, параллельных плоскости х0у. Вершины гипербол для h > 0
лежат на параболе (2.8* ) , а для h < 0 – на параболе (2.8** ) . При h = 0 гиперболы вырождаются в пару прямых, лежащих в плоскости х0у:
|
|
z = 0; |
|
|
z = 0; |
|
||||||
|
|
|
y2 |
|
|
|
b |
|
||||
x |
2 |
|
|
|
|
|||||||
|
|
|
− |
|
|
= 0, |
|
y = ± |
|
|
x. |
|
|
|
|
|
a |
||||||||
|
2 |
b |
2 |
|
||||||||
a |
|
|
|
|
|
|
|
|
||||
Из всего вышеизложенного заключаем, что гиперболический параболоид – поверхность, изображенная на рис. 2.5, по виду напоминающая «седло».
6. Коническая поверхность
Каноническое уравнение: x2 + y2 = z2 . a2 b2 c2
Все координатные плоскости являются плоскостями симметрии этой поверхности. Сечение конической поверхности плоскостью z = h (при h ≠
|
z = h; |
|
|
ah |
|
|
bh |
|
|||
0) – эллипс x2 |
|
y2 |
с полуосями a1 |
= |
и b1 |
= |
. Плоскость z = 0 |
||||
|
|
|
|||||||||
|
|
+ |
|
=1, |
|
|
c |
|
|
c |
|
a2 |
b2 |
|
|
|
|||||||
1 |
1 |
|
|
|
|
|
|
|
|
||
(h = 0) пересекает коническую поверхность в единственной точке (0; 0; 0).
При увеличении |h| полуоси эллипса увеличиваются. Если a = b , то полуоси равны, конус называется круговым. При сечении конической поверхности плоскостями х = 0 и у = 0 получаем пары прямых, соответственно: z = ± bc y и z = ± ac x .
61

Рис. 2.6
Таким образом, коническая поверхность состоит из прямых (образующих конуса), проходящих через одну точку, в нашем случае – начало координат (вершину конуса), и имеет вид, представленный на рис. 2.6.
Цилиндрические поверхности
Уравнения цилиндрических поверхностей накладывают связь только на две координаты, а третья отсутствует, то есть она может принимать любые значения. На плоскости х0у уравнение вида F(х, у) = 0 определяет некоторую линию L – направляющую цилиндрической поверхности. Пусть точка М0(х0, у0, z0) лежит на поверхности, тогда при любых z точки с координатами (х0, у0, z) также лежат на этой поверхности. Все точки с координатами такого вида образуют прямую, проходящую через М0 параллельно оси 0z. Все такие прямые называют образующими цилиндрической поверхности. Все сечения, параллельные плоскости х0у, будут повторять направляющую, то есть для эллиптического цилиндра –
|
|
2 |
|
2 |
|
|
|
эллипс |
|
x |
|
+ |
y |
=1 |
, для гиперболического цилиндра – гиперболу |
|
2 |
2 |
|||||
|
a |
|
|
b |
|
|
|
Рис. 2.7
62

|
2 |
|
2 |
|
|
|
|
|
x |
|
− |
y |
=1 |
, для параболического цилиндра – параболу |
( y2 = 2 px). |
|
2 |
2 |
|||||
a |
|
|
b |
|
|
|
|
Эллиптический цилиндр: x2 + y2 =1 (рис. 2.7); a2 b2
гиперболический цилиндр: x2 − y2 =1 (рис. 1.8); a2 b2
Рис. 2.8
параболический цилиндр: y2 = 2 px (рис. 2.9).
Рис. 2.9
Замечание. Если в уравнении поверхности отсутствует одна из декартовых координат, то есть, например, уравнение поверхности имеет вид F(у, z) = 0, то это цилиндрическая поверхность с образующими, параллельными координатной оси отсутствующей координаты (в нашем случае оси 0х). Направляющая этой цилиндрической
поверхности – кривая, лежащая в плоскости изменения двух других координат, присутствующих в уравнении поверхности( то есть кривая, лежащая в плоскости у0z, имеющая уравнение F(у, z) = 0).
Поверхности вращения Определение. Поверхностью вращения называется поверхность,
образованная вращением какой-либо плоской линии вокруг прямой, лежащей в плоскости этой линии.
63
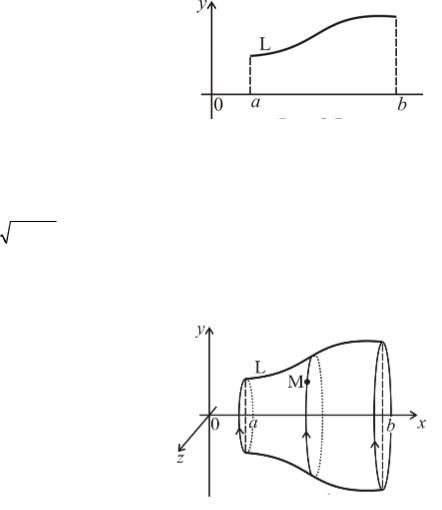
Чаще всего ось вращения принимают за одну из координатных осей. Пусть некоторая кривая L лежит в плоскости х0у (рис. 2.9) и имеет уравнение y = f(x), х [а; b].
Рис. 2.9
Найдем уравнение поверхности, которая получится вращением кривой L вокруг оси Ox (рис. 2.9). Очевидно, точка M с координатами (х; у; z), где х[а; b], принадлежит искомой поверхности тогда и только тогда, когда
y2 + z2 =| f (x) | . Действительно, точки с координатами (х; у; z) и (х; f(x); z)
лежат на одной окружности с центром в точке (х; 0; 0), значит расстояния от них до центра окружности равны. Таким образом, уравнение
Рис. 2.10
поверхности, полученной вращением кривой y = f(x) вокруг оси 0х, имеет вид: y2 + z2 = ( f (x))2 , x [a;b]. Заметим, что последнее уравнение
получается из уравнения линии следующим образом: обе части уравнения линии возводятся в квадрат и y2 заменяется на y2 + z2. В частности, если
кривая L задана в плоскости х0у уравнением y2 = F(x) , то уравнение поверхности, полученной вращением этой кривой вокруг оси 0х (просто заменяем y2 на y2 + z2), имеет вид: y2 + z2 = F(x) . Аналогично для других координатных плоскостей В общем виде уравнения поверхностей
вращения: вокруг оси 0х: F(x, y2 + z2) = 0; вокруг оси 0у: |
F(у, х2 + z2) = 0; |
|||||||||
вокруг оси 0z: F(z, x2 + y2) = 0. |
|
|
|
|
|
|
||||
|
|
Рассмотрим уравнение гиперболы, лежащей в плоскости х0у (рис. 2.11): |
||||||||
|
x2 |
|
y2 |
2 |
|
2 |
|
2 |
|
|
|
|
− |
|
=1.Если в этом уравнении заменить х |
|
на х |
|
+ |
z |
, то получим |
|
a2 |
b2 |
|
|
||||||
64
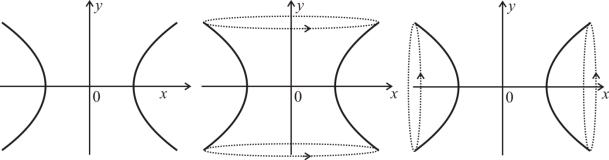
уравнение поверхности вращения вокруг оси 0у: |
x2 |
+ z2 |
− |
y2 |
=1, |
в данном |
|
|
a2 |
b2 |
|||||
|
|
|
|
|
|
||
случае – однополостный |
гиперболоид вращения |
(рис. 2.12). Если |
|||||
рассмотреть вращение этой же гиперболы вокруг оси 0х, то есть в уравнении
заменить переменную у2 на у2 + z2, то получим уравнение двуполостного
гиперболоида вращения (рис. 2.13): |
x2 |
− |
y2 + z2 |
=1. |
|
a2 |
b2 |
||||
|
|
|
Рис.2.11 |
|
Рис.2.12 |
|
|
|
Рис.2.13 |
|||||||
|
x2 |
− |
y2 |
|
=1. |
x2 + z2 |
− |
y2 |
=1, |
x2 |
− |
y2 + z2 |
=1. |
|
a2 |
b2 |
a2 |
b2 |
a2 |
b2 |
|||||||
|
|
|
|
|
|
|
|||||||
Аналогично рассуждая, можно получить частные случаи некоторых поверхностей второго порядка:
Поверхность |
|
|
вокруг оси 0z |
|
|
вокруг оси 0у |
|
|
вокруг оси 0х |
||||||||||||||||||||||||||||
вращения |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
эллипсоид |
|
x |
2 |
+ y |
2 |
|
|
z |
2 |
|
|
x |
2 |
|
+ z |
2 |
|
|
|
|
2 |
|
|
x |
2 |
|
|
y |
2 |
+ |
z |
2 |
|
||||
вращения |
|
|
|
+ |
|
|
=1 |
|
|
|
|
|
|
+ |
|
y |
=1 |
|
|
+ |
|
|
|
|
=1 |
||||||||||||
|
|
|
2 |
|
|
c |
2 |
|
|
|
2 |
|
|
|
|
2 |
|
a |
2 |
|
|
|
2 |
|
|
||||||||||||
|
|
|
|
a |
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|||||
однополостный |
|
x2 + y |
2 |
|
|
z |
2 |
|
|
x2 + z2 |
|
|
y2 |
|
|
y2 + z2 |
|
x |
2 |
|
|||||||||||||||||
гиперболоид |
|
|
|
|
|
|
− |
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
− |
|
|
|
=1 |
|
|
|
|
|
|
|
|
− |
|
|
=1 |
|
|
|
a2 |
|
|
c2 |
|
|
|
a2 |
|
|
|
|
b2 |
|
|
|
b2 |
|
|
a |
2 |
||||||||||||||
вращения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
двуполостный |
|
z |
2 |
|
x |
2 |
+ y |
2 |
|
|
y |
2 |
|
|
x |
2 |
+ z |
2 |
|
|
x |
2 |
|
y |
2 |
+ z |
2 |
|
|||||||||
гиперболоид |
|
|
− |
|
|
=1 |
|
|
|
− |
|
|
|
=1 |
|
|
− |
|
|
|
=1 |
||||||||||||||||
|
c2 |
|
|
a2 |
|
|
|
b2 |
|
|
|
|
a2 |
|
|
|
a2 |
|
|
|
b2 |
|
|
||||||||||||||
вращения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
параболоид |
|
x |
2 |
+ y |
2 |
= 2z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
вращения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из вышеизложенного можно вывести еще один способ «узнавания» и построения поверхностей второго порядка. Пусть, для наглядности, требуется определить тип поверхности x2 + z2 – y + 1 = 0.
1. Находим в уравнении поверхности суму квадратов каких-то двух переменных, в нашем случае это переменные х2 + z2, значит можно утверждать, что данная поверхность получена вращением вокруг оси 0у.
65

2.Закрываем мысленно одну из этих переменных, например z2, тогда получаем уравнение параболы: x2 – y + 1 = 0.
3.Строим эту параболу, представляем поверхность, которая получится при вращении ее вокруг оси 0у − параболоид вращения.
Если в уравнении изменить коэффициенты при переменных х и z, например,
3x2 + 2z2 – y + 1 = 0, то это уже эллиптический параболоид.
Пример 2.2. Назвать и схематично изобразить следующие поверхности:
1) |
x2 |
+ |
y2 |
+ |
|
z2 |
=1; |
2) |
x2 |
+ |
y2 |
− |
z2 |
=1; 3) |
z = |
|
x2 |
+ |
y2 |
;4) x |
2 |
+ y |
2 |
=1; |
|||||
9 |
64 |
16 |
4 |
36 |
25 |
|
|
1 |
4 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
5) |
y2 |
|
+ z2 =1; 6) |
y2 |
= 4x; 7) z2 = 4x; 8) x2 |
+ |
z2 |
|
= y2 ; 9) x2 − y2 |
= 0; |
|||||||||||||||||||
4 |
|
4 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
||||
10) x2 + 2x + y2 − 4 y + z +9 = 0.
Решение. 1) Это каноническое уравнение эллипсоида (см. рис. 2.1) с полуосями а = 3, b = 8, с = 4.
2) Это уравнение однополостного гиперболоида (см. рис. 2.2), у которого а = 2, b = 6, с = 5.
3) Это уравнение эллиптического параболоида (см. рис. 2.4). Пересечем эллиптический параболоид плоскостью z = 1, параллельной
66
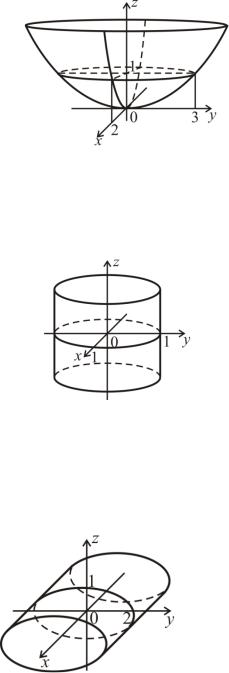
координатной плоскости х0у, в сечении получим эллипс, у которого а =
|
|
|
z =1; |
|
||||
1, b = 2: |
|
2 |
|
|
2 |
|
|
|
|
|
y |
|
|
||||
|
|
x |
|
+ |
|
|
=1. |
|
|
|
|
|
|
|
|||
|
1 |
4 |
|
|
||||
4) В уравнении отсутствует декартовая координата z, следовательно (см. рис. 2.7), это уравнение цилиндрической поверхности с образующими, параллельными оси 0z. Направляющая этой цилиндрической поверхности – окружность, лежащая в плоскости х0у, имеющая уравнение x2 + y2 =1
Это круговой цилиндр
5) В уравнении отсутствует декартовая координата х, следовательно (см. рис. 2.7), это уравнение цилиндрической поверхности с образующими, параллельными оси 0х. Направляющая этой цилиндрической поверхности
– эллипс, лежащий в плоскости у0z, имеющий уравнение: |
y2 |
+ z2 =1. |
|
4 |
|||
|
|
Это эллиптический цилиндр
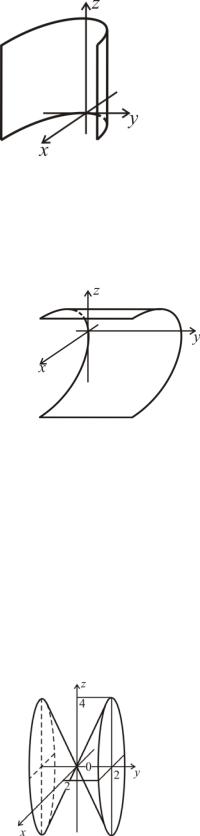
6) В уравнении отсутствует декартовая координата z, следовательно
(см. рис. 2.7), это уравнение цилиндрической поверхности с образующими, параллельными оси 0z. Направляющая – парабола, лежащая
в плоскости х0y, имеющая уравнение: y2 = 4x.
67
.
Это параболический цилиндр
7) В уравнении отсутствует декартовая координата у, следовательно (см. рис .2.7), это уравнение цилиндрической поверхности с образующими,
параллельными оси 0y.Направляющая – парабола, лежащая в плоскости x0z, имеющая уравнение: z2 = 4x.
Это параболический цилиндр |
|
|
|
|
|
|
||
8) Если коническая поверхность имеет уравнение: |
x2 |
+ |
y2 |
= |
z2 |
, |
то внутри |
|
a2 |
b2 |
c2 |
||||||
|
|
|
|
|
||||
полостей этой поверхности проходит ось 0z (см. рис. 2.6). Тогда в нашем случае внутри полостей конической поверхности проходит ось 0y. Сечения данной поверхности плоскостями y = h – эллипсы:
|
|
y = h; |
|
|
|
y = h; |
|
||||
|
|
|
z2 |
|
|
|
|
|
z2 |
с полуосями а1 = h, b1 = 2h. |
|
|
2 |
|
|
2 |
, x2 |
2 |
|
||||
x |
|
+ |
|
= h |
|
|
|
|
+ |
|
=1, |
|
4 |
|
|
|
|||||||
|
|
|
|
4h2 |
|||||||
|
|
|
|
|
h2 |
|
|
|
|||
Например, при h = 2: полуоси а1 = 2, b1 = 4.
9) В уравнении отсутствует декартовая координата z, следовательно (см. рис. 2.7), это уравнение цилиндрической поверхности с образующими,
68
параллельными оси 0z. Направляющая – линия, лежащая в плоскости х0у:
х2 − у2 = 0 х2 = у2 х= ± у.
Если направляющими являются две прямые, то поверхность вырождается в пару плоскостей, проходящих через ось 0z.
10)Предварительно выделяем полные квадраты при переменных х и у:
x2 + 2x + y2 − 4 y + z +9 = 0; (x2 + 2x +1) −1 + ( y2 − 4 y + 4) − 4 + z +9 = 0;
(x +1)2 + ( y − 2)2 = −(z − 4).
Это уравнение эллиптического параболоида с вершиной в точке (−1; 2; 4). При пересечении его плоскостью z = 0, получим окружность с центром в точке (−1; 2) и радиусом 2.
2.2. Поверхностный интеграл первого рода. Теорема существования интеграла
Поверхностный интеграл первого рода представляет собой обобщение естественное обобщение двойного интеграла, каким криволинейный интеграл первого рода является по отношению к определенному интегралу.
Пусть на некоторой двусторонней гладкой (или кусочно гладкой) поверхности Q , ограниченной кусочно гладким контуром L, определена
функция |
f (M ) = f (x.y, z) . Выберем |
разбиение |
поверхности |
Q на |
конечное число частичных областей qi , i =1, 2,..., n, с площадями |
∆qi . В |
|||
каждой |
частичной области qi |
возьмем |
произвольную |
точку |
69
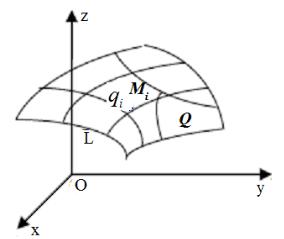
Mi (xi , yi , z1 ) qi (рис.2.2.1). Пусть |
d — максимальный из диаметров di |
частичных областей qi ,i =1, 2,..., n. |
Сумму |
n |
|
∑ f (xi , yi , zi )∆qi |
(2.9) |
i=1
Рис.2.2.1
назовем интегральной суммой для функции f (x.y, z) по поверхности Q .
Если при стремлении d к нулю, существует конечный предел
интегральных сумм (2.9), который не зависит от способа разбиения поверхности Q на части qi и от выбора точек Mi qi , то его называют
поверхностным интегралом первого рода от функции
f (M ) = f (x.y, z) по поверхности Q или интегралом по площади поверхности Q и обозначают ∫∫ f (x, y, z)dq . Итак, по определению
Q |
|
|
|
n |
|
∫∫ f (x, y, z)dq = limd →0 |
∑ f (xi , yi , zi )∆qi . |
(2.10) |
Q |
i=1 |
|
( dq – дифференциал площади поверхности).
|
Из определения |
поверхностного интеграла первого рода следует, что |
||||
он не зависит от выбора стороны поверхности. |
f (x, y, z) ≡1, |
то есть, |
||||
В |
частности, если |
в |
равенстве |
(2.10) функция |
||
|
n |
|
|
|
|
|
∫∫dq = limd →0 ∑∆qi , то |
получается |
формула для |
вычисления |
площади |
||
Q |
i=1 |
|
|
|
|
|
поверхности SQ : |
|
|
|
|
|
|
|
|
|
SQ = ∫∫dq. |
|
(2.10*) |
|
|
|
|
|
Q |
|
|
Теорема 2.1. (Теорема существования поверхностного интеграла первого рода)
70
