Ми10 крив и пов

поверхность Q . Векторное поле будем трактовать как поле скоростей

течения жидкости. В этом случае положительное значение потока векторного поля через замкнутую поверхность Q означает, что из области,

ограниченной поверхностью Q , вытекает жидкости больше, чем в нее

втекает. Значит, в области имеются точки или подобласти, в которых жидкость образуется (например, происходит образование воды при таянии снега или льда). Точки такого рода называют источниками векторного поля. Аналогично отрицательное значение потока через поверхность Q

означает, что в область втекает жидкости больше, чем из нее вытекает.

Рис.2.3.10

Значит, в области есть точки, в которых жидкость исчезает (например, испаряется или замерзает). Такие точки называют стоками векторного

поля.

Источники и стоки могут быть точечными или распределенными. На наличие точечных источников в области указывают векторные линии, начинающиеся в области, а на наличие точечных стоков – векторные линии, заканчивающиеся в области. На рис. 2.3.10 точка M1

возникновения векторных линий является источником, а точка M2 окончания векторных линий стоком.

91

Точечный источник или сток характеризуют интенсивностью, равной объему жидкости, которая возникает или исчезает в этой точке в единицу времени, а распределенные источники и стоки – плотностью интенсивности, т.е. количеством жидкости, возникающей или исчезающей в единице объема в единицу времени. Интенсивность стоков удобно считать отрицательной, полагая, что сток – это источник отрицательной интенсивности. Тогда поток PQ векторного поля скоростей

через поверхность Q получает естественную интерпретацию как

суммарная интенсивность всех источников и стоков в области, ограниченной этой поверхностью. Понятия источника (стока) и его интенсивности в задачах различного физического содержания приобретают различный смысл. Так, в случае векторного поля электрической напряженности роль источников (стоков) играют положительные (отрицательные) заряды, а их интенсивность измеряется величиной этих зарядов. Если же векторное поле описывает тепловой поток, то источники и стоки характеризуют выделение и поглощение теплоты, причем интенсивность источника (стока) представляет собой количество теплоты, выделяемой (поглощаемой) в единицу времени.

Остановимся на случае распределенных источников векторного поля. Такие источники могут быть распределены по некоторой области пространства, по некоторой поверхности или линии. Если источники распределены по области Ω, ограниченной замкнутой поверхностью Q ,

то отношение потока PQ векторного поля через поверхность Q к объему VΩ области Ω есть средняя плотность источников векторного поля в

области

Ω. Зафиксировав некоторую точку M , полагая, что область Ω содержит M , перейдем к пределу при dΩ → 0 ( dΩ – диаметр области Ω):

Если этот предел существует, то его значение определяет интенсивность распределенного источника векторного поля в точке M . Отметим, что этот предел аналогичен пределу, определяющему плотность вещества в точке .

Предел (2.32), если он существует, называют дивергенцией (иногда

пространственной области Ω, и обозначают через divF(M ) . Доказано(см.

JG

например [2]), что divF(M ) определяется равенством:

92

Символ div образован из первых букв латинского слова divergentia – расхождение. Этот символ, как и сам термин „дивергенция", ввел в 1878 г. У.К. Клиффорд.

Дивергенция diva векторного поля a а в точке М есть скаляр

divF(M ) . Обратим внимание на то, что градиент gradu скалярногоJGполя u = u(x, y, z) есть векторное поле, в то время как дивергенция divF(M ) векторного поля a есть скалярное поле.

2.3.7. Формула Стокса

Формула Стокса обобщает формулу Грина на случай пространственной кривой. Она устанавливает связь между поверхностным интегралом по поверхности Ω и криволинейным интегралом II-го рода по границе L этой поверхности.

Пусть гладкая двусторонняя поверхность Q ограничена замкнутым

гладким контуром L, лежащим на выбранной стороне двусторонней поверхности (рис.2.3.11). Зададим на этом контуре положительное направление обхода по следующему правилу. Будем считать, что наблюдатель, находящийся на выбранной стороне поверхности (это означает, что нормаль к поверхности направлена от его ног к голове) движется по контуру в положительном направлении, если он движется против часовой стрелки, т.е. область, ограниченная контуром, остается от него слева (рис.2.3.11). Отметим, что для замкнутой (т.е. не имеющей границы) поверхности (например, сферы) сформулированное выше правило не работает: в этом случае любой замкнутый контур ограничивает сразу две области (экватор Земли, например, ограничивает и северное полушарие, и южное). В подобных случаях для задания положительного направления на контуре приходится оговаривать, границей какой именно области будет считаться этот контур.

С учетом сделанного уточнения, можно сказать, что, если на двусторонней поверхности выбрана определенная сторона, то положительное направление на любом замкнутом контуре определяется однозначно. Легко видеть, что верно и обратное: если для некоторого замкнутого контура на поверхности выбрано положительное направление обхода, то тем самым задана сторона поверхности.

Замечание. Если на двусторонней поверхности выбрана определенная сторона (определяющая положительное направление обхода по

93

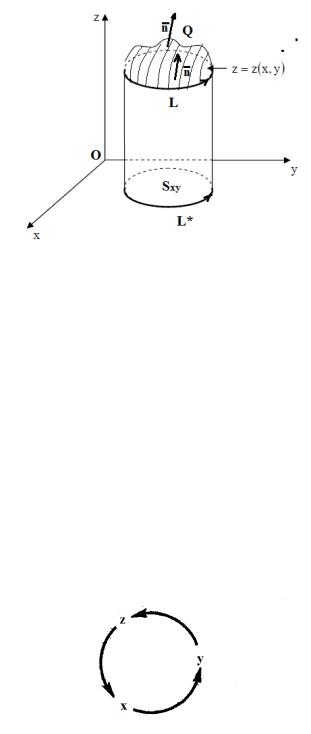
замкнутому контуру, лежащему на поверхности), или же задано положительное направление обхода по замкнутому контуру, лежащему на поверхности (и, тем самым, определена сторона поверхности), то говорят, что на поверхности задана ориентация.

Рис.2.3.11

Теорема 2.4. (Формула Стокса)

Пусть в некоторой пространственной области G , целиком содержащей

где обход контура L при выбранной стороне поверхности Q происходит

в положительном направлении (Доказательство теоремы см,

например,[1]).

Мнемоническое правило. Чтобы запомнить левую часть этой формулы, можно поступить следующим образом. Изобразим переменные x, y и z в виде круговой диаграммы (рис.2.3.12).

Рис.2.3.12

Начинаем с x и, продвинувшись до y , берем функцию Y(x, y, z) , дифференцируем ее по x и вычитаем частную производную X (x, y, z) по y (занятые в этом члене дифференциалы dxdy от тех же переменных).

94

Теперь начинаем от y . Продвинувшись до z , берем функцию Z(x, y, z) и

дифференцируем ее по y . Так как первый член ∂∂Zy , то второй будет ∂∂Yz

со знаком минус (занятые в этом члене дифференциалы dydz ). Затем

начинаем от z и т. д.

Замечание 1. Если поверхность Q есть область на плоскости xOy (z = 0) , то проекции Q на плоскости xOz и yOz имеют нулевую площадь, и

поэтому в левой части формулы Стокса (2.33) останется лишь первый член. Так как dz = 0 , то в правой части этой формулы будет отсутствовать последнее слагаемое. Формула примет следующий вид:

– это есть формула Грина. Таким образом, формула Грина – частный случай формулы Стокса.

Замечание 2. Как и формула Грина, формула Стокса обобщается на случай, когда поверхность ограничена несколькими кусочно-гладкими контурами. При этом в левой части равенства (2.33) появляется сумма криволинейных интегралов по граничным контурам, проходимым в положительном направлении, т.е. так, что при обходе каждого контура поверхность остается слева, если смотреть с конца выбранного вектора нормали к поверхности.

Замечание 3. На основании формулы (2.23), формулу Стокса можно записать и так:

где α – угол между вектором n и осью Ox , β – угол между вектором n и осью Oy , γ — угол между вектором n и осью Oz .

Замечание 4. Пусть задано векторное поле

JG G G G

F(M ) = X (x, y, z) i + Y(x, y, z) j + Z(x, y, z) k ,

координаты которого удовлетворяют условиям теоремы 2.4.. Вектор

95

То есть, формулу Стокса, в терминах векторного поля, можно сформулировать следующим образомG .

Циркуляция векторного поля F(M ) вдоль замкнутого контура L,

обходимого в положительном направлении, равна потоку ротора векторного поля через поверхность Q , натянутую на этот контур.

Пример 2.8. Вычислить двумя способами (непосредственным подсчетом криволинейного интеграла второго рода и по формуле Стокса)

криволинейный интеграл I = >∫ ydx + z2 dy + x2 dz, где L – окружность, по

L

которой плоскость z = 3 пересекает сферу, заданную уравнением x2 + y2 + z2 = 4 (рис.2.3.13).

96

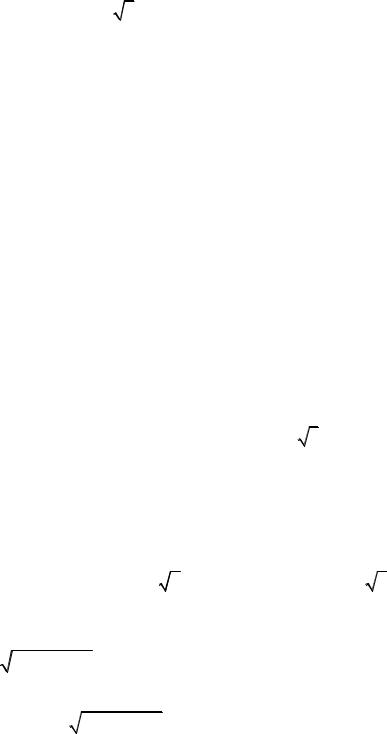
криволинейный интеграл епосредственно, составим параметрические уравнения окружности L :

x = cost;

y = sin t; t [0;2π].

z = 3,

Из параметрических уравнений находим dx = −sin tdt, dy = costdt и dz = 0 .

Используя формулу (1.23) для вычисления криволинейного интеграла, получим

Чтобы вычислить криволинейный интеграл с помощью формулы Стокса,

положим X (x, y, z) = y, Y(x, y, z) = z2 , Z(x, y, z) = x2 . Тогда

∂∂Yx − ∂∂Xy = −1, ∂∂Zy − ∂∂Yz = −2z, ∂∂Xz − ∂∂Zx = −2z.

Согласно формуле Стокса (2.33), рассматриваемый криволинейный интеграл сводится к поверхностному интегралу

контуром L (рис.2.3.13).

Сначала вычислим поверхностный интеграл по верхнему сегменту сферы Q1 . Чтобы направление обхода контура L было положительным, на

сегменте сферы следует выбрать верхнюю сторону. Проекциями сегмента

входящего в (2.36) поверхностного интеграла второго рода ∫∫2xdxdz

Q

получаем

97

∫∫2xdxdz = ∫∫2xdxdz = 2∫∫xdxdz − 2∫∫xdxdz = 0.

Q Q1 Sxz Sxz

Аналогично для области Syz имеем

∫∫2zdydz = ∫∫2zdydz = 2∫∫zdydz − 2∫∫zdydz = 0.

Q Q1 Sxz Sxz

Так как угол γ между единичным вектором нормали n и осью Oz острый, то есть cosγ ≥ 0 (рис.2.3.13) для выбранной стороны сегмента сферы,

находим

∫∫dxdy =∫∫dxdy = ∫∫dxdy =π,

Q Q1 Sxy

поскольку область Sxy есть круг радиуса 1 с площадью π . Подставляя

найденные результаты в (2.36), получим I = −π.

Теперь вычислим поверхностный интеграл (2.36) по поверхности Q2 –

Итак, все три способа вычисления рассматриваемого криволинейного

Рис.2.3.14

Решение. Воспользуемся формулой Стокса (2.35). В качестве поверхности Q с границей L примем часть параболоида

98

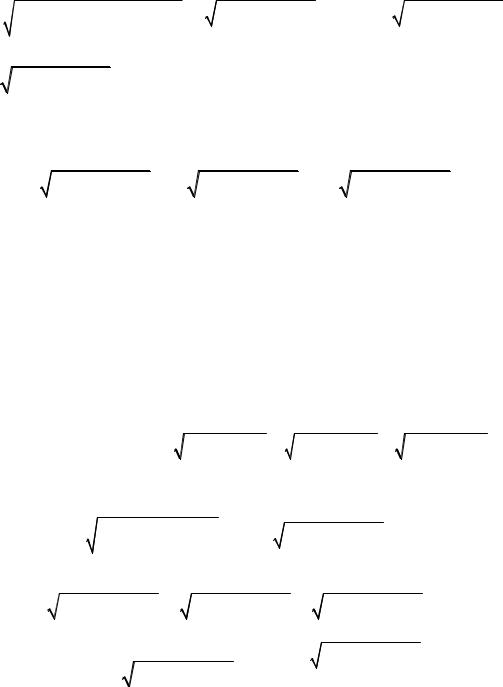
u(x, y, z) = z − z(x, y) = z −1 + x2 + y2 = 0, x ≥ 0, y ≥ 0, z ≥ 0, лежащую в

первом октанте. Положительным направлением обхода контура будем считать движение против часовой стрелки, если смотреть со стороны

Sxy

99

где Sxy :x2 + y2 ≤1, x ≥0, y ≥0 – проекция поверхности Ω на плоскость xOy .

Для вычисления двойного интеграла перейдем в полярную систему координат