
Ми10 крив и пов
.pdfПогрешность этого приближенного равенства тем меньше, чем мельче разбиение кривой AB на элементарные дуги. Поэтому естественно за
n
массу кривой AB принять значение предела m = lim ∑ρ(Mi )∆si , где
λ→0 i=1
λ = max ∆si — наибольшая из длин ∆si элементарных дуг.
i=1,...,n
Сравнивая данное определение массы кривой с определением криволинейного интеграла первого рода, получим
m = ∫ ρ(M )ds = ∫ ρ(x, y.z)ds.
AB |
AB |
Моменты инерции, статические моменты материальной кривой и координаты ее центра масс.
Моменты инерции для материальной кривой вводят так же, как и для неоднородного тела или пластины. Пусть для материальной пространственной кривой AB задана ее линейная плотность ρ(x, y, z) .
Разделим кривую AB точкамиA0 = A, A1 ,..., An = B на элементарные дуги Ai−1 Ai ,i =1,..., n, с длинами ∆si . Будем предполагать, что это разбиение
настолько мелкое, что плотность в пределах одной элементарной дуги можно приближенно считать постоянной. В этом случае каждую элементарную дугу Ai−1 Ai можно заменить материальной точкой
Mi (xi , yi , zi ) Ai−1 Ai , в которой сосредоточена вся масса ρ(xi , yi , zi )∆si этой дуги (см. рис. 1.2.1). Суммируя массы по всем элементарным дугам, для материальной кривой ABможем приближенно принять, что:
n
момент инерции относительно оси Oz JOz ≈ ∑(xi2 + yi2 )ρ(xi , yi , zi )∆si ;
i=1
n
момент инерции относительно плоскости yOz JyOz ≈ ∑xi2 ρ(xi , yi , zi )∆si ;
i=1
n
момент инерции относительно плоскости xOz JxOz ≈ ∑yi2 ρ(xi , yi , zi )∆si .
i=1
В качестве точного значения этих моментов инерции естественно
взять предел правых частей равенств при λ = max ∆si → 0 . Это приводит к
i=1,...,n
записи моментов инерции через криволинейные интегралы
JOz = ∫ (x2 + y2 )ρ(x, y, z)ds; JyOz = ∫ x2 ρ(x, y, z)ds;
AB |
AB |
|
JxOz |
= ∫ y2 ρ(x, y, z)ds. |
(1.3) |
|
AB |
|
21
Аналогичным образом можно получить выражения для моментов инерции кривой относительно координатных осей Ox , Oy и координатной
плоскости xOy . |
|
|
|
|
Для плоской кривой АВ в координатной плоскости |
xOy с линейной |
|||
плотностьюρ(x, y) момент |
инерции |
JOz относительно |
оси |
Oz обычно |
называют полярным моментом инерции и обозначают |
JO . |
Моменты |
||
инерции относительно осей |
Oy и |
Ox совпадают с моментами инерции |
||
относительно плоскостей xOz и yOz , и их обозначают через Jy и Jx . Формулы для статических моментов материальной кривой Sx , Sy , Sz
относительно, соответственно, плоскостей yOz , xOz , xOy |
можно |
получить, проводя те же рассуждения, в которых кривая заменяется системой конечного числа материальных точек, а затем выполняется переход к пределу. Эти формулы имеют следующий вид:
Sx = ∫ xρ(x, y, z)ds; |
Sy = ∫ yρ(x, y, z)ds; Sz = ∫ zρ(x, y, z)ds. |
(1.4) |
||||||||||||||
AB |
|
|
|
AB |
|
|
|
|
|
|
|
|
|
AB |
|
|
Тогда координаты центра масс материальной кривой определятся |
|
|||||||||||||||
следующим образом: |
|
S |
|
|
|
|
Sy |
|
|
|
|
S |
|
|
|
|
x |
= |
x |
; |
y |
= |
; z |
|
= |
z |
. |
|
(1.5) |
||||
|
|
m |
c |
|
|
|
||||||||||
c |
|
m |
c |
|
|
|
m |
|
|
|||||||
В случае плоской кривой |
AB , лежащей в координатной плоскости |
xOy , |
||||||||||||||
статический момент Sz равен нулю и |
zc = 0 , а в формулах |
(1.4), |
для |
|||||||||||||
статических моментов Sx , Sy , |
|
|
|
|
|
|
|
|
|
|
|
|
||||
линейная плотность ρ(x, y) |
не будет зависеть от координаты |
z . В этом |
||||||||||||||
случае Sx и Sy часто называют статическими моментами относительно осей Oy и Ox .
1.1.4. Вычисление криволинейного интеграла первого рода |
|
|
Пусть кривая AB задана параметрическими уравнениями |
|
|
x = x(t); |
|
|
|
t [α; β], |
(1.5) |
y = y(t); |
||
|
|
|
z = z(t), |
|
|
где функции x(t), y(t) и z(t) непрерывны вместе со своими производными на отрезке [α; β]. Тогда кривая AB спрямляема и для нее определен натуральный параметр s . Натуральный параметр можно отсчитывать от любого конца кривой и в данном случае отсчет удобно вести от начальной точки кривой, соответствующей значению t =α. Тогда возрастанию параметра t будет соответствовать возрастание параметра s, а для
дифференциала длины дуги кривой будет выполняться равенство
22
|
ds = (x' (t))2 + ( y' (t))2 + (z' (t))2 dt. |
|
(1.6) |
При этом |
значение t =α соответствует точке A и |
значению |
s = 0 , а |
значение t = β — точке B и значению s = sAB . Следовательно, имеем: |
|||
|
β |
|
|
∫ f (x, y, z)ds = ∫ f (x(t), y(t), z(t)) (x' (t))2 + ( y' (t))2 |
+ (z' (t))2 dt. |
(1.7) |
|
AB |
α |
|
|
Таким образом, для вычисления криволинейного интеграла первого рода следует заменить в подынтегральной функции переменные x, y, z их
выражениями через параметр t , а дифференциал ds — дифференциалом длины дуги, выразив его через параметр t. Оговоренное выше согласование параметра t и натурального параметра s означает, что в определенном интеграле в (1.7) справа нижний предел интегрирования меньше верхнего, то есть α < β .
|
|
|
|
x = x(t); |
t [α; β], при тех же |
||
Если криваяAB задана на плоскости |
|
||||||
|
|
|
|
y = y(t), |
|
|
|
ограничениях на функции x(t), y(t) , то формула (1.7) запишется |
|
||||||
следующим образом: |
|
|
|
|
|
||
|
|
β |
|
|
|
|
|
|
∫ f (x, y)ds = ∫ f (x(t), y(t)) (x' (t))2 + ( y' (t))2 dt. |
(1.8) |
|||||
|
AB |
α |
|
|
|
|
y = y(x) , |
Если |
плоская |
кривая АВ |
является |
графиком функции |
|||
x [a;b], |
то в качестве параметра кривой естественно выбрать абсциссу x |
||||||
точки кривой. При этом формула (1.8) приобретает вид |
|
||||||
|
∫ |
f (x, y)ds = ∫b |
f (x, y(x)) |
1 + ( y' (x))2 dx. |
(1.9) |
||
|
AB |
|
a |
|
|
|
|
Аналогично при задании кривой функцией в виде x = x( y), y [c;d], |
|||||||
получаем |
∫ f (x, y)ds = ∫b |
|
|
|
|
|
|
|
f (x( y), y) 1 + (x' ( y))2 dy. |
(1.10) |
|||||
|
AB |
a |
|
|
|
|
|
Пусть кривая АВ задана в полярной системе координат уравнением r = r(ϕ), ϕ [ϕ1;ϕ2 ] . Тогда, учитывая формулы x = r cosϕ и y = rsinϕ связи декартовых и полярных координат, а также выражение для
дифференциала |
длины |
дуги |
в |
полярных |
координатах |
ds = r2 + r'2 dϕ, находим |
|
|
|
|
|
|
ϕ2 |
|
|
|
|
∫ f (x, y)ds = ∫ f (r cosϕ, r sinϕ) |
r(ϕ)2 + r(ϕ)'2 dϕ. |
(1.11) |
|||
AB |
ϕ1 |
|
|
|
|
23
Пример 1.5. Вычислить криволинейный интеграл первого рода ∫ xyzds
вдоль пространственной кривой |
AB, |
|
AB |
|
заданной |
параметрическими |
|||
уравнениями |
|
|
|
|
|
x = t; |
|
|
|
|
y = t2 / 2; t |
[0;1]. |
|
|
|
|
|||
|
|
/ 3, |
|
|
z = 8t3 |
|
|
||
Решение. Предварительно находим
ds = |
(x' (t))2 + ( y' (t))2 |
+ (z' (t))2 dt = 1 + t2 |
+ 2tdt = (1+ t)dt. |
||||||
Далее в соответствии с формулой (1.7) получаем |
|
|
|||||||
|
|
∫ xyzds = |
|
2 |
∫1 t9/ 2 (1 +t)dt = |
16 |
|
2. |
|
|
|
|
|
|
|
||||
Пример |
1.6. |
AB |
3 |
0 |
143 |
|
|||
Найти положение |
центра |
масс полуокружности |
|||||||
L :x2 + y2 |
= a2 , |
x ≥ 0, с постоянной линейной плотностью ρ. |
|||||||
Решение. Ясно, что центр масс полуокружности в силу симметрии
расположен на оси Ox , т.е. |
yc = 0. |
Для вычисления второй координаты |
||||
центра масс используем параметрическое представление полуокружности |
||||||
в виде |
|
|
|
|
|
|
x = acost; |
t [− |
π |
; |
π |
]. |
|
|
= asin t, |
2 |
2 |
|||
y |
|
|
|
|||
Тогда |
ds = |
(x' (t))2 + ( y' (t))2 dt = |
a2 sin2 t + a2 cos2 tdt = adt, |
и для |
||||||||||||
статического момента |
Sx |
относительно оси Oy (формула 1.4) |
получаем |
|||||||||||||
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sx = ∫xρds = ∫2 |
acost ρadt = 2ρa2 . Масса m полуокружности постоянной |
|||||||||||||||
L |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
линейной плотности ρ пропорциональна ее длине и равна πρa. |
Поэтому |
|||||||||||||||
(формула |
1.5) |
x |
= |
|
S |
x |
|
= |
2ρa2 |
= |
2a |
. |
Итак, центр масс полуокружности |
|||
|
|
|
|
|
|
|
||||||||||
|
|
c |
|
|
m |
|
|
πρa |
|
π |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
расположен в точке |
|
2a |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
;0 . |
|
|
|
|
|
||||||
|
π |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 1.7. Вычислим криволинейный интеграл первого рода от функции f (x, y) = x4/3 + y4/3 вдоль замкнутой кривой L, заданной уравнением x2/3 + y2/3 = a2/3 (астроиды) (см. раздел 1.1).
24
Решение. Для вычисления интеграла запишем кривую в параметрической форме:
|
|
3 |
|
|
|
|
|
|
|
|
x = acos t; t [0;2π). |
|
||
|
y = asin3 t, |
|
||
Находим |
x' (t) = −3acos2 t sin t, |
|
y' (t) = 3asin2 t cost . |
Следовательно, |
(x' (t))2 + ( y' (t))2 = 9a2 cos2 t sin2 t. |
Отметим, что правая |
часть последнего |
||
равенства обращается в нуль в четырех точках, соответствующих
значениям t = 0, t = |
π |
, t =π, t = |
3π |
, т.е. астроида является кусочно- |
|
2 |
2 |
||||
|
|
|
гладкой кривой. Переходя от криволинейного интеграла к определенному, получаем
∫(x4/3 + y4/3 )ds = |
2∫π a4/3 (cos4 t +sin4 t)3a |
|
cost sin t |
|
dt. Функция под знаком |
|
|
||||
|
|
||||
L |
0 |
|
|
|
|
пределенного интеграла справа является периодической с периодом |
π . |
||||||
|
|
|
|
|
|
|
2 |
Поэтому интеграл по отрезку |
[0;2π] можно заменить учетверенным |
||||||
интегралом по отрезку [0; π ]. Таким образом, |
|
||||||
|
2 |
|
|
|
|
|
|
|
|
∫(x4/3 + y4/3 )ds =12a7/3 π∫/ 2 |
(cos5 t sin t +sin5 t cost)dt = |
|
|||
|
|
L |
0 |
|
|
|
|
|
|
= 2a7/3 (−cos6 t +sin6 t) |π / 2 = 4a7/3 . |
|
||||
|
|
|
|
0 |
|
||
Пример 1.8. Вычислим криволинейный интеграл первого рода |
|
||||||
∫ |
y |
ds, где AB — дуга параболы |
y = |
x2 |
, заключенная между точками |
||
|
|
||||||
AB |
x |
|
2 |
|
|
||
A(1;1 / 2) и B(2;2). |
|
|
|
|
|
||
Решение. В данном случае ds = |
1 + y'2 (x)dx = 1 + x2 dx и в соответствии с |
||||||
формулой (1.9) |
|
|
|
|
|
||
∫ |
y |
ds = |
1 |
∫2 x 1 + x2 dx = |
1 |
∫2 |
1+ x2 d(1+ x2 ) = |
1 |
(1+ x2 )3 |
|
2 |
|
|
||||||||||||
|
|
|
|
|||||||||
AB |
x |
2 |
1 |
4 |
1 |
|
6 |
|
|
1 |
||
|
|
|||||||||||
= |
5 5 − |
2 2 |
. |
6 |
|
||
|
|
|
Пример 1.9. Пусть L – правый лепесток лемнискаты Бернулли (см. раздел 1.1), который в полярных координатах описывается уравнением
r2 |
= a2 cos 2ϕ, ϕ [−π |
4 |
;π |
4 |
]. Вычислить криволинейный интеграл |
|
|
|
|
||
∫ |
x2 + y2 ds. |
|
|
|
|
L |
|
|
|
|
|
25

Решение. Так как r(ϕ) = a cos 2ϕ, |
r' (ϕ) = −a |
|
sin 2ϕ |
|
, то |
||||||||||
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
cos 2ϕ |
|||
r2 (ϕ) + (r' (ϕ))2 = a2 cos 2ϕ + a2 |
sin2 2ϕ |
= |
a2 |
|
|
. Учитывая, что в данном |
|||||||||
|
cos 2ϕ |
||||||||||||||
|
|
cos 2ϕ |
|
|
|
|
|
||||||||
случае x2 + y2 = r = a cos 2ϕ, на основании формулы (1.11) имеем |
|||||||||||||||
|
|
π |
|
|
|
|
|
|
adϕ |
|
|
|
|||
∫ |
x2 + y2 ds = ∫4 |
a |
cos 2ϕ |
|
= |
π a2 . |
|||||||||
|
|
|
|
|
|||||||||||
L |
|
−π |
4 |
|
|
|
|
|
cos 2ϕ |
|
2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.2 Криволинейный интеграл второго рода 1.2.1. Скалярные и векторные поля
Функцию u = u(x, y, z) , заданную на множестве G в пространстве
будем называть скалярным полем, заданным на этом множестве. Примером скалярного поля может служить поле температуры или электрического потенциала. Будем предполагать, что функция u = u(x, y, z) имеет
непрерывные частные производные по всем переменным. Если эти производные не обращаются одновременно в нуль, то уравнение u(x, y, z) = C (C = const) определяет некоторую поверхность без особых
точек, вдоль которой величина u = u(x, y, z) сохраняет постоянное значение, такая поверхность называется поверхностью уровня. Если
функция |
u = u(x, y) задана |
на |
плоскости, |
то |
уравнение |
||
u(x, y) = C |
определяет линии |
уровня |
скалярного поля. |
Например, если |
|||
скалярное поле задано функцией, u(x, y) = x2 + y2 |
, то линиями уровня |
||||||
скалярного поля является семейство окружностей x2 |
+ y2 |
= C. |
|
||||
Векторную |
функцию |
a(x, y, z) = (X (x, y, z),Y(x, y, z), Z(x, y, z)), |
|||||
определенную в каждой точке множества G будем называть векторным полем заданным на множестве G. Примером векторного поля может служить силовое поле или поле скоростей.
Векторные поля могут быть стационарными и нестационарными. В
первом случае вектор поля зависит не только от точки, но и от времени, во втором – только от точки. Можно также выделить однородные и неоднородные векторные поля. Значением однородного векторного поля во всех точках области является один и тот же вектор, неоднородное векторное поле в разных точках принимает разные значения. В
дальнейшем под векторным полем будем понимать стационарное
векторное поле.
Пусть скалярное поле u дифференцируемо в области G . Тогда ему можно поставить в соответствие векторное поле:
26
JJJJJG |
G |
G |
G |
gradu = ux' |
i |
+u'y j +uz' |
j.Как известно, уравнение касательной плоскости |
в точке M(xo, y0, z0) к поверхности уровня функции u = u(x, y, z) имеет вид:
u' |
|
|
(x − x ) +u' |
|
|
( y − y ) +u' |
|
|
(z − z |
0 |
) = 0. Следовательно, градиент |
||
x |
|
M |
0 |
y |
|
M |
0 |
z |
|
M |
|
|
|
|
|
|
|
|
|
|
|
||||||
скалярного поля ортогонален к поверхности уровня в данной точке, указывая, тем самым, направление максимального роста скалярного поля.
Скорость этого роста равна модулю (длине) вектора градиента. Функция
JJJJG u = u(x, y, z) называется потенциалом векторного поля gradu.
G
Векторное поле a(x, y, z) = (X (x, y, z),Y(x, y, z), Z(x, y, z)) называется
потенциальным полем, если существует функция u = u(x, y, z) , такая, что |
|||
G |
JJJJJG |
|
|
a(x, y, z) = gradu. |
|
||
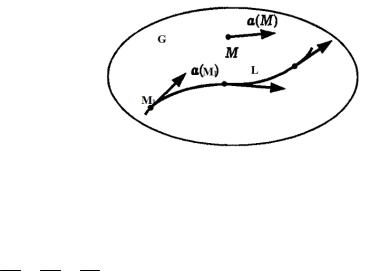
Линия |
L, |
вектор |
Gкасательной к которой в каждой точке M L , |
коллинеарен |
вектору |
a(M ) в этой точке называется векторной линией |
|
G |
|
|
|
поля a(M ) (Рис.1.3.1).
Рис.1.3.1
Так как вектор касательной пропорционален вектору (dx, dy, dz), то для
нахождения векторных линий получаем систему дифференциальных уравнений: dxX = dyY = dzZ .
Пример 1.10. Задано скалярное поле u(x, y) = x2 y.
1)Построить линии уровня скалярного поля.
2)Найти векторное поле, для которого функция u(x, y) = x2 y является
потенциалом.
3) Построить векторные линии этого поля.
Решение.
1). Линии уровня: x2y = C (семейство гипербол). |
|||
JJJJJG |
G |
+ x2 |
G |
2).Векторное поле: gradu = 2xy i |
j. |
||
27
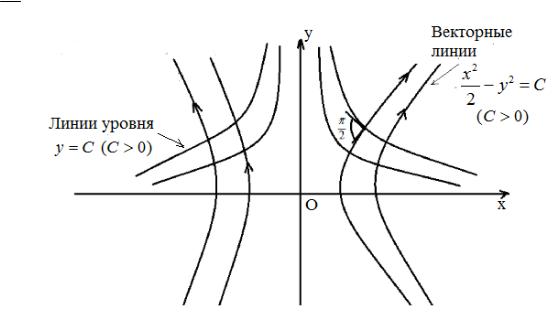
3) Векторные линии : |
dx |
= |
dy |
или |
xdx = 2 ydy → d |
x2 |
= dy |
2 |
. Откуда |
2xy |
x2 |
2 |
|
||||||
|
|
|
|
|
|
|
x2 − y2 = C (семейство гипербол) (рис. 1.3.2) 2
G Рис. 1.3.2
Замечание. Если поле a является градиентом потенциала u(x, y, z), то его
векторные линии ортогональны поверхностям уровня этого потенциала: u(x, y, z) = C.
1.2.2. Задача о работе силового поля. Понятие криволинейного |
|
|||||
|
интеграла второго рода |
JJJJJJG |
|
|
||
|
|
JJJJJG |
|
на оси |
||
Пусть задано силовое поле F(M ) . Проекции вектора силы F(M ) |
||||||
Ox и Oy обозначим, соответственно, через |
X (x, y), Y(x, y) . |
Пусть |
||||
материальная точка перемещается вдоль некоторой кривой |
AB |
в |
||||
плоскости xOy |
и в каждой точке |
M ее пути на точку действует сила |
||||
JJJJJJG |
|
|
|
|
|
|
F(M ) . Определим работу этого силового поля при перемещении |
||||||
материальной точки вдоль некоторой кривой AB от точки A к точке B.. |
||||||
Будем считать, что кривая AB является гладкой. |
A0 = A, A1 ,..., An = B , |
|||||
Разобьем |
кривую |
АВ |
точками |
|||
( Ai = Ai (xi , yi ), i = 0,1,..., n, ) |
на элементарные дуги |
Ai−1 Ai с длинами |
∆si |
и |
||
kk
выберем на каждой из таких дуг точку Mi (xi , yi ) (рис.1.3.3).
28
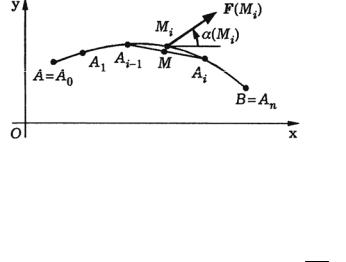
Рис.1.3.3
Если выбранное разбиение кривой AB достаточно мелкое, то можно принять два допущения:
1) перемещение материальной точки на участке Ai−1 Ai ее пути является прямолинейным, т.е. из положения Ai−1 в положение Ai точка перемещается вдоль прямолинейного отрезка длиной ∆si ;
2) сила, действующая на материальную точку при ее перемещении на
JG JG kk
участке Ai−1 Ai , постоянна и совпадает с F(Mi ) = F(xi , yi ).
При этих допущениях работа силы при перемещении материальной точки M из положения Ai−1 в положение Ai вдоль элементарной дуги
Ai−1 Ai , i =1,..., n, может быть записана с помощью скалярного произведения
(JJJJJJG JJJJJG
F(Mi Ai−1 Ai ). Суммируя работу силы по всем элементарным дугам Ai−1 Ai
мы получаем приближенную формулу для работы А, которую сила совершает при перемещении материальной точки по криволинейному пути
AB : |
JJJJJJG |
JJJJJG |
). |
|
n |
|
|||
Α ≈ ∑(F(Mi |
Ai−1 Ai |
(1.12) |
||
i=1
Погрешность этой формулы, определяемая принятыми допущениями, будет тем меньше, чем мельче разбиение кривой AB . Поэтому естественно в качестве точного значения работы принять предел суммы в правой части
(1.12) при λ = max ∆si → 0, т.е. считаем по определению, что
i
|
|
|
n |
JJJJJJG |
JJJJJG |
). |
|
|
|
|
Α = limλ→0 |
∑(F(Mi |
Ai−1 Ai |
|
(1.13) |
||
|
|
|
i=1 |
|
|
|
|
JJJJJG |
Обозначим через ∆xi = xi − xi−1 , |
∆yi = yi − yi−1 |
проекции вектора Ai−1 Ai |
||||||
на координатные оси. Тогда в соответствии с правилом вычисления |
||||||||
скалярного произведения |
|
|
|
|
|
|
||
|
n |
JJJJJJG JJJJJG |
|
n |
kk |
kk |
|
|
Α = limλ→0 |
∑(F(Mi Ai−1 Ai )= limλ→0 ∑(X (xi , yi )∆xi |
+Y(xi , yi )∆yi ). |
(1.14) |
|||||
|
i=1 |
|
|
i=1 |
|
|
|
|
Таким образом, вычисление работы привело нас к нахождению предела интегральных сумм нового вида. К составлению сумм вида (1.14) с последующим переходом к пределу приводит не только задача о работе,
29
поэтому совсем не обязательно всегда считать, что функции X (x, y) и Y(x, y) - проекции сил.
Рассмотрим на плоскости xOy гладкую кривую AB. Зададим на ней
направление движения от точки A к точке B . Кривую с установленным на ней направлением движения назовем ориентированной кривой. Пусть
на кривой |
AB |
заданы непрерывные |
функции |
X (x, y) и Y(x, y) , |
иначе |
||||||||
говоря, задана вектор-функция |
G |
|
|
G |
G |
Выберем |
|||||||
F(x, y) = |
X (x, y) i |
+Y(x, y) j . |
|||||||||||
разбиение |
T ={A0 , A1 ,..., An} |
кривой |
AB |
с |
точками |
деления |
|||||||
A0 = A, A1 ,..., An |
= B . Длины элементарных дуг Ai−1 Ai |
обозначим через ∆si , |
|||||||||||
а максимальную из этих длин – через λ = λ(T) . Возьмем на каждой дуге |
|||||||||||||
Ai−1 Ai |
|
|
|
|
|
kk |
|
|
|
|
|
|
|
|
по |
точке Mi (xi , yi ) , |
и |
вычислим |
значение |
функции |
|||||||
JG |
|
|
kkG |
kkG |
в |
этой |
точке. |
Обозначим |
через |
||||
F(M |
) = X (x , y ) i |
+Y(x , y ) j |
|||||||||||
i |
|
|
i |
i |
i |
i |
|
|
JJJJG |
|
|
|
|
∆xi = xi |
− xi−1 , ∆yi = yi − yi−1 |
проекции векторов Ai−1 Ai |
на координатные оси |
||||||||||
Ox иOy . Если движение по проекции происходит в сторону увеличения x |
||||
(или y ), то проекцию ∆xi |
|
JJJJG |
|
|
или ∆yi вектора Ai−1 Ai |
считаем положительной, |
|||
в противном случае – отрицательной. Составим сумму вида |
|
|||
n |
kk |
kk |
|
|
∑X (xi , yi )∆xi |
+Y(xi , yi )∆yi |
. |
(1.15) |
|
i=1
Эту суммуJGназывают интегральной суммой вдоль кривой AB для векторфункции F(x, y).
Если существует предел интегральных сумм (1.15) при λ = max ∆si → 0, |
||||||
|
|
|
|
|
i |
|
не зависящий ни от способа разбиения кривой AB на элементарные дуги, |
||||||
ни от выбора |
точек Mi на этих дугах, то этот предел называют |
|||||
криволинейным интегралом второго рода вдоль кривой AB от вектор- |
||||||
JG |
|
|
|
∫ X (x, y)dx +Y(x, y)dy. |
|
|
функции F(x, y) |
и обозначают символом |
Итак, по |
||||
определению |
|
|
|
AB |
|
|
|
|
|
kk |
kk |
|
|
∫ X (x, y)dx +Y(x, y)dy = λ=maxlim∆s |
n |
|
||||
→0 ∑X (xi , yi )∆xi |
+Y(xi , yi )∆yi . |
(1.16) |
||||
AB |
i |
i |
i=1 |
|
|
|
|
|
|
|
|||
Замечание 1. Кривая AB называется линией или контуром интегрирования, точка A – начальной, точка B – конечной точкой интегрирования.
Замечание 2. Если кривая L = AB замкнутая, то для обозначения интеграла используют символ v∫X (x, y)dx +Y(x, y)dy . Такой интеграл
L
иногда называют контурным интегралом. В случае замкнутого контура
30
