
Ми10 крив и пов
.pdfТеорема 2.2. (Теорема существования поверхностного интеграла второго рода)
Если функция Z(x, y, z) непрерывна вдоль кусочно-гладкой поверхности Q ,
то поверхностный интеграл второго рода существует.
(Доказательство теоремы смотрите, например,[1]). Аналогично можно показать, что
|
|
n |
n |
|
|
∫∫Y(x, y, z)dxdz =limd→0 ∑Y(xi , yi , zi )∆xi∆zi |
=limd→0 ∑Y(Mi )cosβi∆qi |
=∫∫Y(x, y, z)cosβdq; |
|||
Q |
|
i=1 |
i=1 |
Q |
|
|
|
n |
n |
|
|
∫∫X(x, y, z)dydz =limd→0 |
∑X(xi , yi , zi )∆yi∆zi |
=limd→0 ∑X(Mi )cosαi∆qi |
=∫∫X(x, y, z)cosαdq. |
||
Q |
|
i=1 |
i=1 |
Q |
|
Следовательно, имеем: |
|
|
|
||
JG |
G |
= ∫∫(X (x, y, z)cosα +Y(x, y, z)cos β +Z(x, y, z)cosγ)dq = |
|||
∫∫(F(M ) n(M ))dq |
|||||
Q |
|
Q |
|
|
|
|
= ∫∫X (x, y, z)dydz +Y(x, y, z)dxdz + Z(x, y, z)dxdy. |
(2.23) |
|||
|
Q |
|
|
|
|
Интеграл ∫∫X (x, y, z)dydz +Y(x, y, z)dxdz + Z(x, y, z)dxdy называют
Q
обычно составным поверхностным интегралом второго рода. Формула (2.23) устанавливает связь между поверхностными
интегралами первого и второго рода. |
|
|
||
Замечание 1. Если задано векторное поле |
G |
G |
||
JJJJJJG |
G |
|
||
F(M ) = X (x, y, z) i |
+Y(x, y, z) j |
+Z(x, y, z) k , |
||
где X = X (x, y, z); Y =Y(x, y, z); Z = Z(x, y, z) – |
непрерывные функции, то |
|||
поверхностный интеграл второго рода |
|
|
||
∫∫X (x, y, z)dydz +Y(x, y, z)dxdz + Z(x, y, z)dxdy определяет поток
Q
векторного поля через поверхность Q .
Замечание 2. В ситуации, когда поверхностный интеграл вычисляется по замкнутой поверхности Q , для него часто используют специальное
обозначение ∫∫wX (x, y, z)dydz +Y(x, y, z)dxdz + Z(x, y, z)dxdy.
Q
2.3.3. Свойства поверхностного интеграла второго рода
Сформулируем свойства поверхностного интеграла второго рода на примере одного его слагаемого, соответствующего функции Z(x, y, z) .
1)При изменении стороны поверхности интеграл меняет знак.
2)Свойства линейности:
∫∫(c1Z1(x, y,z) ±c2Z2(x, y,z))dxdy =c1∫∫Z1(x, y,z)dxdy±c2 ∫∫Z2 (x, y,z)dxdy, c1,c2 \.
Q Q Q
3) Свойство аддитивности: если поверхность Q разбита на конечное
81
число частей Qk Q, k =1,2,..., N, не имеющих общих внутренних
|
N |
точек, то ∫∫Z(x, y, z)dxdy = ∑∫∫Z(x, y, z)dxdy. |
|
Q |
k =1 Q |
|
k |
4) Интеграл ∫∫Z(x, y, z)dxdy по любой цилиндрической поверхности
Q
Q с образующими, параллельными оси Oz , равен нулю (рис. 2.18).
Первые три свойства, очевидно, следуют из определения поверхностного интеграла, как предела интегральных сумм (2.22*) G Докажем четвертое свойство. Так как единичный вектор нормалиGn(M ) к
поверхности Q параллелен плоскости xOy , т.е. угол между n(M ) и положительным направлением оси Oz прямой (рис.2.3.5), имеем cosγ = 0.
Следовательно, по формуле (2.23*) получаем
∫∫Z(x, y, z)dxdy = ∫∫Z(x, y, z)cosγdq = 0.
Q Q
2.3.4. Вычисление поверхностного интеграла второго рода
Если гладкая поверхность Q задана уравнением z = z(x, y) ,
(x, y) Sxy xOy , и выбрана ее верхняя сторона, т.е. единичный вектор
G
n(M ) нормали определен равенством (2.8), в котором радикалы взяты со
знаком плюс, то есть cosα = |
−zx' |
|
, cosβ = |
|
|
−z'y |
|
|
+ 1+(zx' )2 |
+(z'y ))2 |
+ |
1 +(zx' )2 |
+(z'y )2 |
||||
cosγ = |
|
|
1 |
|
|
. |
|
|
+ |
1 + (zx' (x, y))2 +(z'y (x, y))2 |
|
|
|||||
Поэтому, используя представление (2.16), для верхней стороны поверхности получим
∫∫Z(x, y, z)dxdy = ∫∫Z(x, y, z)cosγdq =
Q Q
|
= ∫∫Z(x, y, z(x, y))cosγ |
1 +(zx' (x, y))2 |
+(z'y (x, y))2 dxdy = |
|
|
||||||||||
|
Sxy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
' |
|
2 |
' |
|
2 |
|
|
= ∫∫Z(x, y, z(x, y)) |
|
|
|
|
|
|
|
1 +(zx |
(x, y)) |
|
+(zy |
(x, y)) |
|
dxdy = |
|
|
(x, y)) |
2 |
' |
(x, y)) |
2 |
|
|
|
|||||||
|
' |
|
|
|
|
|
|
|
|
|
|
||||
Sxy |
|
1 +(fx |
|
+(fy |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∫∫Z(x, y, z(x, y))dxdy. |
|
|
|
(2.24) |
||||||||
|
|
|
Sxy |
|
|
|
|
|
|
|
|
|
|
|
|
Для нижней стороны поверхности знак cosγ обратный, и поэтому в правой части (2.24) перед интегралом следует поставить знак минус:
82
∫∫Z(x, y, z)dxdy = −∫∫Z(x, y, z(x, y))dxdy. |
(2.25) |
|
Q |
Sxy |
|
Аналогично можно вычислить два остальных интеграла |
(2.23), если |
|
гладкая поверхность Q |
задана уравнением x = x( y, z) , ( y, z) Syz yOz , |
|
или y = y(x, z) , (x, z) Sxz xOz .
Пример 2.5. Вычислить поверхностный интеграл второго рода ∫∫ydxdz
Q
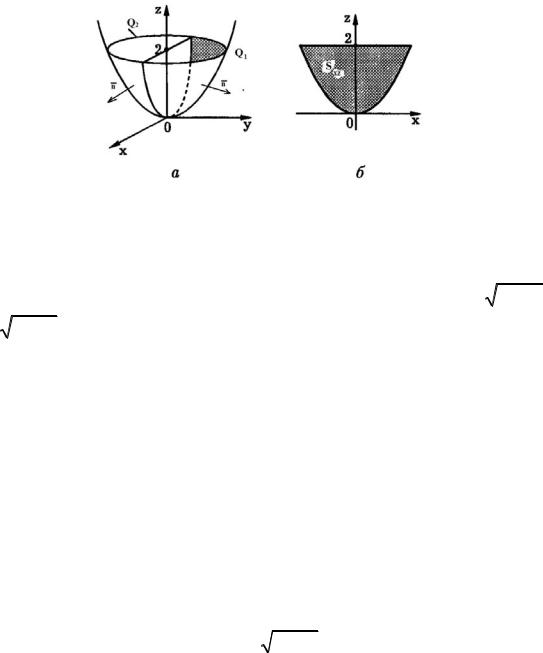
по внешней стороне части Q параболоида z = x2 + y2 , заключенной между плоскостями z = 0 и z = 2 (рис. 2.3.6, а).
Рис. 2.3.6
Решение. Разобьем поверхность Q координатной плоскостью xOz на две части Q1 и Q2 , расположенные по разные стороны от этой плоскости.
Поверхности Q |
и Q представляют собой графики функций y = z − x2 |
и |
1 |
2 |
|
y = − z − x2 . |
Эти функции имеют общую область определения Sxz |
– |
проекцию поверхности Q на плоскость xOz , которая описывается неравенствами 0 ≤ z ≤ 2, z ≥ x2 (рис. 2.3.6, б). В соответствии со
свойством аддитивности поверхностного интеграла второго рода запишем
∫∫ydxdz = ∫∫ydxdz + ∫∫ydxdz.
Q |
Q1 |
Q2 |
Выбор внешней стороны поверхности Q означает выбор правой стороны |
||
Q ( угол между единичным вектором нормали n(M ) и осью Oy острый) и |
|
1 |
G |
левой стороны Q2 ( угол между единичным вектором |
нормали n(M ) и |
осью Oy тупой ). Так как мы проектируем поверхность |
Q в плоскость |
xOz , то определяем угол между единичным вектором нормали и осью Oy . Для поверхности Q1 с выбранной стороной имеем
∫∫ydxdz = ∫∫ z − x2 dxdz ,
Q1 Sxz
83
где левая часть равенства – это поверхностный интеграл, а правая часть – двойной. Для поверхности Q2 с выбранной стороной (левой) имеем
|
|
∫∫ydxdz = −∫∫− |
z − x2 dxdz = ∫∫ |
|
|
|
z − x2 dxdz. |
|
|
|||||||||||||||||||||||||
|
|
Q2 |
|
|
|
|
|
Sxz |
|
|
|
|
|
|
|
|
|
|
Sxz |
|
|
|
|
|
|
|
|
|
|
|||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
∫∫ydxdz = ∫∫ydxdz + ∫∫ydxdz = 2∫∫ |
|
|
z − x2 dxdz. |
|
||||||||||||||||||||||||||||
|
|
Q |
|
|
|
|
Q1 |
|
|
|
|
Q2 |
|
|
|
|
Sxz |
|
|
|
|
|
|
|
|
|
||||||||
Вычислим двойной интеграл: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
∫∫ |
z − x2 dxdz = ∫2 |
dx∫2 |
z − x2 dz = |
|
2 |
|
∫2 |
(z − x2 )3/ 2 |
|
2x2 dx = = |
2 |
|
∫2 |
(2 − x2 )3/ 2 dx = |
||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||
3 |
|
|||||||||||||||||||||||||||||||||
Sxz |
|
− 2 |
x2 |
|
|
|
|
|
|
− 2 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
− 2 |
|
|||||||||
|
|
x = |
|
|
2 sin t |
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
||||||
|
= |
dx = |
|
2 cos tdt |
= |
2 |
∫2 |
4cos4 tdt = |
2 |
|
∫2 |
(1 + cos 2t)2 dt = |
||||||||||||||||||||||
|
3 |
|
||||||||||||||||||||||||||||||||
|
|
t1 = − |
π |
, t2 |
= |
π |
|
− |
π |
|
|
|
|
|
|
3 |
|
− |
π |
|
|
|
|
|
|
|
||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
2 |
|
|
π |
|
|
|
|
π |
|
|
|
|
1 |
|
π |
|
1 |
|
|
|
|
|
|
|
π |
|
|
|
|||
|
= |
|
t |
2π +sin 2t |
2π |
+ |
|
t |
2π |
+ |
sin 4t |
2π |
=π . |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
3 |
|
|
− |
2 |
|
|
|
− 2 |
|
|
2 |
|
− 2 |
8 |
|
|
|
|
|
|
|
− 2 |
|
|
|
||||||
Таким образом ∫∫ydxdz = 2π .
Q |
JJJJJG |
G |
G |
G |
|
||||
Пример 2.6. Вычислить поток векторного поля F(M ) = −x2 z i |
+ y j +2 |
k |
||
через поверхность Q – внешнюю сторону части эллипсоида 4x2 + y2 + 4z2 = 4 , расположенную в первом октанте (Рис.2.3.7).
Решение. Поток векторного поля определяется поверхностным интегралом второго рода (замечание 1.)
PQ = ∫∫−x2 zdydz + ydxdz + 2dxdy.
Q
Представим данный поверхностный интеграл в виде суммы трех интегралов:
84

Рис.2.3.7
PQ = ∫∫−x2 zdydz + ydxdz + 2dxdy = ∫∫−x2 zdydz + ∫∫ydxdz + ∫∫2dxdy.
Q Q Q Q
Преобразуем каждый из них в двойной интеграл:
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
y2 |
2 |
|
|
|
|
|
|
|
|
|
y2 |
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
y2 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
∫∫−x zdydz=+∫∫−x zdydz= |
x |
=1− |
|
|
|
|
|
−z |
|
=+∫∫− 1− |
|
|
−z |
|
zdydz=+∫∫ z |
|
+ |
|
|
|
|
|
−1 zdydz, |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
4 |
|
|
|
4 |
|
|
|
4 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Q |
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
yz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где знак плюс передGинтегралом означает, что угол между единичным |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
вектором нормали n к поверхности Q и осью Ox острый, Syz |
|
– |
|
проекция |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
поверхности Q на плоскость yOz , т.е. часть BOC эллипса |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
y2 + 4z2 |
≤ 4, y ≥ 0, z ≥ 0 (рис.2.3.7); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
∫∫ydxdz = +∫∫ydxdz = |
y = +2 |
|
1− x2 − z2 |
= + 2∫∫ |
|
1− x2 − z2 dxdz, где Sxz |
– |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Q |
|
|
|
|
|
|
|
|
Sxz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sxz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
проекция поверхности Q на плоскость xOz , т.е. часть AOC круга |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4x2 + 4z2 ≤ 4, x ≥ 0, z ≥ 0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
∫∫2dxdy = +2∫∫dxdy , где Sxy |
|
– часть AOB эллипса 4x2 + y2 |
≤ 4, x ≥ 0, y ≥ 0 . |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Q |
|
|
|
|
|
|
|
|
|
Sxy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Итак: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 1−z2 |
|
||||||||||
|
|
|
|
|
|
|
y |
2 |
|
|
|
|
1 |
|
|
|
|
4 |
− |
4z |
2 |
|
|
|
|
|
y |
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
3 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−(1− z2 ) y |
|
|
|
− |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
∫∫ z2 |
+ |
|
−1 zdydz = ∫zdz |
|
∫ |
|
|
z2 + |
|
−1 dy |
=∫zdz |
02 |
1 |
z |
|
+ |
|
|
|
|
|
= |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
S |
|
|
|
|
|
|
|
4 |
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
||||||||
|
yz |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y3 |
|
2 |
|
|
1−z2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
zdz |
|
|
|
|
2 |
|
|
2 1−z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3/ 2 |
|
|
|
|
2 |
|
|
3/ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
= |
|
−(1− z |
|
) y |
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
−2(1− z |
|
) |
|
|
|
+ |
|
|
|
(1 |
− z |
|
) |
|
|
|
zdz = |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
= − |
4 1 |
(1 − z |
2 |
) |
3/ 2 |
zdz = − |
4 |
|
|
− |
1 |
1 |
(1− z |
2 |
) |
3/ 2 |
d(1− z |
2 |
) = |
|
|
4 |
|
(1− z |
2 |
) |
5/ 2 |
|
1 |
|
= − |
|
|
4 |
; |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
3 ∫0 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
2 |
∫0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
15 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
85
|
|
|
|
|
|
|
x = ρ cosϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
z = ρsinϕ |
|
|
|
|
π / 2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||||
2∫∫ |
1 − x2 − z2 dxdz = |
|
dxdz = ρdρdϕ |
|
|
|
|
= 2 ∫ dϕ∫ 1− ρ2 ρdρ = |
|
|
|
|
||||||||||||||||||||||
Sxz |
|
|
|
|
0 ≤ϕ ≤ π , 0 |
|
≤ ρ ≤1 |
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π / 2 |
|
|
|
(1 − ρ2 )3/ 2 |
|
1 |
2 |
π / 2 |
|
π |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
= − ∫ |
dϕ |
|
|
|
|
|
|
= |
|
|
|
|
∫ dϕ = |
|
|
; |
|
|
|
|
|
|
|
|
|
|||||||
|
|
3 / 2 |
|
|
3 |
|
3 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
1 |
4−4 x2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
x = cost |
|
|
|
0 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
∫∫dxdy = ∫dx |
∫ |
dy = 2∫ 1 − x2 dx = |
dx = −sin tdt |
= −2 ∫ sin2 tdt = |
|
|
|
|
||||||||||||||||||||||||||
Sxy |
0 |
0 |
|
|
|
0 |
|
|
|
|
|
t |
[π / 2;0] |
|
|
π / 2 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
= π∫/ 2 |
(1 −cos 2t)dt = t |
|
π0 |
/ 2 − |
1 |
sin 2t |
|
π0 |
/ 2 |
= π . |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
G |
|
G |
|
|
|
|
|||||||||||
Следовательно, поток векторного поля |
|
|
JJJJJG |
|
|
+2 |
|
|
|
|
||||||||||||||||||||||||
|
|
F(M ) = −x2 z |
i |
+ y j |
k через |
|
|
|
||||||||||||||||||||||||||
поверхность Q равен: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
PQ =∫∫−x2zdydz+ydxdz+2dxdy =∫∫−x2zdydz+∫∫ydxdz+∫∫2dxdy =− |
4 |
|
+π |
+π = |
4π |
− |
|
4 |
. |
|||||||||||||||||||||||||
15 |
|
|
||||||||||||||||||||||||||||||||
Q |
|
|
|
|
|
Q |
|
|
Q |
|
|
|
|
Q |
|
|
|
|
3 |
3 |
|
15 |
||||||||||||
2.3.5. Формула Остроградского – Гаусса. Дивергенция векторного поля
Формула Остроградского-Гаусса связывает поверхностный интеграл по замкнутой поверхности с тройным интегралом по телу, ограниченному данной поверхностью.
Пространственная область G является односвязной, если для любой замкнутой поверхности, лежащей в G , ограничиваемая этой поверхностью область также целиком лежит в G (то есть пространственная область G не содержит полостей).
Рассмотрим замкнутую пространственную область Ω , которая снизу и сверху ограничена поверхностямиz = g2 (x, y) и z = g1 (x, y) , где
g2 (x, y) ≤ g1 (x, y), (x, y) Sxy и боковой цилиндрической поверхностью с образующими, параллельными оси Oz . Здесь Sxy – замкнутая область,
являющаяся проекцией пространственной области Ω на плоскость xOy
(рис. 2.3.8). Всякую замкнутую область описанного вида назовем
правильной областью в направлении оси Oz . Любая вертикальная прямая,
проходящая через внутреннюю точку такой области, пересекает ее границу только в двух точках.
Предположим, что замкнутая пространственная область Ω может быть разделена на конечное число областей, правильных в направлении оси Ox .
86

Пусть аналогичное свойство выполняется и в отношении двух других осей Oy и Oz . Такую область мы будем называть простой областью.
Рис.2.3.8
Теорема 2.3. (Формула Остроградского – Гаусса)
Если функции X (x, y, z), Y(x, y, z), Z(x, y, z) непрерывно дифференцируемы
в односвязной пространственной области G , то для любой простой замкнутой области Ω G , ограниченной кусочно-гладкой замкнутой поверхностью Q , верна формула Остроградского-Гаусса
∫∫wX (x, y, z)dydz +Y(x, y, z)dxdz + Z(x, y, z)dxdy =
Q+ |
|
|
|
|
|
|
|
|
|
= |
∫∫∫Ω |
|
∂X (x, y, z) |
+ |
∂Y(x, y, z) |
+ |
∂Z(x, y, z) |
|
(2.26) |
|
dxdydz, |
||||||||
|
|
∂x |
|
∂y |
|
∂z |
|
|
|
где Q+ – внешняя сторона поверхности Q .
Доказательство. Формула Остроградского-Гаусса распадается на три равенства, соответствующие трем подынтегральным функциям X (x, y, z) ,
Y(x, y, z) и Z(x, y, z) . Эти три равенства доказываются схожим образом, и
мы остановимся на одном из них, например на равенстве |
|
|||
∫∫wZ(x, y, z)dxdy = ∫∫∫ |
∂Z(x, y, z) |
dxdydz. |
(2.27) |
|
∂z |
||||
Q+ |
Ω |
|
|
|
Рассматриваемое равенство обладает свойством аддитивности. Это означает, что если замкнутая область Ω разбита на частичные области Ωk , k =1,2,..., m, ограниченные кусочно-гладкими поверхностями Qk , и для
этих замкнутых областей доказываемое равенство установлено, то это равенство будет выполняться и для самой области Ω.Так как замкнутая область Ω является простой, ее можно разбить на частичные области Ωk , k =1,2,..., m, являющиеся правильными в направлении оси Oz. Таким
образом, равенство (2.27) достаточно доказать для случая замкнутой области, правильной в направлении оси Oz .
87

Итак, |
пусть |
замкнутая |
область Ω G |
является правильной |
в |
||
направлении оси Oz . Это значит, что область |
Ω |
ограничена сверху и |
|||||
снизу |
поверхностями |
Q1 : z = g1 (x, y) ; |
Q2 : z = g2 (x, y) , |
где |
|||
g2 (x, y) ≤ g1 (x, y), (x, y) Sxy , |
Sxy |
– проекция пространственной области Ω |
|||||
на плоскость |
xOy ; сбоку |
– |
цилиндрической |
поверхностью Q3 |
с |
||
образующей, параллельной оси Oz , и направляющей – кусочно-гладкой границей замкнутой ограниченной области Sxy (рис.2.3.8). Тогда
Q = Q1 Q2 Q3 представляет собой замкнутую поверхность, внешнюю сторону которой обозначим через Q+ .
Из свойства аддитивности поверхностного интеграла второго рода имеем:
∫∫wZ(x, y, z)dxdy =∫∫wZ(x, y, z)dxdy + ∫∫wZ(x, y, z)dxdy + ∫∫wZ(x, y, z)dxdy.
Q+ |
Q1+ |
Q2+ |
Q3+ |
Интеграл ∫∫wZ(x, y, z)dxdy =∫∫Z(x, y, z)cosγdq = 0 |
(формула (2.23)), так как |
||
|
Q3+ |
Q3+ |
|
угол γ между единичным вектором нормали n к поверхности Q3 и осью
Oz равен |
π (рис. 2.3.8); |
|
|
|
|
2 |
|
|
|
∫∫wZ(x, y, z)dxdy = + ∫∫Z(x, y, g1 (x, y))dxdy |
( формула |
(2.24)), |
знак плюс |
|
Q1+ |
Sxy |
|
|
|
перед двойным интегралом означает, что угол γ |
между |
единичным |
||
вектором G |
|
|
|
|
нормали |
n к поверхности Q1+ и осью Oz острый; |
|
|
|
∫∫wZ(x, y, z)dxdy = − ∫∫Z(x, y, g2 (x, y))dxdy , |
знак минус перед двойным |
|||
Q2+ |
Sxy |
|
|
|
интегралом означает, что угол γ между единичным вектором нормали n к поверхности Q2+ и осью Oz тупой (рис. 2.3.8). Следовательно,
∫∫wZ(x, y, z)dxdy =∫∫Z(x, y, g1 (x, y))dxdy − ∫∫Z(x, y, g2 (x, y))dxdy =
Q+ |
Sxy |
Sxy |
|
|
= ∫∫(Z(x, y, g1 (x, y)) − Z(x, y, g2 (x, y)))dxdy. |
(2.28) |
|
|
Sxy |
|
|
С другой стороны,
∫∫∫∂Z(x, y, z) dxdydz = ∫∫ |
||
Ω |
∂z |
Sxy |
|
||
z=g1 ( x, y) |
∂Z(x, y, z) |
|
|
z=g1 ( x, y) |
|
dxdy ∫ |
dz =∫∫dxdy Z(x, y, z) |
|
= |
||
∂z |
|
z=g2 ( x, y) |
|||
|
|
||||
z=g2 ( x, y) |
Sxy |
|
|
|
|
|
|
|
|
= ∫∫(Z(x, y, g1 (x, y)) − Z(x, y, g2 (x, y))dxdy. |
(2.29) |
Sxy |
|
Сравнивая выражения для поверхностного интеграла (2.28) и для тройного интеграла (2.29) получаем требуемую формулу (2.27).
88
Замечание 1. Формулу Остроградского-Гаусса можно распространить на произвольную ограниченную пространственную область Ω, граница Q
которой состоит из конечного числа замкнутых кусочно-гладких поверхностей (область Ω в этом случае имеет полости). При этом в левой части формулы Остроградского-Гаусса поверхностный интеграл следует брать вдоль границы области Ω, т.е. необходимо суммировать поверхностные интегралы по всем поверхностям, составляющим границу, причем для внешней поверхности выбирается внешняя сторона, а для внутренних — внутренняя. Чтобы доказать такое обобщение формулы Остроградского-Гаусса, достаточно соединить произвольными гладкими поверхностями внешнюю часть границы области Ω с внутренними.
Замечание 2. На основании формулы (2.23), формулу Остроградского – Гаусса можно записать и так:
|
∂X (x, y, z) |
+ |
∂Y(x, y, z) |
+ |
∂Z(x, y, z) |
|
|
dxdydz = |
|||||
∫∫∫Ω |
∂x |
|
∂y |
|
∂z |
|
= ∫∫w(X (x, y, z)cosα +Y(x, y, z)cos β + Z(x, y, z)cosγ)dq
Q+
Замечание 3. Пусть в пространственной области G, Ω G, задано
JJJJJJG G G G
векторное поле F(M ) = X (x, y, z) i +Y(x, y, z) j +Z(x, y, z) k , где X = X (x, y, z); Y =Y(x, y, z); Z = Z(x, y, z) – непрерывно
дифференцируемые в области G функции, тогда формула Остроградского-Гаусса запишется следующим образом (см.
формулу(2.23)): |
|
|
|
|
|
|
|
|
|
|
JG |
G |
|
∂X (x, y, z) |
|
∂Y(x, y, z) |
|
∂Z(x, y, z) |
|
|
|
∫∫(F(M ) n(M ))dq |
= ∫∫∫ |
+ |
+ |
dxdydz. |
(2.30) |
|||||
Q+ |
|
Ω |
∂x |
|
∂y |
|
∂z |
|
|
|
Выражение ∂X (x, y, z) + |
∂Y(x, y, z) |
+ |
∂Z(x, y, z) |
называют дивергенцией |
||||||
|
∂x |
|
∂y |
|
∂z |
|
|
|
|
|
|
|
JJJJJG |
JG |
= |
∂X (x, y, z) |
+ |
∂Y(x, y, z) |
+ |
∂Z(x, y, z) . |
|
векторного поля F(M ) : divF(M ) |
||||||||||
|
|
|
|
|
∂x |
|
∂y |
|
∂z |
|
Формулу Остроградского-Гаусса, в терминах векторного поля, можно
сформулировать следующим образом.
JJJJJJG
Поток векторного поля F(M ) через внешнюю замкнутую поверхность Q+
JG
равен тройному интегралу от дивергенции векторного поля divF(M ) по
пространственной области Ω, ограниченной этой поверхностью: |
|
||
JG |
G |
JG |
|
∫∫(F(M ) n(M ))dq = ∫∫∫divF(M )dxdydz. |
(2.31) |
||
Q+ |
|
Ω |
|
Пример 2.7. С помощью формулы Остроградского – Гаусса вычислить |
||||
JJJJJJG |
G |
+ y2 |
G |
G |
поток векторного поля F(M ) = x2 |
i |
j + z2 |
k через внешнюю сторону |
|
89
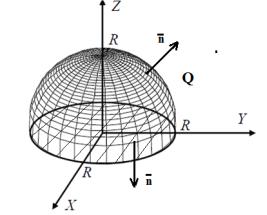
замкнутой |
|
поверхности Q , |
составленной из верхней части сферы |
|
x2 + y2 + z |
2 |
= R2 , z ≥ 0 |
и круга x2 + y2 ≤ R2 , z = 0 (рис.2.3.9). |
|
Решение. Здесь область Ω – верхняя половина шара |
||||
x2 + y2 + z |
2 ≤ R2 , z ≥ 0 |
. Дивергенция векторного поля |
||
JG |
|
∂X (x, y, z) + ∂Y(x, y, z) |
+ ∂Z(x, y, z) = 2x + 2 y + 2z. |
|
divF(M ) = |
||||
|
|
∂x |
∂y |
∂z |
Рис.2.3.9
Используя формулу Остроградского-Гаусса (2.31) , получим, что поток PQ
JJJJJG
векторного поля F(M ) через внешнюю поверхность Q+ определяется
равенством: |
|
G |
|
|
|
|
|
|
|
|
|
|
|
JG |
|
|
|
|
|
|
|
|
|
|
|
||
PQ = ∫∫(F(M ), n(M ))dq = ∫∫X (x, y, z)dydz +Y(x, y, z)dxdz + Z(x, y, z)dxdy = |
|||||||||||||
Q+ |
|
|
|
|
Q+ |
G |
|
|
|
|
|
|
|
= ∫∫x2dydz + y2dxdz + z2dxdy = ∫∫∫divF(M)dxdydz = 2∫∫∫(x + y + z)dxdydz = |
|||||||||||||
Q+ |
|
|
|
|
|
Ω |
|
Ω |
|
|
|
|
|
|
|
|
|
|
|
x = ρ cosϕsinθ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = ρsinϕsinθ |
|
|
|
|
|
|
|
|
|
|
= |
|
z = ρ cosθ |
|
= |
|
|
|
|
|
|
|
|
|
|
|
dxdydz = ρ2 sinθdρdϕdθ |
|
|
|
|
|
|
||
|
|
|
|
|
ϕ [0;2π],θ [0;π / 2], ρ [0; R] |
|
|
|
|
|
|
||
= 22∫π dϕπ∫/ 2 dθ∫R (cosϕsinθ +sinϕsinθ + cosθ)ρ3 sinθdρ = |
|||||||||||||
|
0 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
= 22∫π dϕπ∫/ 2 |
(cosϕsinθ +sinϕsinθ + cosθ)sinθdθ |
ρ4 |
|
|
R |
= |
|||||||
|
|
||||||||||||
|
|
|
|
||||||||||
|
|
0 |
0 |
|
|
|
4 |
|
|
0 |
|
||
= |
R |
|
(cosϕ |
+sinϕ) ∫ sin2 θdθ + |
|
|
|
|
|
||||
|
∫dϕ |
∫ cosθ sinθdθ = |
|||||||||||
|
|
4 |
2π |
|
|
π / 2 |
π / 2 |
|
|
|
|
||
|
2 |
0 |
|
|
0 |
0 |
|
|
|
|
|
|
|
90
