Ми10 крив и пов

51

2. Поверхностные интегралы

Поверхности

Поверхность в пространстве может быть задана как график некоторой

непрерывной функции:

D лежит в плоскости xOz . В этих трех случаях поверхность называют

явно заданной поверхностью.

где F(x, y, z) – непрерывная функция, которое не разрешено относительно

какой-либо из переменных. Тогда ее называют неявно заданной поверхностью.

Например, уравнение x2 + y2 + z2 − R2 = 0 задает в пространстве \3

поверхность, представляющую собой сферу радиуса R с центром в начале координат.

Если в уравнении явно заданной и неявно заданной поверхности

отсутствует, хотя бы одна переменная, то такую поверхность будем

называть цилиндрической поверхностью.

Наконец, поверхность Q может быть задана параметрическими уравнениями

x = x(u,v);

y = y(u,v); (u,v) D \2 ,

z = z(u,v),

где x(u,v) , y(u,v) , z(u,v) – непрерывные функции в их области

определения D. В этом случае говорят о параметрически заданной поверхности.

Например, сфера радиуса R с центром в начале координат может быть

Множество точек поверхности, соответствующих граничным точкам области D, образует границу (или край) этой поверхности. Точки поверхности, не принадлежащие ее границе, называют внутренними точками поверхности. Поверхность может не иметь границы. Такую

52

поверхность называют замкнутой. Примером замкнутой поверхности является сфера. Поверхность Q будем называть гладкой поверхностью,

если для любой ее внутренней точки существует такая окрестность в пространстве, что часть поверхности Q , попадающая в эту окрестность,

может быть представлена как явно заданная поверхность одним из уравнений (2.1) – (2.3) , причем функция f является непрерывно

дифференцируемой. В каждой внутренней точке гладкой поверхности существуют касательная плоскость и нормаль к этой поверхности.

Пусть поверхность Q задана неявно уравнением (2.4), в котором

то поверхность Q является гладкой и не имеет особых точек. Уравнение касательной плоскости в точке M (x0 , y0 , z0 ) Q имеет вид:

нормальный вектор касательной плоскости к поверхности Q в точке

которая в каждой точке поверхности Q задает единичный вектор нормали к этой поверхности. Двойной знак перед радикалом отвечает двум противоположным направлениям единичного вектора нормали.

Если cosα,cos β,cosγ – направляющие косинусы нормали к поверхности, то

непрерывно дифференцируема в области D . Тогда уравнение касательной плоскости в точке M (x0 , y0 , z0 ) Q запишется в виде:

53

касательной плоскости к поверхности Q в точке (x, y, z) Q .

Единичный вектор нормали и направляющие косинусы этого вектора запишутся следующим образом:

Гладкая поверхность называется ориентируемой или двусторонней,

если на ней можно выбрать непрерывный единичный вектор нормали (который ее и ориентирует), и неориентируемой или односторонней в

противном случае. (Примеры, лист Мебиуса)

Пример 2.1. Пусть поверхность Q – сфера F(x, y, z) = x2 + y2 + z2 − R2 = 0 .

нуль в единственной точке O(0,0,0) , не лежащей на сфере. Следовательно, сфера — двусторонняя поверхность, а непрерывная функция единичной

“ −”: nG(x, y, z) = −xR Gi + −yR Gj + −zR kG, то – внутреннюю сторону сферы . Приведенный пример показывает, что на практике большинство

рассматриваемых поверхностей являются двусторонними. Существуют ли односторонние поверхности?

54

Возьмем на поверхности Q замкнутый контур L, выбрав в качестве начальной некоторую точку M0 . Если поверхность двусторонняя, то на

выбранном контуре пределена непрерывная векторная функция, значением которой является единичный вектор нормали к поверхности. Но единичный вектор нормали в каждой точке поверхности может принимать лишь два возможных значения. Поэтому, задав единичный вектор нормали в точке M0 , мы тем самым однозначно определяем векторную функцию в

некоторой окрестности точки M0 . Обойдя весь контур, мы вернемся в точку M0 с однозначно определенным единичным вектором нормали. При

этом возможны две ситуации: либо конечное положение вектора нормали совпадет с начальным, либо нет. В последнем случае можно сделать вывод, что на поверхности нельзя задать непрерывное изменение единичного вектора нормали и что эта поверхность является односторонней.

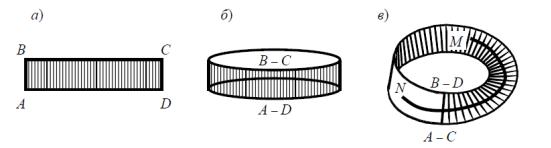
Простейшим примером односторонней поверхности является лист Мебиуса. Эту поверхность можно представить следующим образом. Возьмем прямоугольную полоску ABCD бумаги и склеим ее противоположные стороны АВ и CD, перекрутив эту полоску один раз (рис. 2.0). Выбор той или иной стороны полоски определяется выбором единичного вектора нормали. Если контур на поверхности пересекает линию склейки, то происходит переход с одной стороны полоски на другую. В результате при обходе по такому контуру единичный вектор нормали меняет направление.

Рис.2.0 a) полоса бумаги; б) склеенное из нее кольцо; в) лист Мёбиуса. Если поверхность Q двусторонняя, то на ней существует всего лишь

два способа выбора непрерывного единичного вектора нормали. Задав в каждой точке единичный вектор нормали так, чтобы он менялся непрерывно, мы тем самым определяем сторону поверхности. Поэтому в дальнейшем под стороной поверхности мы будем понимать заданную на этой поверхности непрерывную функцию вектора единичной нормали.

55

Наиболее часто встречающиеся в задачах поверхности

Одним из основных методов исследования геометрических свойств и формы поверхности по ее каноническому уравнению является метод сечений. Этот метод заключается в следующем: рассматривается сечение даннной поверхности координатными плоскостями и плоскостями, параллельными координатным плоскостям. По типу полученных линий пересечения делается вывод о форме поверхности.

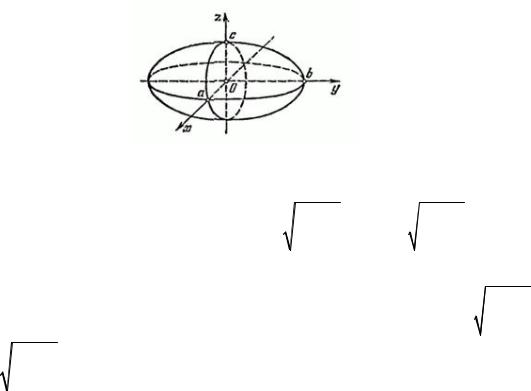
Поверхности второго порядка 1. Эллипсоид

симметричен относительно всех трех координатных плоскостей (х2 – симметрия относительно плоскости yOz и т.д.).

Если пересечь эллипсоид плоскостью z = h (|h|< c), параллельной плоскости х0у, получим:

Рис. 2.1

56

параллельной плоскости х0у, вырождается в точку ( x = 0, y = 0, z = ± c) . При | h |> c , эллипсоид с плоскостью z = h не пересекается.

Аналогично можно показать, что пересечение эллипсоида с плоскостями у

= h (|h| < b) и х = h (|h| < а) – тоже эллипсы.

Учитывая все вышесказанное, приходим к выводу, что эллипсоид – это поверхность, изображенная на рис. 2.1.

Замечание. Если все три полуоси эллипсоида равны (a = b = c = R) , то получится сфера с центром в начале координат радиуса

R : x2 + y2 + z2 = R2 .

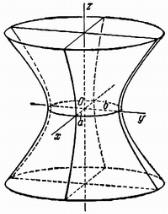
2. Однополостный гиперболоид

Рис. 2.2

Так как в уравнении поверхности все переменные в четных степенях, то поверхность симметрична относительно всех трех координатных плоскостей. При сечении однополостного гиперболоида плоскостью у = 0,

при сечении плоскостью х = 0, получится гипербола, лежащая в плоскости

уравнения которого, как уравнения кривой в пространстве, имеют вид:

57

Полуоси этого эллипса возрастают с возрастанием |h|:

При h = 0 они наименьшие, равные а и b, таким образом, однополостный гиперболоид – это поверхность, изображенная на рисунке 2.2.

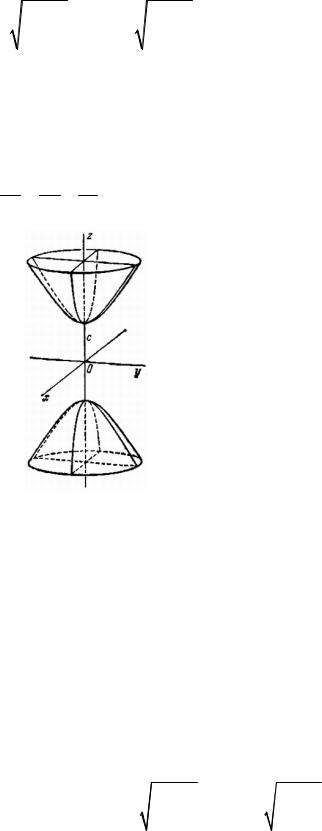
3. Двуполостный гиперболоид

Каноническое уравнение: x2 + y2 − z2 = −1. a2 b2 c2

Рис. 2.3

Аналогично ранее рассмотренным случаям, координатные плоскости являются плоскостями симметрии этой поверхности. Пересекая двуполостный гиперболоид координатными плоскостями xOz ( y = 0) и

yOz (x = 0) , получим соответствующие гиперболы:

Если двуполостный гиперболоид пересекать плоскостями z = h, |h| > c, то

точку (х = 0, у = 0, z = ±с). При |h| < c плоскость z = h не пересекает данную

58

определяет пустое множество. Следовательно, используя метод сечений, приходим к выводу, что двуполостный гиперболоид – это поверхность, изображенная на рис. 2.3.

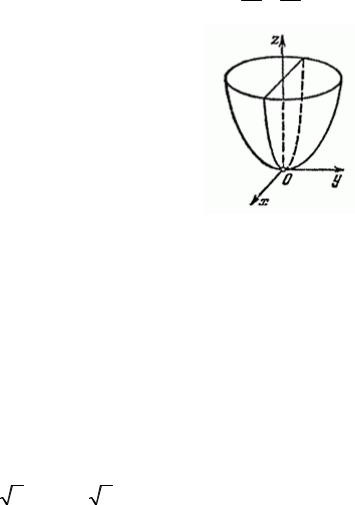
4. Эллиптический параболоид

Каноническое уравнение: z = x2 + y2 . a2 b2

Рис. 2.4

Для этой поверхности плоскостями симметрии являются плоскости х0z (у = 0) и у0z (х = 0). Эллиптический параболоид расположен в полупространстве z ≥ 0. При пересечении эллиптического параболоида координатными плоскостями х0z (у = 0) и у0z (х = 0), получаются,

Плоскость z = 0 и исследуемая поверхность имеют одну общую точку − начало координат, так как система уравнений:

имеет единственное решение (х = 0, у = 0, z = 0).

Обобщая полученные результаты, приходим к выводу, что эллиптический параболоид – поверхность, изображенная на рис. 2.4.

59

5. Гиперболический параболоид

Каноническое уравнение: z = x2 − y2 . a2 b2

Кординатные плоскости х0z (у = 0) и у0z (х = 0) – плоскости симметрии этой поверхности. Пересекая поверхность плоскостью х0z, (у = 0), получаем параболу:

При пересечении гиперболического параболоида плоскостью х = h, получится парабола

При различных значениях h получается семейство парабол, лежащих в плоскостях, параллельных плоскости y0z. Причем вершины всех парабол лежат на параболе (2.8* ) . В частности, при х = 0 получается парабола:

Рис. 2.5

60