Задача 3.

Камень брошен со скоростью v₀ под углом  к горизонту. Пренебрегая сопротивлением воздуха, найти: зависимость вектора скорости v от времени движения t, вектор r перемещения камня за время t, среднюю скорость v_cp камня за первые t секунд полета, максимальную высоту подъема Н, дальность полета S и полное время полета Т, векторы тангенциального a_ и нормального a_n ускорения камня как функцию времени t, радиус кривизны траектории R как функцию t и уравнение траектории y = f (х).

Решение.

В задачах подобного рода отсутствие сопротивления воздуха означает постоянство ускорения камня: a = g, где g – вектор ускорения свободного падения. Этот факт обусловлен тем обстоятельством, что в отсутствие сопротивления воздуха на камень действует единственная сила – сила тяжести mg (m – масса камня). В силу второго закона Ньютона:

ma = mg,

откуда a = g.

Для нахождения v(t) вспомним, что a = dv/dt. Поскольку a = g, то v – линейная функция времени:

v(t) = gt + v₀ (1),

где v₀ – некоторый постоянный вектор. Выясним смысл v₀. Полагая t = 0, получим:

v (0) = v₀,

то есть v₀ – вектор начальной скорости камня.

Найдем радиус-вектор r(t). Вспоминаем, что v = dr/dt. В нашем случае v определяется формулой (1). Поэтому:

dr/dt = gt + v₀ (2).

Интегрируя (2) по времени получим:

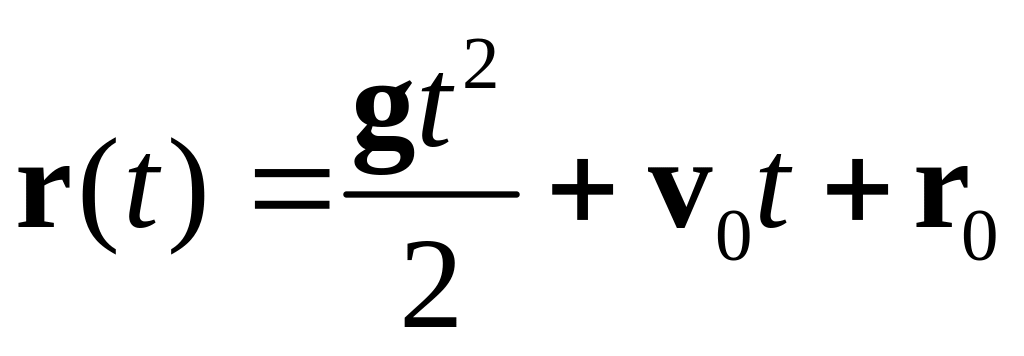(3).

При t = 0 r(0) = r₀. Если выбрать начало координат в точке бросания, то r(0) = 0. Таким образом, r₀ = 0 и:

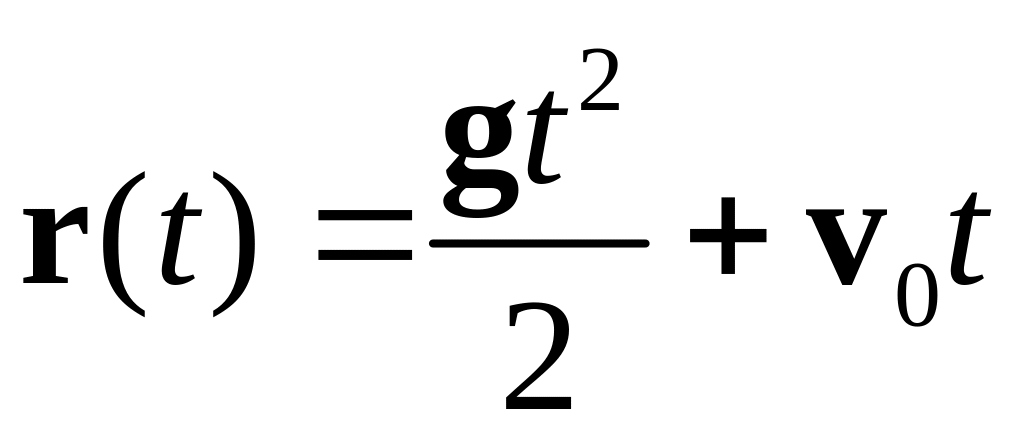(4).

Полученный результат показывает, что траектория камня – плоская кривая, лежащая всеми своими точками в вертикальной плоскости, образованной векторами g и v₀.

Средняя скорость v_cp(t) камня за первые t секунд полета по определению равна:

,

согласно (3) получаем:

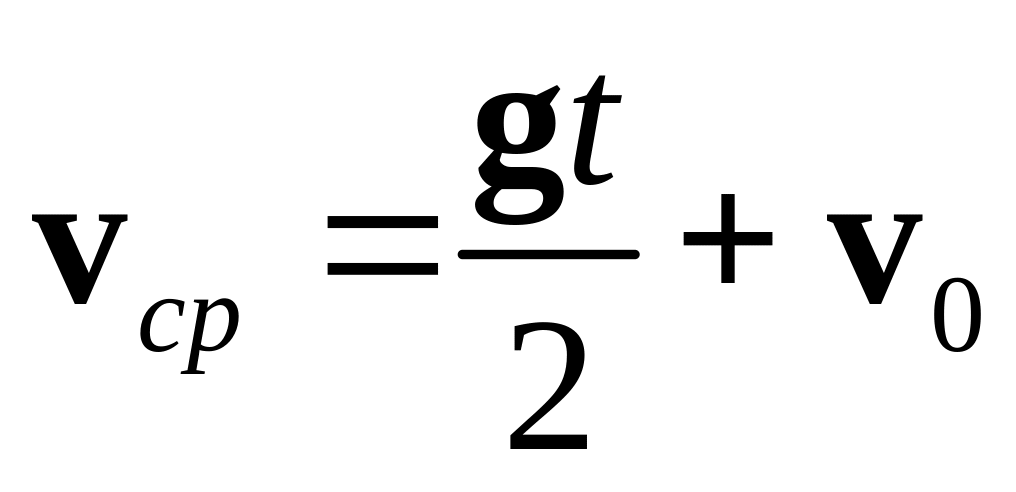(5).

Как видим v_ср(t) ≠ v (t). Результаты (1) – (5) иллюстрируются рис. 1.

Для нахождения максимальной высоты подъема Н заметим, что в наивысшей точке траектории вертикальная компонента скорости v_y равна нулю. Действительно, если бы это было не так, то тело поднималось бы, либо опускалось, но в любом случае оно не могло бы находиться в наивысшей точке траектории.

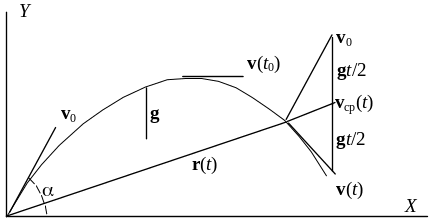
Рис. 1

Выберем систему координат с осью OY, направленной вертикально вверх и горизонтальной осью OX, ориентированной так, чтобы плоскость XOY содержала вектор начальной скорости v₀. В этом случае, согласно (2), компоненты скорости равны соответственно:

_x(t) = ₀cos , v_y(t) = ₀sin – gt (6).

Из условия _y(t₀) = 0, найдем из (6) t₀ – время подъема на максимальную высоту:

t₀ = ₀sin  /g.

Координаты камня в момент t равны соответственно:

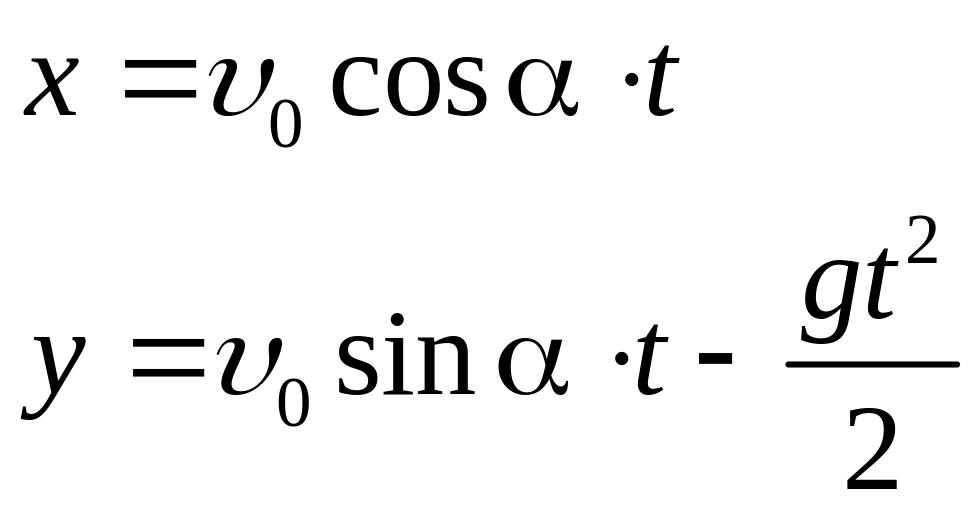(7).

Подставляя сюда найденное значение t₀, получим:

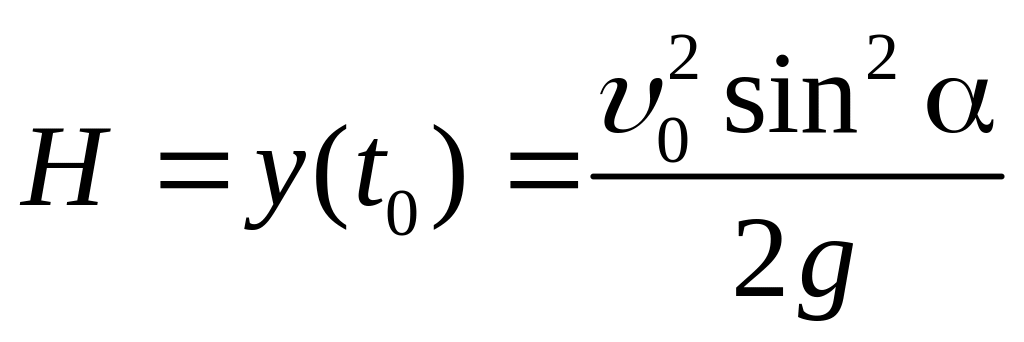
Для нахождения дальности полета S (расстояния между точкой падения и точкой бросания), заметим, что в точке падения y(t) = 0, откуда найдем время полёта Т:

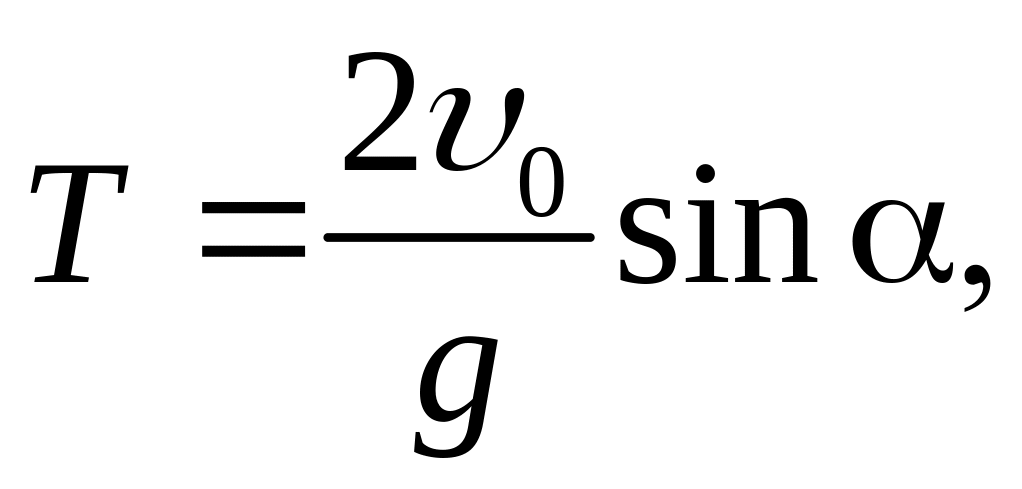
а также дальность полёта S:

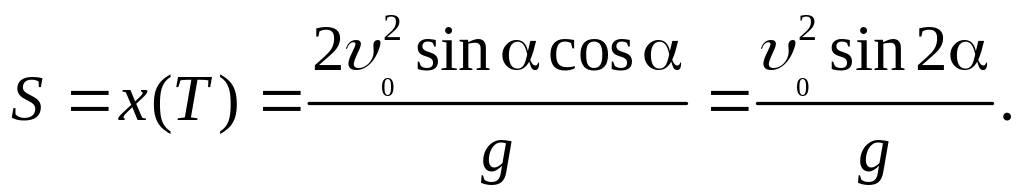
Рис. 2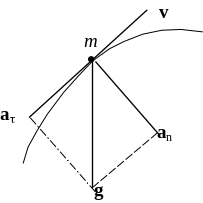

Заметим, что Т = 2t₀, т.е. время подъема t₀ на максимальную высоту равно половине времени полета камня Т и, тем самым, времени спуска. Отметим, что это справедливо только при игнорировании силы сопротивления воздуха. Подумайте: как будут соотноситься время подъема и время спуска, если учесть силу сопротивления воздуха?

Заметим также, что высота и дальность полёта пропорциональны квадрату начальной скорости тела.

Найдём теперь компоненты ускорения a_ и a_n. Заметим, что сумма этих векторов равна ускорению свободного падения (Рис. 2):

g = a_ + a_n.

Для нахождения величины тангенциального ускорения a_ найдем квадрат модуля скорости:

² (t) = (v(t), v(t)) = (v₀+gt, v₀+gt) =v₀² + 2(v₀, g)t +g² t² = ₀² – 2₀gt sin +g² t² (8)

Здесь мы воспользовались определением квадрата модуля вектора, как скалярного произведения вектора самого на себя:

|v|² = (v, v).

Дифференцируя обе стороны (8) по времени получим:

отсюда найдём тангенциальное ускорение:

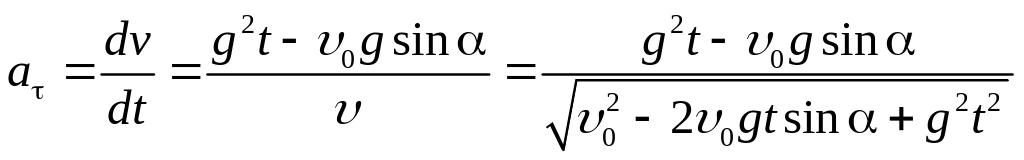(9)

Отметим, что a_, которое мы получили, это не модуль вектора |a_|, а проекция вектора a_ на направление вектора скорости v. Так, если a_ > 0, то a_ и v направлены в одну сторону, если a_ < 0, тo – в противоположные.

Найдем теперь a_n. Для этого учтем, что a_+ a_n = g (см. рис. 2). Так как a_ и а_n взаимно перпендикулярны, то:

g² = a_² + a_n²,

откуда получим:

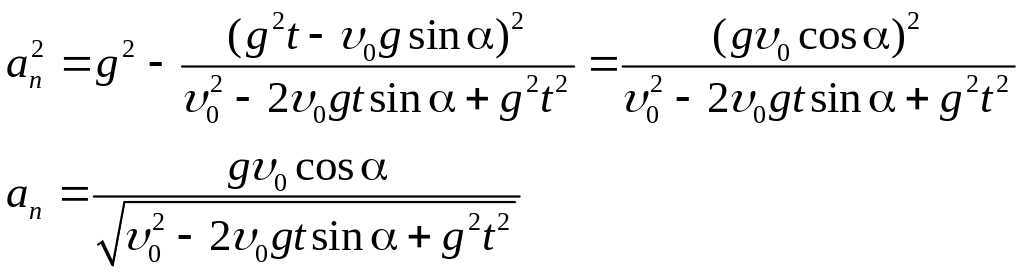(10).

Для нахождения радиуса кривизны траектории воспользуемся связью между a_n,  и R:

a_n = ²/R.

Отсюда с учетом (8) и (10):

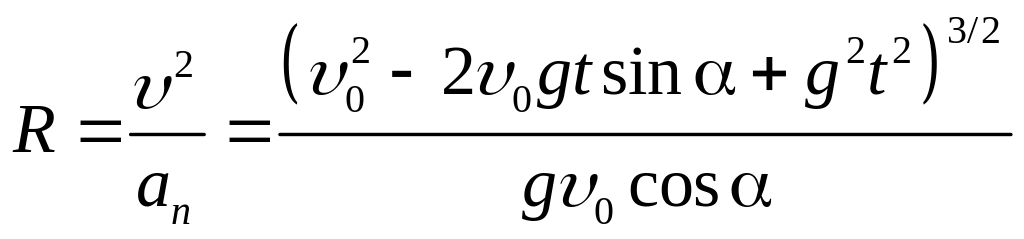(11).

Проанализируем полученные результаты. Выражение (9) для a_ показывает, что a_ < 0 при t < v₀ sin/g. Т.е. на восходящей части траектории d /dt < 0 и это означает, что скорость камня уменьшается. При t > ₀ sin/g ускорение a_ > 0 , и скорость камня растет на нисходящей части траектории.

Из (11) нетрудно видеть, что радиус кривизны R сначала уменьшается (т.к. числитель в (11) равен ^3/2, а скорость вначале уменьшается), а затем при t > ₀sin/g растет.

В частности, в точке бросания при t =0:

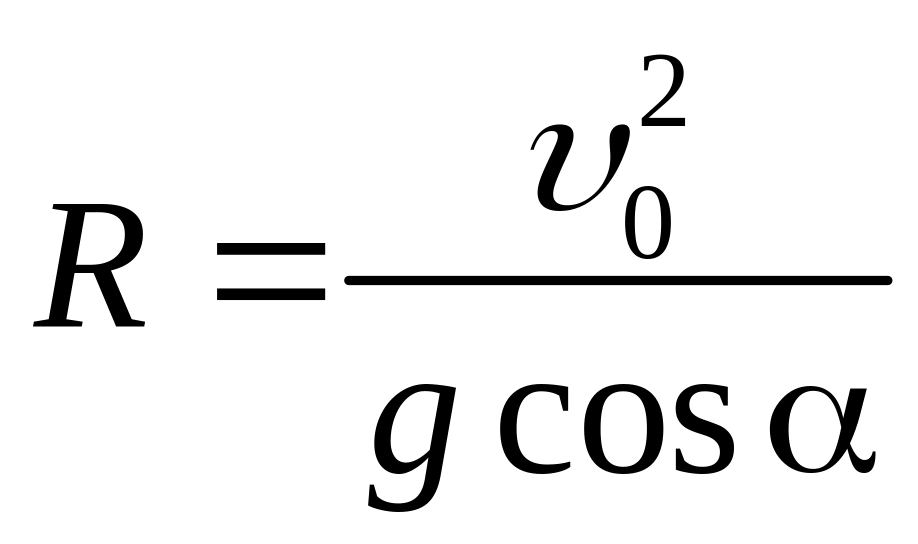
а в наивысшей точке траектории при t = ₀ sin/g :

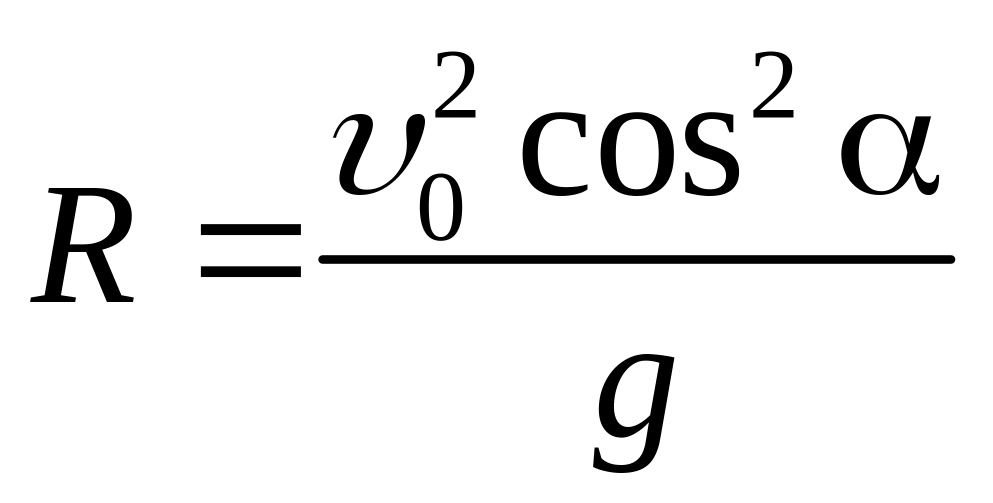
Уравнение траектории в параметрическом виде (x=x(t), y=y(t)) дается (7). Выразив t через x(t) и, подставив его во второе из уравнений (7), получим уравнение траектории в явном виде:

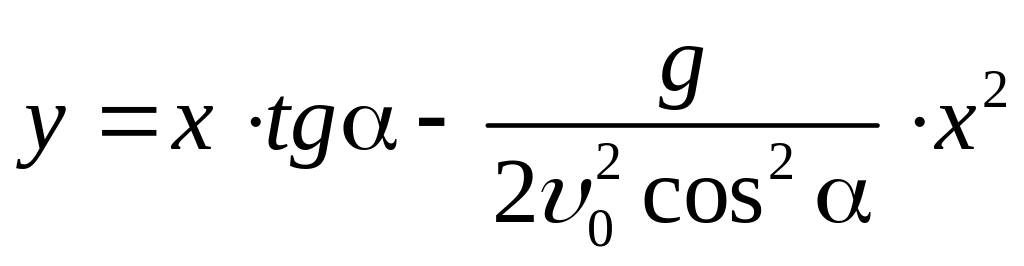(12)

Из (12) можно найти максимальную высоту подъема H и дальность полета S, найденные нами ранее из других соображений. Для нахождения S заметим, что у = 0 при x=S. Откуда с помощью (12) получим уравнение для S:

Сокращая на S, получим знакомый результат:

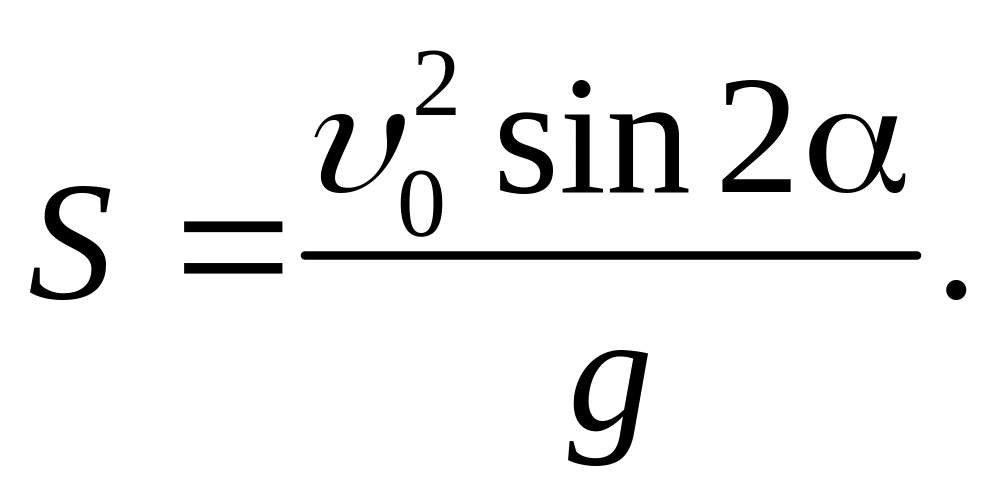
Для нахождения Н = max у(х) продифференцируем (12) по х:

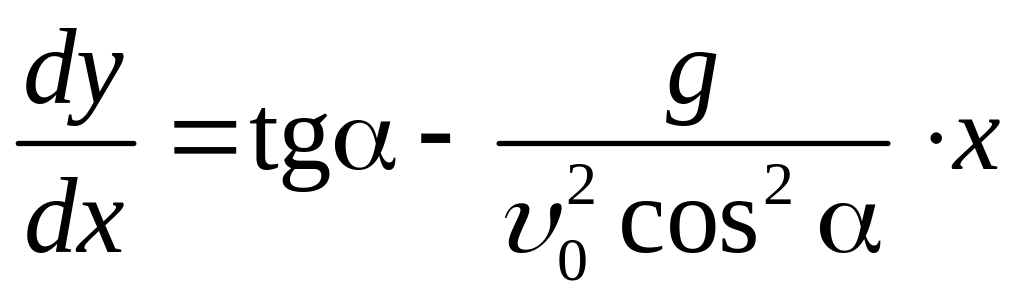
В точке максимума dy/dx = 0, откуда найдем х₀, соответствующее максимуму у(х):

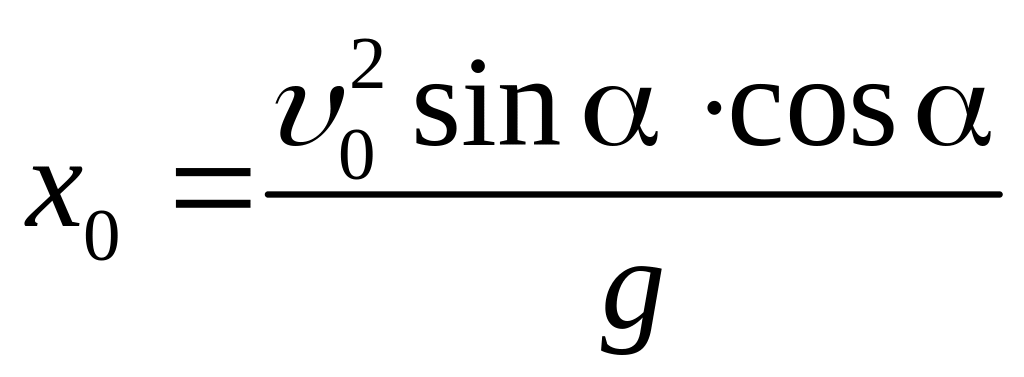
Подставив х₀ в (12), найдём высоту: